La Integral
Técnica y Método
1.9. Integración por fracciones parciales
Este método se aplica cuando la integral se hace respecto a una función racional:
![]()
Donde ![]() representan polinomios, de manera tal que
representan polinomios, de manera tal que ![]() tiene grado menor que
tiene grado menor que ![]() .
.
En este método de integración se presentan varios casos.
Caso I. El denominador tiene únicamente factores de primer grado y no se repiten.
Esto permite que a cada factor le corresponda una fracción parcial como se indica:
![]()
lo que implica que la constante ![]() debe determinarse.
debe determinarse.
1. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finalmente:
![]()
Caso II. El denominador tiene únicamente factores de primer grado y algunos se repiten.
En este caso si se tiene un factor de la forma:
![]()
Se lleva a cabo una suma desarrollada de la siguiente forma:
![]()
De manera que habrá que determinar todas las constantes: ![]()
3. ![]()
Observando el denominador, se concluye que hay tres veces el mismo denominador:
![]()
Entonces se debe desarrollar una suma como sigue:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Se concluye que:
![]()
4. ![]()
Al factorizar el denominador se observa que el factor ![]() , es repetible:
, es repetible:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Por lo tanto:
![]()
Caso III. El denominador tiene factores de segundo grado y ninguno se repite.
En este caso se considera que para un factor de la forma: ![]() se le asocie una
se le asocie una
fracción con la forma:
![]()
Así, en cada fracción será necesario determinar las constantes: ![]()
5. ![]()
Al factorizar el denominador del integrando tenemos:
![]()
Lo que resulta en un factor lineal ![]() y en un factor cuadrático
y en un factor cuadrático ![]() , el cual no se puede
, el cual no se puede
factorizar nuevamente. Por lo tanto las fracciones parciales serán:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finalmente:
![]()
6. ![]()
Se puede observar que el término cuadrático no se puede factorizar, por lo cual,
las fracciones parciales correspondientes serán:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Aplicar la fórmula (19)
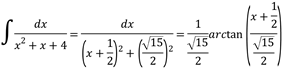
![]()
Sustituyendo en el resultado parcial obtenido:
![]()
![]()
Finalmente el resultado es:
![]()
Caso IV. El denominador tiene solo factores de segundo grado y algunos se repiten.
Cuando se tiene un factor cuadrático de la forma.
![]()
Las fracciones parciales se obtienen de una suma desarrollada de la forma:
![]()
Teniendo que determinar las constantes: ![]()
7. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finalmente el resultado queda así:
![]()
8. ![]()
Se observa que el término cuadrático es repetible, por lo que empleando fracciones
parciales, se tiene:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finalmente el resultado es:
![]()
Autores:
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Lizbeth Guadalupe Villalon Magallan
Mónica Rico Reyes
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán