Texto universitario

_____________________________
Módulo 2. Pensamiento estadístico
2.1 ¿Qué es el pensamiento estadístico?
El pensamiento estadístico se refiere a un amplio conjunto de herramientas para comprender los datos. Estas herramientas pueden clasificarse como supervisadas o no supervisadas. En términos generales, el pensamiento estadístico supervisado implica la construcción de un modelo estadístico para predecir o estimar un producto basado en una o más entradas. Problemas de esta naturaleza ocurren en campos tan diversos como negocios, medicina, astrofísica y políticas públicas. Con el pensamiento estadístico no supervisado, hay entradas pero no salidas de supervisión; sin embargo, podemos aprender las relaciones y la estructura de dichos datos. Para proporcionar una ilustración de algunas aplicaciones del pensamiento estadístico, hemos de discutir brevemente la naturaleza de los conjuntos de datos del mundo real que se consideran en este texto como esenciales para la formación del pensamiento estadístico.
Aunque el término pensamiento estadístico es bastante nuevo, muchos de los conceptos que subyacen en el campo, se desarrollaron hace mucho tiempo. A principios del siglo XIX, Legendre y Gauss publicaron artículos sobre el método de los mínimos cuadrados, que implementaron en la primera forma de lo que ahora se conoce como regresión lineal. El enfoque se aplicó por primera vez con éxito a problemas en astronomía. La regresión lineal se usa para predecir valores cuantitativos, como el salario de un individuo o el resultado de una política pública. Para predecir valores cualitativos, como si un paciente sobrevive o muere, o si el mercado de valores aumenta o disminuye, Fisher propuso un análisis discriminante lineal en 1936. En la década de 1940, varios autores presentaron un enfoque alternativo, la regresión de casos especiales como la logística[1].
A principios de la década de 1970, Nelder y Wedderburn acuñaron el término modelos lineales generalizados para toda clase de métodos de pensamiento estadístico, que incluyen tanto la regresión lineal como la logística para casos especiales[2]. A fines de la década de 1970, se disponía de más técnicas para aprender de los datos. Sin embargo, eran métodos casi exclusivamente lineales, porque el ajuste de relaciones no lineales era computacionalmente inviable en ese momento. En la década de 1980, la tecnología informática finalmente había mejorado lo suficiente como para que los métodos no lineales ya no fueran computacionalmente prohibitivos. A mediados de la década de 1980, Breiman, Friedman, Olshen y Stone introdujeron árboles de clasificación y regresión[3], y fueron de los primeros en demostrar el poder de una implementación práctica detallada de un método, incluida la validación cruzada para la selección de modelos. Hastie y Tibshirani acuñaron el término de modelos aditivos generalizados en 1986 para una clase de extensiones no lineales a modelos lineales generalizados, y también proporcionaron una implementación práctica de software[4].
Desde ese momento, inspirado en el advenimiento del aprendizaje automático y otras disciplinas, el pensamiento estadístico se ha convertido en un nuevo subcampo en estadística, centrado en el modelado y la predicción supervisada ??y no supervisada. En los últimos años, el progreso en el pensamiento estadístico ha estado marcado por la creciente disponibilidad de software potente y relativamente fácil de usar, como el popular y gratuito sistema R. Esto tiene el potencial de continuar la transformación del campo de un conjunto de técnicas utilizadas y desarrolladas por estadísticos e informáticos a un juego de herramientas esencial para una comunidad mucho más amplia de científicos, artistas, ingenieros y diseñadores.
Desde entonces, se ha convertido en una referencia importante sobre los fundamentos del pensamiento estadístico. Su éxito se deriva de su tratamiento integral y detallado de muchos temas importantes en lo estadístico, así como del hecho de que (en relación con muchos libros de texto de estadísticas de nivel superior) es accesible para una amplia audiencia. Sin embargo, el factor más importante detrás del éxito del sistema R ha sido su naturaleza de actualidad en el momento de su publicación e interés en el campo de la estadística.
El aprendizaje proporcionó una de las primeras introducciones accesibles y completas del tema. El campo del pensamiento estadístico ha seguido floreciendo. La expansión del campo ha tomado dos formas. El crecimiento más obvio ha consistido en el desarrollo de enfoques nuevos y mejorados de inferencia estadística destinados a responder una variedad de preguntas científicas en varios campos. Sin embargo, el campo estadístico también ha ampliado su audiencia en las universidades. En la década de 1990, los aumentos en el poder computacional generaron un gran interés en el campo por parte de los no estadísticos que estaban ansiosos por usar herramientas estadísticas de vanguardia para analizar sus datos. Desafortunadamente, la naturaleza altamente técnica de estos enfoques significó que la comunidad de usuarios permaneció principalmente restringida a expertos en estadística, informática y campos relacionados con la capacitación (y el tiempo de estudios de posgrado) para comprenderlos e implementarlos.
En los últimos años, los paquetes de software nuevos y mejorados han aliviado significativamente la carga de implementación de muchos métodos de pensamiento estadístico. Al mismo tiempo, ha habido un reconocimiento creciente en varios campos, desde los negocios hasta la atención médica, desde la genética hasta las ciencias sociales y más, y es que el pensamiento estadístico es una herramienta poderosa con importantes aplicaciones prácticas. Como resultado, ese campo se ha movido de un interés principalmente académico, a uno disciplinar convencional, con una enorme audiencia potencial.
Esta tendencia seguramente continuará con la creciente disponibilidad de enormes cantidades de datos y el software para analizarlos. Muchos métodos de pensamiento estadístico son relevantes y útiles en una amplia gama de disciplinas académicas y no académicas, más allá de las ciencias estadísticas. Se considera que muchos procedimientos contemporáneos estadísticos deberían, y estarán, tan ampliamente disponibles y utilizados como es el caso actualmente para métodos clásicos como la regresión lineal.
El pensamiento estadístico no debe verse como una serie de cuadros negros. Ningún enfoque único funcionará bien en todas las aplicaciones posibles. Sin comprender todos los engranajes dentro del marco conceptual, o la interacción entre esos engranajes, es imposible seleccionar el mejor cuadro de herramientas. Por lo tanto, se ha de intentar describir cuidadosamente el modelo, la intuición, los supuestos y las compensaciones detrás de cada uno de los métodos que consideramos.
Si bien, es importante saber qué trabajo realiza cada herramienta ¡no es necesario tener las habilidades para construir la máquina dentro de la caja! Por lo tanto, hemos minimizado la discusión de detalles técnicos relacionados con los procedimientos de ajuste y las propiedades teóricas. Asumimos que el lector se siente cómodo con los conceptos matemáticos básicos.
Suponemos que el lector está interesado en aplicar métodos estadísticos a problemas del mundo real. Para facilitar esto, así como para motivar las técnicas discutidas, hemos dedicado algo de espacio al laboratorio de computación R. En cada práctica, guiamos al lector a través de una aplicación realista de los métodos considerados.
Muchos de los estudiantes menos orientados a la computación que inicialmente se sintieron intimidados por la interfaz de nivel de comando de R, se acostumbraron durante el paso del curso. Hemos utilizado R porque está disponible gratuitamente y es lo suficientemente potente como para implementar todos los métodos discutidos en el curso. También tiene paquetes opcionales que se pueden descargar para implementar literalmente miles de métodos adicionales. Lo más importante es que R es el lenguaje elegido por los estadísticos académicos, y los nuevos enfoques a menudo están disponibles en R antes de que se implementen en paquetes comerciales. Sin embargo, los laboratorios pueden omitirse si el lector desea utilizar un paquete de software diferente o no desea aplicar los métodos discutidos a problemas del mundo real.
Para motivar nuestro estudio del pensamiento estadístico, comenzamos con un ejemplo simple. Supongamos que somos consultores estadísticos contratados por un cliente para brindar asesoramiento sobre cómo mejorar las ventas de un producto en particular. El conjunto de datos publicitarios consiste en las ventas de ese producto en 200 mercados diferentes, junto con presupuestos publicitarios para el producto en cada uno de esos mercados para tres medios diferentes: TV, radio y periódico. Los datos se muestran en la Figura 2.1. Nuestro cliente no puede aumentar directamente las ventas del producto. Por otro lado, pueden controlar el gasto publicitario en cada uno de los tres medios. Por lo tanto, si determinamos que existe una asociación entre publicidad y ventas, entonces podemos instruir a nuestro cliente para que ajuste los presupuestos publicitarios, aumentando indirectamente las ventas.
En otras palabras, nuestro objetivo es desarrollar un modelo preciso que pueda usarse para predecir las ventas sobre la base de los tres presupuestos de medios.
De manera más general, supongamos que observamos una respuesta cuantitativa Y y predictores diferentes, X1, X2,…, Xp. Suponemos que hay alguna relación entre Y y X = (X1, X2,..., Xp), que se puede escribir en forma muy general:
![]()
Aquí f es alguna función fija pero desconocida de X1,.., Xp, y es aleatoria, independiente de X, y tiene una media cero. En esta formulación, f representa la información sistemática que X proporciona sobre Y.
 18.46.45.png)
Figura 2.1 Conjunto de datos publicitarios.
En otro ejemplo, considere el panel de la izquierda de la figura 2.2, una gráfica de ingresos versus años de educación para 30 personas en el conjunto de datos de ingresos. La trama sugiere que uno podría predecir ingresos usando años de educación. Sin embargo, la función f que conecta la variable de entrada a la variable de salida es en general desconocida. En esta situación, uno debe estimar f con base en los puntos observados. Dado que ingresos es un conjunto de datos simulados, se conoce f y se muestra mediante la curva azul en el panel de la derecha de la figura 2.2.
 18.52.14.png)
Figura 2.2 Conjunto de datos de ingresos.
Las líneas verticales representan los términos de error. Notamos que algunas de las 30 observaciones se encuentran sobre la curva azul y algunas se encuentran debajo de ella; en general, los errores tienen aproximadamente promedio cero. De lo que puede inferirse la función f puede involucrar más de una variable de entrada. En la figura 2.3, graficamos el ingreso en función de los años de educación y antigüedad. Aquí f es una superficie bidimensional que debe estimarse con base en los datos observados.
En esencia, el pensamiento estadístico se refiere a un conjunto de enfoques para estimar f. ¿Por qué estimar f? Hay dos razones principales por las que podemos desear estimar f: predicción e inferencia. Discutimos cada una en su turno.
 18.54.24.png)
Figura 2.3 El gráfico muestra los ingresos en función de los años de educación y antigüedad en el conjunto de datos de ingresos.
Predicción. En muchas situaciones, un conjunto de entradas X está fácilmente disponible, pero la salida Y no se puede obtener fácilmente. En esta configuración, dado que el término de error promedia a cero 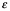 , podemos predecir Y usando:
, podemos predecir Y usando:
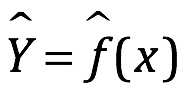
donde 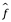 representa nuestra estimación para f, y
representa nuestra estimación para f, y 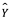 representa la predicción resultante para Y. En este contexto,
representa la predicción resultante para Y. En este contexto, a menudo se trata como una caja negra, en el sentido de que a uno no le preocupa la forma exacta de
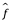 , siempre que produzca predicciones precisas para Y.
, siempre que produzca predicciones precisas para Y.
Como ejemplo, supongamos que X1 ,..., Xp son características de la muestra de sangre de un paciente que se pueden medir fácilmente en un laboratorio, Y es una variable que codifica el riesgo del paciente de una reacción adversa grave a un medicamento en particular. Es natural tratar de predecir Y usando X, ya que podemos evitar administrar el medicamento en cuestión a pacientes con alto riesgo de una reacción adversa, es decir, pacientes para quienes la estimación de Y es alta.
La precisión de 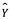 como predicción para Y depende de dos cantidades, que llamaremos error reducible y error irreducible. En general,
como predicción para Y depende de dos cantidades, que llamaremos error reducible y error irreducible. En general, 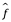 no será una estimación perfecta para f, y esta inexactitud introducirá algún error. Este error es reducible porque potencialmente podemos mejorar la precisión de
no será una estimación perfecta para f, y esta inexactitud introducirá algún error. Este error es reducible porque potencialmente podemos mejorar la precisión de 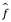 utilizando la técnica estadística más apropiada para estimar f. Sin embargo, incluso si fuera posible formar una estimación perfecta para f, de modo que nuestra respuesta estimada tomara la forma
utilizando la técnica estadística más apropiada para estimar f. Sin embargo, incluso si fuera posible formar una estimación perfecta para f, de modo que nuestra respuesta estimada tomara la forma 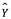 = f (X), ¡nuestra predicción aún tendría algún error! Esto se debe a que Y también es una función de
= f (X), ¡nuestra predicción aún tendría algún error! Esto se debe a que Y también es una función de 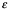 , que, por definición, no se puede predecir usando X. Por lo tanto, la variabilidad asociada también afecta la precisión de nuestras predicciones. Esto se conoce como el error irreducible o error residual, porque no importa qué tan bien estimamos f, no podemos reducir el error introducido por
, que, por definición, no se puede predecir usando X. Por lo tanto, la variabilidad asociada también afecta la precisión de nuestras predicciones. Esto se conoce como el error irreducible o error residual, porque no importa qué tan bien estimamos f, no podemos reducir el error introducido por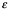 .
.
¿Por qué el error irreducible es mayor que cero? La cantidad puede contener variables no medidas que son útiles para predecir Y: dado que no las medimos, f no puede usarlas para su predicción. La cantidad también puede contener una variación inconmensurable. Por ejemplo, el riesgo de una reacción adversa puede variar para un paciente determinado en un día determinado, según la variación de fabricación del medicamento en sí o la sensación general de bienestar del paciente en ese día.
Considere una estimación dada 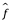 y un conjunto de predictores X, que produce la predicción
y un conjunto de predictores X, que produce la predicción 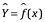 . Suponga por un momento que tanto
. Suponga por un momento que tanto 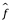 como X son fijos. Entonces, es fácil demostrar que
como X son fijos. Entonces, es fácil demostrar que
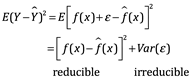
Donde 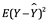 representa el promedio, o valor esperado, del cuadrado de la diferencia de la predicción y el valor actual de Y, y
representa el promedio, o valor esperado, del cuadrado de la diferencia de la predicción y el valor actual de Y, y 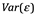 .
.
El enfoque de este curso está en las técnicas para estimar f con el objetivo de minimizar el error reducible. Es importante tener en cuenta que el error irreducible siempre proporcionará un límite superior en la precisión de nuestra predicción para Y. Este límite es casi siempre desconocido en la práctica.
Inferencia. A menudo nos interesa entender la forma en que Y se ve afectado como cambio de X1,…, Xp. En esta situación, deseamos estimar f, pero nuestro objetivo no es necesariamente hacer predicciones para Y. En cambio, queremos entender la relación entre X y Y, o más específicamente, entender cómo Y cambia en función de X1,. . ., Xp. Ahora 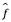 no puede ser tratado como una caja negra, porque necesitamos saber su forma exacta. En esta configuración, uno puede estar interesado en responder las siguientes preguntas:
no puede ser tratado como una caja negra, porque necesitamos saber su forma exacta. En esta configuración, uno puede estar interesado en responder las siguientes preguntas:
1. ¿Qué predictores están asociados con la respuesta? A menudo se da el caso de que solo una pequeña fracción de los predictores disponibles están sustancialmente asociados con Y. Identificar los pocos predictores importantes entre un gran conjunto de posibles variables puede ser extremadamente útil, dependiendo de la aplicación.
2. ¿Cuál es la relación entre la respuesta y cada predictor? Algunos predictores pueden tener una relación positiva con Y, en el sentido de que aumentar el predictor está asociado con valores crecientes de Y. Otros predictores pueden tener la relación opuesta. Dependiendo de la complejidad de f, la relación entre la respuesta y un predictor dado también puede depender de los valores de los otros predictores.
3. ¿Se puede resumir adecuadamente la relación entre Y y cada predictor utilizando una ecuación lineal, o la relación es más complicada? Históricamente, la mayoría de los métodos para estimar f han tomado una forma lineal. En algunas situaciones, tal suposición es razonable o incluso deseable. Pero a menudo la relación verdadera es más complicada, en cuyo caso un modelo lineal puede no proporcionar una representación precisa de la relación entre las variables de entrada y salida.
Por ejemplo, considere una empresa que esté interesada en realizar una campaña de marketing directo. El objetivo es identificar a las personas que responderán positivamente a un envío de correo, basándose en observaciones de variables demográficas medidas en cada individuo. En este caso, las variables demográficas sirven como predictores, y la respuesta a la campaña de marketing (ya sea positiva o negativa) sirve como resultado. La compañía no está interesada en obtener una comprensión profunda de las relaciones entre cada predictor individual y la respuesta; en cambio, la compañía simplemente quiere un modelo preciso para predecir la respuesta utilizando los predictores. Este es un ejemplo de modelado para predicción.
Esta situación cae dentro del paradigma de inferencia. Otro ejemplo consiste en modelar la marca de un producto que un cliente podría comprar en función de variables como el precio, la ubicación de la tienda, los niveles de descuento, el precio de la competencia, etc. En esta situación, uno podría estar realmente más interesado en cómo cada una de las variables individuales afecta la probabilidad de compra. Por ejemplo, ¿qué efecto tendrá el cambio del precio de un producto en las ventas? Este es un ejemplo de modelado por inferencia.
Finalmente, se podrían realizar algunos modelos para predicción e inferencia. Por ejemplo, en un entorno inmobiliario, uno puede buscar relacionar los valores de las viviendas con datos como la tasa de criminalidad, la zonificación, la distancia a un río, la calidad del aire, las escuelas, el nivel de ingresos de la comunidad, el tamaño de las casas, etc. En este caso, uno podría estar interesado en cómo las variables de entrada individuales afectan los precios, es decir, ¿cuánto más valdrá una casa si tiene una vista del río? Este es un problema de inferencia. Alternativamente, uno simplemente puede estar interesado en predecir el valor de una casa dadas sus características: ¿está la casa subvalorada o sobrevalorada? Este es un problema de predicción.
Dependiendo de si nuestro objetivo final es la predicción, la inferencia o una combinación de los dos, diferentes métodos para estimar f pueden ser apropiados. Por ejemplo, los modelos lineales permiten la inferencia predecible de modelos relativamente simples e interlineales, pero pueden no producir predicciones tan precisas como algunos otros enfoques. Por el contrario, algunos de los enfoques altamente no lineales pueden proporcionar predicciones bastante precisas para Y, pero esto se produce a expensas de un modelo menos interpretable para el que la inferencia es más difícil.
2.2 ¿Cómo estimamos f?
A lo largo de este texto, exploramos enfoques lineales y no lineales para estimar f. Sin embargo, estos métodos generalmente comparten ciertas características. Proporcionamos una descripción general de estas características compartidas aquí. Siempre asumiremos que hemos observado un conjunto de n puntos de datos diferentes. Por ejemplo, en la figura 2.2 observamos n=30 puntos de datos. Estas observaciones se llaman datos de entrenamiento porque usaremos estas observaciones para entrenar o enseñar a nuestro método cómo estimar f. Supongamos que xij representa el valor del jth predictor, o input, para la observación i, donde i = 1, 2,..., n y j = 1, 2,..., p. En consecuencia, deje que yi represente la variable de respuesta para la i-ésima observación. Entonces nuestros datos de entrenamiento consisten en {(x1, y1), (x2, y2),…, (xn, yn)} donde xi = (xi1, xi2,..., xip)T. Nuestro objetivo es aplicar un método de pensamiento estadístico a los datos de entrenamiento para estimar la función desconocida f. En otras palabras, queremos encontrar una función 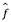 tal que
tal que 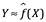 para cualquier observación (X, Y). En términos generales, la mayoría de los métodos de pensamiento estadístico para esta tarea pueden caracterizarse como paramétricos o no paramétricos. Ahora discutimos brevemente estos dos tipos de enfoques.
para cualquier observación (X, Y). En términos generales, la mayoría de los métodos de pensamiento estadístico para esta tarea pueden caracterizarse como paramétricos o no paramétricos. Ahora discutimos brevemente estos dos tipos de enfoques.
Métodos paramétricos
Los métodos paramétricos implican un enfoque basado en modelos de dos pasos.
1. Primero, hacemos una suposición sobre la forma funcional, o forma de f. Por ejemplo, una suposición muy simple es que f es lineal en X:
f (X) = β0 + β1X1 + β2X2 + . . . + βpXp
Este es un modelo lineal. Una vez que hemos asumido que f es lineal, el problema de estimar f se simplifica enormemente. En lugar de tener que estimar una función p-dimensional completamente arbitraria f (X), uno solo necesita estimar los coeficientes p+1 de β0, β1,... βp.
2. Después de seleccionar un modelo, necesitamos un procedimiento que use los datos de entrenamiento para ajustarlo o entrenarlo. En el caso para el modelo lineal necesitamos estimar los parámetros β0, β1,. . . βp. Es decir, queremos encontrar valores de estos parámetros de manera que
Y ≈ β0 + β1X1 + β2X2 +. . . + βpXp
Se hace referencia al enfoque más común para ajustar el modelo como mínimos cuadrados (ordinarios). Sin embargo, los mínimos cuadrados es una de las muchas formas posibles de ajustar el modelo lineal.
El enfoque basado en el modelo recién descrito se conoce como paramétrico; reduce el problema de estimar f a uno de estimar un conjunto de parámetros. Asumir una forma paramétrica para f simplifica el problema de estimar f, porque generalmente es mucho más fácil estimar un conjunto de parámetros, como β0, β1,…, βp en el modelo lineal (2.4), que corresponde a una función completamente arbitraria f. La desventaja potencial de un enfoque paramétrico es que el modelo que elegimos generalmente no coincidirá con la verdadera forma desconocida de f. Si el modelo elegido está demasiado lejos de la verdadera f, entonces nuestra estimación será pobre. Podemos tratar de abordar este problema eligiendo modelos flexibles que puedan adaptarse a muchas formas funcionales posibles diferentes para f. Pero en general, ajustar un modelo más flexible requiere estimar un mayor número de parámetros. Estos modelos más complejos pueden conducir a un fenómeno conocido como sobre ajustar los datos, lo que esencialmente significa que siguen los errores, o el ruido, demasiado de cerca.
La figura 2.4 muestra un ejemplo del enfoque paramétrico aplicado a los datos de ingresos de la figura 2.3. Hemos ajustado un modelo lineal de la forma
income ≈ β0 + β1 ~ education+ β2 ~ seniority.
 10.51.09.png)
Figura 2.4. Un modelo lineal.
Como hemos asumido una relación lineal entre la respuesta y los dos predictores, todo el problema de ajuste se reduce a la estimación de β0, β1 y β2, lo que hacemos utilizando regresión lineal de mínimos cuadrados. Comparando la figura 2.3 con la figura 2.4, podemos ver que el ajuste lineal dado en la figura 2.4 no es del todo correcto: la verdadera f tiene cierta curvatura que no se captura en el ajuste lineal. Sin embargo, el ajuste lineal todavía parece hacer un trabajo razonable al capturar la relación positiva entre años de educación e ingresos, así como la relación ligeramente menos positiva entre antigüedad e ingresos. Puede ser que con un número tan pequeño de observaciones, esto sea lo mejor que podemos hacer.
2.3 Métodos no paramétricos
Los métodos no paramétricos no hacen suposiciones explícitas sobre la forma funcional de f. En su lugar, buscan una estimación de f que se acerque lo más posible a los puntos de datos sin ser demasiado tosco u ondulado. Tales enfoques pueden tener una gran ventaja sobre los enfoques paramétricos: al evitar la suposición de una forma funcional particular para f, tienen el potencial de ajustar con precisión un rango más amplio de formas posibles para f. Cualquier enfoque paramétrico conlleva la posibilidad de que la forma funcional utilizada para estimar f sea muy diferente de la verdadera f, en cuyo caso el modelo resultante no se ajustará bien a los datos. Por el contrario, los enfoques no paramétricos evitan por completo este peligro, ya que esencialmente no se asume la forma de f. Pero los enfoques no paramétricos tienen una gran desventaja: dado que no reducen el problema de estimar f a un pequeño número de parámetros, un gran número de observaciones (mucho más de lo que normalmente se necesita para un enfoque paramétrico) es necesario para obtener una estimación precisa de f. En la figura 2.5 se muestra un ejemplo de un enfoque no paramétrico para ajustar los datos de ingresos. Se usa una estría de placa delgada para estimar f.
 10.57.54.png)
Figura 2.5. Una estría de placa delgada y lisa que se ajusta a los datos de ingresos de la figura 2.3 se muestra en amarillo; las observaciones se muestran en rojo.
Este enfoque no impone ningún modelo especificado previamente en f. En su lugar, intenta producir una estimación para f que esté lo más cerca posible de los datos observados, sujeto al ajuste, es decir, la superficie amarilla en la figura 2.5, que sea suave. En este caso, el ajuste no paramétrico ha producido una estimación notablemente precisa de la verdadera f que se muestra en la figura 2.3. Para ajustarse a una ranura de placa delgada, el analista de datos debe seleccionar un nivel de suavidad. La figura 2.6 muestra el mismo ajuste de ranura de placa delgada usando un nivel más bajo de suavidad, lo que permite un ajuste más rugoso. ¡La estimación resultante se ajusta perfectamente a los datos observados!
Sin embargo, el ajuste de ranura que se muestra en la figura 2.6 es mucho más variable que la verdadera función f, de la figura 2.3. Este es un ejemplo de sobre ajuste de los datos, que discutimos anteriormente. Es una situación indeseable porque el ajuste obtenido no arrojará estimaciones precisas de la respuesta en nuevas observaciones que no formaron parte del conjunto de datos de entrenamiento original. Como hemos visto, hay ventajas y desventajas en los métodos paramétricos y no paramétricos para el pensamiento estadístico.
 08.58.53.png)
Figura 2.6. Una estría áspera de placa delgada se ajusta a los datos de ingresos de la figura 2.3. Este ajuste no produce errores en los datos de entrenamiento.
La compensación entre la precisión de predicción y el modelo de interpretabilidad predictivo
De los muchos métodos, algunos son menos flexibles o más restrictivos, en el sentido de que pueden producir un rango relativamente pequeño de formas para estimar f. Por ejemplo, la regresión lineal es un enfoque relativamente inflexible, porque solo puede generar funciones lineales como las líneas que se muestran en la figura 2.1 o el plano que se muestra en la figura 2.4. Otros métodos, como las estrías de placas delgadas que se muestran en las figuras 2.5 y 2.6, son considerablemente más flexibles porque pueden generar un rango mucho más amplio de formas posibles para estimar f.
Razonablemente se podría hacer la siguiente pregunta: ¿por qué elegiríamos utilizar un método más restrictivo en lugar de un enfoque muy flexible? Hay varias razones por las que preferiríamos un modelo más restrictivo. Si estamos interesados principalmente en la inferencia, los modelos restrictivos son más interpretables. Por ejemplo, cuando el objetivo es la inferencia, el modelo lineal puede ser una buena opción ya que será bastante fácil entender la relación entre Y y X1, X2, ..., Xp.
 08.59.21.png)
Figura 2.7. Una representación de la compensación entre flexibilidad e interpretabilidad, utilizando diferentes métodos de aprendizaje estadístico. En general, a medida que aumenta la flexibilidad de un método, disminuye su interpretabilidad.
La figura 2.7 proporciona una ilustración de la compensación entre flexibilidad e interpretabilidad para algunos de los métodos que cubrimos en este texto. La regresión lineal de mínimos cuadrados, es relativamente inflexible pero es bastante interpretable, esta es basa en el modelo lineal (2.4) pero utiliza un procedimiento de ajuste alternativo para estimar los coeficientes β0, β1,..., Βp. El nuevo procedimiento es más restrictivo al estimar los coeficientes, y establecer un número de ellos exactamente en cero. En este sentido, el lazo es un enfoque menos flexible que la regresión lineal. También es más interpretable que la regresión lineal, porque en el modelo final la variable de respuesta solo estará relacionada con un pequeño subconjunto de predictores, es decir, aquellos con estimaciones de coeficientes distintos de cero.
Los modelos aditivos generalizados (GAM), en su lugar extienden el modelo lineal (2.4) para permitir ciertas relaciones no lineales. En consecuencia, los GAM son más flexibles que la regresión lineal. También son algo menos interpretables que la regresión lineal, porque la relación entre cada predictor y la respuesta ahora se modela utilizando una curva. Finalmente, los métodos completamente no lineales como el embolsado, refuerzo y máquinas de vectores de soporte con núcleos no lineales, son enfoques altamente flexibles que son más difíciles de interpretar.
Hemos establecido que cuando la meta es la inferencia, existen claras ventajas de usar métodos de pensamiento estadístico simple y relativamente inflexible. Sin embargo, en algunos entornos, solo estamos interesados ??en la predicción, y la interpretabilidad del modelo predictivo simplemente no es de interés. Por ejemplo, si buscamos desarrollar un algoritmo para predecir el precio de una acción, nuestro único requisito para el algoritmo es que prediga con precisión: la interpretabilidad no es una preocupación. En este contexto, podríamos esperar que sea mejor usar el modelo más flexible disponible. Sorprendentemente, ¡este no es siempre el caso! A menudo obtendremos predicciones más precisas utilizando un método menos flexible. Este fenómeno, que puede parecer contradictorio a primera vista, tiene que ver con el potencial de sobreajuste en sistemas altamente flexibles de métodos. Vimos un ejemplo de sobreajuste en la figura 2.6.
2.4 Pensamiento supervisado versus no supervisado
La mayoría de los problemas de pensamiento estadístico se dividen en una de dos categorías: supervisados ??o no supervisados. Los ejemplos que hemos discutido hasta ahora caen en el dominio de pensamiento supervisado. Por cada observación de las mediciones del predictor xi, i = 1,…, n hay una medida de respuesta asociada yi. Deseamos ajustar un modelo que relacione la respuesta con los predictores, con el objetivo de predecir con precisión la respuesta para futuras observaciones (predicción) o comprender mejor la relación entre la respuesta y los predictores (inferencia). Muchos métodos clásicos de aprendizaje estadístico, como la regresión lineal y la regresión logística, así como enfoques más modernos como GAM, máquinas de vectores de apoyo y de refuerzo, operan en el dominio de aprendizaje supervisado.
Por el contrario, el aprendizaje no supervisado describe la situación un tanto más desafiante en la que para cada observación i = 1,..., n, observamos un vector de mediciones xi pero ninguna respuesta asociada yi. No es posible ajustar un modelo de regresión lineal, dado que no hay una variable de respuesta para predecir. En este contexto, en cierto sentido estamos trabajando ciegos; la situación se conoce como no supervisada porque carecemos de una variable de respuesta que pueda supervisar nuestro análisis. ¿Qué tipo de análisis estadístico es posible? tratar de comprender las relaciones entre las variables o entre las observaciones. Una herramienta de pensamiento estadístico que podemos utilizar en este contexto es el análisis de conglomerados, o agrupamiento. El objetivo del análisis de conglomerados es determinar, sobre la base de x1,…, xn, si las observaciones se dividen en grupos relativamente distintos. Por ejemplo, en un estudio de segmentación de mercado podríamos observar múltiples características (variables) para clientes potenciales, como código postal, familia ingresos y hábitos de compra. Podríamos creer que los clientes se dividen en diferentes grupos, como los que gastan mucho en comparación con los que gastan poco. Si la información sobre los patrones de gasto de cada cliente estuviera disponible, entonces sería posible un análisis supervisado. Sin embargo, esta información no es disponible, es decir, no sabemos si cada cliente potencial gasta mucho o no. En este contexto, podemos intentar agrupar a los clientes en función de las variables medidas para identificar grupos distintos de clientes potenciales. Tales grupos pueden ser de interés porque podría ser que los grupos difieren con respecto a alguna propiedad de interés, como los hábitos de gasto.
 11.10.23.png)
Figura 2.8. Un conjunto de datos de agrupación que involucra tres grupos. Cada grupo se muestra con un símbolo de color diferente. Izquierda: los tres grupos están bien separados. En esta configuración, un enfoque de agrupación debe identificar con éxito los tres grupos. Derecha: hay alguna superposición entre los grupos. Ahora la tarea de agrupamiento es más desafiante.
La figura 2.8 proporciona una ilustración simple del problema de agrupamiento. Hemos trazado 150 observaciones con medidas en dos variables, X1 y X2. Cada observación corresponde a uno de tres grupos distintos. Para fines ilustrativos, hemos trazado los miembros de cada grupo usando diferentes colores y símbolos. Sin embargo, en la práctica se desconocen los miembros del grupo, y el objetivo es determinar el grupo al que pertenece cada observación. En el panel izquierdo de la figura 2.8, esta es una tarea relativamente fácil porque los grupos están en diferentes posiciones, el panel de la derecha ilustra un problema más desafiante en el que hay cierta superposición entre los grupos. No se puede esperar que un método de agrupamiento asigne todos los puntos superpuestos a su grupo correcto (azul, verde o naranja).
En los ejemplos que se muestran en la figura 2.8, solo hay dos variables, por lo que uno simplemente puede inspeccionar visualmente los diagramas de dispersión de las observaciones para identificar los grupos, sin embargo, en la práctica, a menudo encontramos conjuntos de datos que contienen muchas más de dos variables. En este caso, no podemos trazar fácilmente las observaciones. Por ejemplo, si hay variables p en nuestro conjunto de datos, entonces se pueden hacer p (p - 1) / 2 diagramas de dispersión distintos, y la inspección visual simplemente no es una forma viable de identificar agrupaciones. Por esta razón, los métodos de agrupación automatizados son importantes.
Muchos problemas caen naturalmente en los paradigmas de pensamiento supervisados ??o no supervisado. Sin embargo, a veces la cuestión de si un análisis debe considerarse supervisado o no es menos clara. Por ejemplo, supongamos que tenemos un conjunto de n observaciones, donde m<n, tenemos tanto medidas de predicción como una medida de respuesta. Para las restantes observaciones de n = m, tenemos medidas de predicción pero no medida de respuesta. Tal escenario puede surgir si los predictores pueden medirse de manera relativamente barata pero para el correspondiente las respuestas son mucho más caras de recopilar. Nos referimos a esta configuración como un problema de pensamiento semi-supervisado. En esta configuración, deseamos utilizar un método de pensamiento estadístico que pueda incorporar m observaciones para las que hay medidas de respuesta disponibles, así como el n = m observaciones para las que no son. Aunque este es un tema interesante, está más allá del alcance de este texto.
2.5 Regresión versus problemas de clasificación
Las variables pueden caracterizarse como cuantitativas o cualitativas (también conocidas como categóricas). Las variables cuantitativas toman valores numéricos. Los ejemplos incluyen la edad, la altura o el ingreso de una persona, el valor de una casa y el precio de una acción. Por el contrario, las variables cualitativas toman valores en una de las diferentes clases (K) o categorías. Los ejemplos de variables cualitativas incluyen el género de una persona (hombre o mujer), la marca del producto comprado (marca A, B o C), si una persona incumple una deuda (sí o no), o un diagnóstico de cáncer (leucemia mieloblástica aguda, leucemia linfoblástica aguda o negativo para leucemia). Tendemos a referirnos a problemas con una respuesta cuantitativa como problemas de regresión, mientras que aquellos que involucran una respuesta cualitativa a menudo se denominan problemas de clasificación. Sin embargo, la distinción no siempre es tan nítida: la regresión lineal de mínimos cuadrados se usa con una respuesta cuantitativa, mientras que la regresión logística se usa típicamente con una respuesta cualitativa (dos clases o binaria), a menudo se usa como método de clasificación, pero dado que estima las probabilidades de clase, también puede considerarse como un método de regresión.
Tendemos a seleccionar métodos de aprendizaje estadístico sobre la base de si la respuesta es cuantitativa o cualitativa, es decir, podríamos usar regresión lineal cuantitativa y regresión logística cuando sea cualitativa. Sin embargo, si los predictores son cualitativos o cuantitativos generalmente se considera menos importante. Los métodos de pensamiento estadístico que se analizan en este libro se pueden aplicar independientemente del tipo de variable predictiva, siempre que los predictores cualitativos se codifiquen correctamente antes de realizar el análisis.
2.6 Evaluación de la precisión del modelo
Uno de los objetivos clave es presentar al lector una amplia gama de métodos estadísticos que se extienden mucho más allá del enfoque de regresión lineal estándar. ¿Por qué es necesario introducir tantos enfoques de aprendizaje estadístico diferentes, en lugar de solo un mejor método? No hay premio gratis en estadísticas: ningún método domina a todos los demás en todos los conjuntos de datos posibles. En un conjunto de datos en particular, un método específico puede funcionar, pero algún otro método puede funcionar mejor en un conjunto de datos similar. Por tanto, es una tarea importante decidir para cualquier conjunto de datos determinado qué método produce los mejores resultados. Seleccionar el mejor enfoque puede ser una de las partes más desafiantes de realizar del aprendizaje estadístico en la práctica.
Discutimos algunos de los conceptos más importantes que surgen al seleccionar un procedimiento estadístico para un conjunto de datos específico. A medida que avanza nuestra discusión, explicaremos cómo se pueden aplicar en la práctica los conceptos presentados aquí.
2.6.1 Medición de la calidad de ajuste
Para evaluar el rendimiento de un método estadístico en un conjunto de datos dado, necesitamos alguna forma de medir qué tan bien sus predicciones coinciden realmente con los datos observados. Es decir, necesitamos cuantificar la medida en que el valor de respuesta predicho para una observación determinada se acerca al valor de respuesta real para esa observación. En el entorno de regresión, la medida más utilizada es el error cuadrático medio (MSE), dado por:
![]()
donde 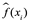 es la predicción que da
es la predicción que da 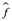 para la i-ésima observación. El MSE será pequeño si las respuestas predichas están muy cerca de las respuestas verdaderas, y será grande si para algunas de las observaciones, las respuestas predichas y verdaderas difieren sustancialmente.
para la i-ésima observación. El MSE será pequeño si las respuestas predichas están muy cerca de las respuestas verdaderas, y será grande si para algunas de las observaciones, las respuestas predichas y verdaderas difieren sustancialmente.
El MSE en 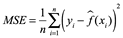 se calcula utilizando los datos de entrenamiento que se utilizaron para ajustar el modelo, por lo que debería denominarse con mayor precisión el MSE de entrenamiento. Pero, en general, no nos importa lo bien que funcione el método con los datos de entrenamiento. Más bien, estamos interesados ??en la precisión de las predicciones que obtenemos cuando aplicamos nuestro método a datos de prueba nunca antes vistos. ¿Por qué es esto lo que nos importa? Suponga que estamos interesados ??en desarrollar un algoritmo para predecir el precio de una acción en función de los rendimientos de las acciones anteriores. Podemos entrenar el método utilizando las devoluciones de acciones de los últimos 6 meses. Pero realmente no nos importa qué tan bien nuestro método predice el precio de las acciones de la semana pasada. En cambio, nos preocupamos por saber qué tan bien predecirá el precio de mañana o el precio del próximo mes. En una nota similar, suponga que tenemos mediciones clínicas (por ejemplo, peso, presión arterial, altura, edad, antecedentes familiares de enfermedad) para varios pacientes, así como información sobre si cada paciente tiene diabetes. Podemos utilizar a estos pacientes para entrenar un método de aprendizaje estadístico para predecir el riesgo de diabetes basado en mediciones clínicas. En la práctica, queremos que este método prediga con precisión el riesgo de diabetes para futuros pacientes en función de sus mediciones clínicas. No estamos muy interesados ??en si el método predice con precisión el riesgo de diabetes para los pacientes utilizados para entrenar el modelo, ya que sabemos cuáles de esos pacientes tienen diabetes.
se calcula utilizando los datos de entrenamiento que se utilizaron para ajustar el modelo, por lo que debería denominarse con mayor precisión el MSE de entrenamiento. Pero, en general, no nos importa lo bien que funcione el método con los datos de entrenamiento. Más bien, estamos interesados ??en la precisión de las predicciones que obtenemos cuando aplicamos nuestro método a datos de prueba nunca antes vistos. ¿Por qué es esto lo que nos importa? Suponga que estamos interesados ??en desarrollar un algoritmo para predecir el precio de una acción en función de los rendimientos de las acciones anteriores. Podemos entrenar el método utilizando las devoluciones de acciones de los últimos 6 meses. Pero realmente no nos importa qué tan bien nuestro método predice el precio de las acciones de la semana pasada. En cambio, nos preocupamos por saber qué tan bien predecirá el precio de mañana o el precio del próximo mes. En una nota similar, suponga que tenemos mediciones clínicas (por ejemplo, peso, presión arterial, altura, edad, antecedentes familiares de enfermedad) para varios pacientes, así como información sobre si cada paciente tiene diabetes. Podemos utilizar a estos pacientes para entrenar un método de aprendizaje estadístico para predecir el riesgo de diabetes basado en mediciones clínicas. En la práctica, queremos que este método prediga con precisión el riesgo de diabetes para futuros pacientes en función de sus mediciones clínicas. No estamos muy interesados ??en si el método predice con precisión el riesgo de diabetes para los pacientes utilizados para entrenar el modelo, ya que sabemos cuáles de esos pacientes tienen diabetes.
Para expresarlo de manera matemática, suponga que ajustamos nuestro método de aprendizaje estadístico a nuestras observaciones de entrenamiento {(x1, y1), (x2, y2),..., (xn, yn)}, y obtenemos la estimación 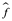 . Entonces podemos calcular
. Entonces podemos calcular 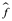 (x1),
(x1), 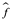 (x2),...,
(x2),..., 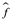 (xn).
(xn).
Si son aproximadamente iguales a y1, y2,..., yn, entonces el MSE de entrenamiento dado por 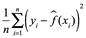 es pequeño. Sin embargo, en realidad no nos interesa si
es pequeño. Sin embargo, en realidad no nos interesa si 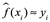 ; en su lugar, queremos saber si
; en su lugar, queremos saber si 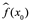 es aproximadamente igual a
es aproximadamente igual a 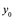 , donde (x0, y0) es una observación de prueba nunca antes vista que no se usa para entrenar el método estadístico. Queremos elegir el método que dé el MSE de prueba más bajo, a diferencia del MSE de entrenamiento más bajo. En otras palabras, si tuviéramos una gran cantidad de observaciones de prueba, podríamos calcular:
, donde (x0, y0) es una observación de prueba nunca antes vista que no se usa para entrenar el método estadístico. Queremos elegir el método que dé el MSE de prueba más bajo, a diferencia del MSE de entrenamiento más bajo. En otras palabras, si tuviéramos una gran cantidad de observaciones de prueba, podríamos calcular:
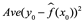
el error de predicción cuadrático medio para estas observaciones de prueba es (x0, y0). Nos gustaría seleccionar el modelo para el cual el promedio de esta cantidad (el MSE de prueba) es lo más pequeño posible.
¿Cómo podemos intentar seleccionar un método que minimice el MSE de prueba? En algunos entornos, podemos tener un conjunto de datos de prueba disponible, es decir, podemos tener acceso a un conjunto de observaciones que no se utilizaron para entrenar el método de aprendizaje estadístico. Entonces podemos simplemente evaluar 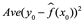 en las observaciones de la prueba y seleccionar el método de aprendizaje para el cual la prueba MSE es pequeñísimo. Pero, ¿y si no hay observaciones de prueba disponibles? En ese caso, uno podría imaginarse simplemente seleccionando un método estadístico que minimice el entrenamiento
en las observaciones de la prueba y seleccionar el método de aprendizaje para el cual la prueba MSE es pequeñísimo. Pero, ¿y si no hay observaciones de prueba disponibles? En ese caso, uno podría imaginarse simplemente seleccionando un método estadístico que minimice el entrenamiento 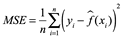 . Este parece ser un enfoque sensato, ya que el MSE de entrenamiento y el MSE de prueba parecen estar estrechamente relacionados. Desafortunadamente, hay un problema fundamental con esta estrategia: no hay garantía de que el método con el MSE de entrenamiento más bajo también tenga el MSE de prueba más bajo. En términos generales, el problema es que muchos métodos estadísticos estiman específicamente los coeficientes para minimizar el MSE del conjunto de entrenamiento. Para estos métodos, el conjunto de entrenamiento MSE puede ser bastante pequeño, pero el MSE de prueba suele ser mucho mayor.
. Este parece ser un enfoque sensato, ya que el MSE de entrenamiento y el MSE de prueba parecen estar estrechamente relacionados. Desafortunadamente, hay un problema fundamental con esta estrategia: no hay garantía de que el método con el MSE de entrenamiento más bajo también tenga el MSE de prueba más bajo. En términos generales, el problema es que muchos métodos estadísticos estiman específicamente los coeficientes para minimizar el MSE del conjunto de entrenamiento. Para estos métodos, el conjunto de entrenamiento MSE puede ser bastante pequeño, pero el MSE de prueba suele ser mucho mayor.
 16.51.39.png)
La figura 2.9 ilustra este fenómeno con un ejemplo sencillo. En el panel de la izquierda de la figura, hemos generado observaciones con la verdadera f dada por la curva negra. Las curvas naranja, azul y verde ilustran tres posibles estimaciones de f obtenidas utilizando métodos con niveles crecientes de flexibilidad. La línea naranja es el ajuste de regresión lineal, que es relativamente inflexible. Las curvas azul y verde se produjeron utilizando splines suavizados, con diferentes niveles de suavidad. Está claro que a medida que aumenta el nivel de flexibilidad, las curvas se ajustan más a los datos observados. La curva verde es la más flexible y coincide muy bien con los datos; sin embargo, observamos que se ajusta mal a la verdadera f (mostrada en negro) porque es demasiado ondulada. Al ajustar el nivel de flexibilidad del ajuste de spline suavizado, podemos producir muchos ajustes diferentes para estos datos.
Pasamos ahora al panel de la derecha de la figura 2.9. La curva gris muestra el MSE de entrenamiento promedio en función de la flexibilidad, o más formalmente los grados de libertad, para una serie de splines suavizados. Los grados de libertad son una cantidad que resume la flexibilidad de una curva. Los cuadrados naranja, azul y verde indican las MSE asociadas con las curvas correspondientes en el panel de la izquierda. Una curva más restringida y, por lo tanto, más suave tiene menos grados de libertad que una curva ondulada; observe que en la figura, la regresión lineal se encuentra en el extremo más restrictivo, con dos grados de libertad. El entrenamiento MSE declina monótonamente a medida que aumenta la flexibilidad. En este ejemplo, la verdadera f no es lineal, por lo que el ajuste lineal naranja no es lo suficientemente flexible para estimar f bien. La curva verde tiene el MSE de entrenamiento más bajo de los tres métodos, ya que corresponde a la más flexible de las tres curvas ajustadas en el panel de la izquierda. En este ejemplo, conocemos la función verdadera f, por lo que también podemos calcular la prueba MSE sobre un conjunto de pruebas muy grande, como función de la flexibilidad. (Por supuesto, en general se desconoce f, por lo que esto no será posible). El MSE de prueba se muestra usando la curva roja en el panel de la derecha de la figura. Al igual que con el MSE de entrenamiento, el MSE de prueba inicialmente disminuye a medida que aumenta el nivel de flexibilidad. Sin embargo, en algún momento la prueba MSE se estabiliza y luego comienza a aumentar nuevamente.
En consecuencia, las curvas naranja y verde tienen un MSE de prueba alto. La curva azul minimiza la prueba MSE, lo que no debería sorprender dado que visualmente parece estimar f la mejor en el panel de la izquierda de la figura. La línea discontinua horizontal indica Var (), el error irreductible en:
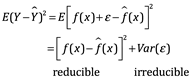
que corresponde al MSE de prueba más bajo alcanzable entre todos los métodos posibles. Por lo tanto, la spline de suavizado representada por la curva azul es casi óptima. En el panel de la derecha de la figura, a medida que aumenta la flexibilidad del método de aprendizaje estadístico, observamos una disminución monótona en el MSE de entrenamiento y una forma de U en el MSE de prueba. Esta es una propiedad fundamental del aprendizaje estadístico que se mantiene independientemente del conjunto de datos en particular y del método estadístico que se utilice. A medida que aumenta la flexibilidad del modelo, el entrenamiento MSE disminuirá, pero es posible que el MSE de prueba no. Cuando un método dado produce un MSE de entrenamiento pequeño pero un MSE de prueba grande, se dice que estamos sobreajustando los datos. Esto sucede porque nuestro procedimiento de aprendizaje estadístico está trabajando demasiado para encontrar patrones en los datos de entrenamiento y puede estar detectando algunos patrones que son causados ??por el azar en lugar de por propiedades verdaderas de la función desconocida f. Cuando sobre ajustamos los datos de entrenamiento, el MSE de prueba será muy grande porque los supuestos patrones que el método encontró en los datos de entrenamiento simplemente no existen en los datos de prueba. Tenga en cuenta que, independientemente de si se ha producido un sobreajuste o no, casi siempre esperamos que el MSE de entrenamiento sea más pequeño que el MSE de prueba porque la mayoría de los métodos estadísticos, directa o indirectamente, buscan minimizar el MSE de entrenamiento. El sobreajuste se refiere específicamente al caso en el que un modelo menos flexible habría producido un MSE de prueba más pequeño.
2.7 El desafío en el marco de la regresión
Los desafíos de la inferencia estadística tienen que ver con la generalización de la muestra a la población, un problema que se asocia con el muestreo de encuestas pero que en realidad surge en casi todas las aplicaciones de inferencia estadística. Otro desafío es la generalización del tratamiento al grupo de control, un problema que está asociado con la inferencia causal, que es implícita o explícitamente parte de la interpretación de la mayoría de las regresiones. Y el último desafío clásico, es la generalización desde las mediciones observables hasta las construcciones subyacentes de interés, ya que la mayoría de las veces nuestros datos no registran exactamente lo que nos gustaría estudiar.
Los tres desafíos se pueden enmarcar como problemas de predicción para situaciones de nuevas personas o nuevos elementos que no están en la muestra, resultados futuros bajo diferentes tratamientos potenciales asignados, y construcciones subyacentes de interés, si pudieran medirse exactamente.
Para enfrentar los desafíos debemos:
Comprender los modelos de regresión. Estos son modelos matemáticos para predecir una variable de resultado a partir de un conjunto de predictores, comenzando con ajustes en línea recta y pasando a varias generalizaciones no lineales.
- Construcción de modelos de regresión. El marco de regresión es abierto, con muchas opciones que implican la elección de qué variables incluir y cómo transformarlas y restringirlas.
- Ajustes de modelos de regresión a los datos, lo que se hace empleando software de código abierto R.
- Mostrar e interpretar los resultados, lo que requiere de habilidades de programación adicionales y comprensión matemática.
El tema central aquí, es sin duda la inferencia, es decir, el uso de modelos matemáticos para hacer afirmaciones generales a partir de datos particulares.
2.8 ¿Por qué aprender regresión?
La regresión es un método que permite a los investigadores resumir cómo las predicciones o los valores medios de un resultado varían entre individuos definidos por un conjunto de predictores. El modelo nos permite predecir por ejemplo, el voto en una elección, con cierta incertidumbre, dada la economía y bajo el supuesto de que las elecciones futuras son de alguna manera como lo fueron en el pasado.
Hagamos el cómputo en R de un ejemplo, primero cargamos los datos. Con getwd() se muestra el directorio de la carpeta de trabajo.
> getwd()
[1] "/Users/administradorcie/Documents/ALibros 2020 Prin CIE/Libro Estadistica2020"
Nosotros cargaremos el paquete rprojroot, lo que facilita la ejecución de código de diferentes subcarpetas sin necesidad de cambiar el directorio de trabajo a una carpeta específica.
Al arranque de cada sesión R:
library("rprojroot")
root<-has_dirname("ROS-Examples")$make_fix_file()
library("rstanarm")
library("arm")
library("ggplot2")
library("bayesplot")
theme_set(bayesplot::theme_default(base_family = "sans"))
Vamos a leer el archivo hibbs.dat que previamente colocamos en nuestro directorio de trabajo
hibbs <- read.table("hibbs.dat", header=TRUE)
Luego hacemos una gráfica de la dispersión:
> hibbs <- read.table("hibbs.dat", header=TRUE)
> hibbs
V1 V2 V3 V4 V5
1 year growth vote inc_party_candidate other_candidate
2 1952 2.4 44.6 Stevenson Eisenhower
3 1956 2.89 57.76 Eisenhower Stevenson
4 1960 .85 49.91 Nixon Kennedy
5 1964 4.21 61.34 Johnson Goldwater
6 1968 3.02 49.60 Humphrey Nixon
7 1972 3.62 61.79 Nixon McGovern
8 1976 1.08 48.95 Ford Carter
9 1980 -.39 44.70 Carter Reagan
10 1984 3.86 59.17 Reagan Mondale
11 1988 2.27 53.94 Bush, Sr. Dukakis
12 1992 .38 46.55 Bush, Sr. Clinton
13 1996 1.04 54.74 Clinton Dole
14 2000 2.36 50.27 Gore Bush, Jr.
15 2004 1.72 51.24 Bush, Jr. Kerry
16 2008 .1 46.32 McCain Obama
17 2012 .95 52.00 Obama Romney
plot(hibbs$growth, hibbs$vote, xlab="promedio recientes de crecimiento en personas por ingresos", ylab="Participación de votos del partido titular")
 12.56.55.png)
Enseguida construir la gráfica el “modelo de sustento y orden público”, con el código R:
________
with(hibbs, {
for (i in 1:n){
ii <- order(growth)[i]
text(left-.3, i, paste (inc[ii], " vs. ", other[ii], " (", year[ii], ")", sep=""), adj=0, cex=.8)
text(left-.3, i, paste (inc_party_candidate[ii], " vs. ", other_candidate[ii], " (", year[ii], ")", sep=""), adj=0, cex=.8)
points(center+f*(vote[ii]-50)/10, i, pch=20)
if (i>1){
if (floor(growth[ii]) != floor(growth[order(growth)[i-1]])){
lines(c(left-.3,center+.22), rep(i-.5,2), lwd=.5, col="darkgray")
}
}
}
})
lines(center+f*c(-.65,1.3), rep(0,2), lwd=.5)
for (tick in seq(-.5,1,.5)){
lines(center + f*rep(tick,2), c(0,-.2), lwd=.5)
text(center + f*tick, -.5, paste(50+10*tick,"%",sep=""), cex=.8)
}
lines(rep(center,2), c(0,n+.5), lty=2, lwd=.5)
text(center+.05, n+1.5, "Participación del partido en ejercicio en el voto popular", cex=.8)
lines(c(center-.088,center+.19), rep(n+1,2), lwd=.5)
text(right, n+1.5, "Income growth", adj=.5, cex=.8)
lines(c(right-.05,right+.05), rep(n+1,2), lwd=.5)
text(right, 16.15, "more than 4%", cex=.8)
text(right, 14, "3% to 4%", cex=.8)
text(right, 10.5, "2% to 3%", cex=.8)
text(right, 7, "1% to 2%", cex=.8)
text(right, 3.5, "0% to 1%", cex=.8)
text(right, .85, "negative", cex=.8)
text(left-.3, -2.3, "Los enfrentamientos anteriores se enumeran como candidata del partido titular vs.\ Candidata de otro partido.\nIncome el crecimiento es una medida ponderada durante los cuatro años anteriores a la elección. El voto compartido excluye a terceros.", adj=0, cex=.7)
#+ eval=FALSE, include=FALSE
if (savefigs) dev.off()
#+ eval=FALSE, include=FALSE
if (savefigs) pdf(root("ElectionsEconomy/figs","hibbsscatter.pdf"), height=4.5, width=5)
#+
par(mar=c(3,3,2,.1), mgp=c(1.7,.5,0), tck=-.01)
plot(c(-.7, 4.5), c(43,63), type="n", xlab="Promedio de crecimiento reciente en los ingresos personales", ylab="Participación de votos del partido titular", xaxt="n", yaxt="n", mgp=c(2,.5,0), main="Pronosticar la elección de la economía ", bty="l")
axis(1, 0:4, paste(0:4,"%",sep=""), mgp=c(2,.5,0))
axis(2, seq(45,60,5), paste(seq(45,60,5),"%",sep=""), mgp=c(2,.5,0))
with(hibbs, text(growth, vote, year, cex=.8))
abline(50, 0, lwd=.5, col="gray")
#+ eval=FALSE, include=FALSE
if (savefigs) dev.off()
#' ### Linear regression
________
Nota: las gráficas no imprimen el acento en las etiquetas
 13.48.53.png)
Entonces estimamos la regresión, y=a+bx+error
M1 <- stan_glm(vote ~ growtn, data=hibbs)
Y luego se imprime:
print(M1)
____
> print(M1)
stan_glm
family: gaussian [identity]
formula: vote ~ growth
observations: 16
predictors: 2
------
Median MAD_SD
(Intercept) 46.3 1.7
growth 3.0 0.7
Auxiliary parameter(s):
Median MAD_SD
sigma 3.9 0.8
___
Imprimir resumen de los antecedentes utilizados
prior_summary(M1)
____
> prior_summary(M1)
Priors for model 'M1'
------
Intercept (after predictors centered)
Specified prior:
~ normal(location = 52, scale = 2.5)
Adjusted prior:
~ normal(location = 52, scale = 14)
Coefficients
Specified prior:
~ normal(location = 0, scale = 2.5)
Adjusted prior:
~ normal(location = 0, scale = 10)
Auxiliary (sigma)
Specified prior:
~ exponential(rate = 1)
Adjusted prior:
~ exponential(rate = 0.18)
------
____
Para mostrar el modelo ajustado, escribimos:
___________
#' **Plot regression line**
#+ eval=FALSE, include=FALSE
if (savefigs) pdf(root("ElectionsEconomy/figs","hibbsline.pdf"), height=4.5, width=5)
#+
par(mar=c(3,3,2,.1), mgp=c(1.7,.5,0), tck=-.01)
plot(c(-.7, 4.5), c(43,63), type="n", xlab="Promedio de crecimiento reciente en los ingresos personales", ylab="Incumbent party's vote share", xaxt="n", yaxt="n", mgp=c(2,.5,0), main="Data and linear fit", bty="l")
plot(c(-.7, 4.5), c(43,63), type="n", xlab="Participación de votos del partido titular", ylab="Participación de votos del partido titular", xaxt="n", yaxt="n", mgp=c(2,.5,0), main="Datos y ajuste lineal", bty="l")
axis(1, 0:4, paste(0:4,"%",sep=""), mgp=c(2,.5,0))
axis(2, seq(45,60,5), paste(seq(45,60,5),"%",sep=""), mgp=c(2,.5,0))
with(hibbs, points(growth, vote, pch=20))
abline(50, 0, lwd=.5, col="gray")
abline(coef(M1), col="gray15")
text(2.7, 53.5, paste("y =", round(coef(M1)[1],1), "+", round(coef(M1)[2],1), "x"), adj=0, col="gray15")
text(2.7, 53.5, paste("y =", fround(coef(M1)[1],1), "+", fround(coef(M1)[2],1), "x"), adj=0, col="gray15")
#+ eval=FALSE,
include=FALSE
if (savefigs) dev.off()
___________
 14.07.04.png)
La primera columna muestra las estimaciones: 46.3 y 3.0 con los coeficientes de la línea ajustada: y=46.3+3.0x. La segunda columna muestra las incertidumbres en las estimaciones utilizando desviaciones absolutas medias. La última línea de salida muestra la estimación y la incertidumbre de 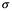 , la escala de la variación en los datos inexplicables por el modelo de regresión (dispersión de los puntos por encima y por debajo de la línea de regresión). Esta figura muestra el modelo lineal que predice la cuota de votos a aproximadamente una precisión de 3.9 puntos porcentuales. El código no es importante explicarlo en este punto del curso, pero es necesario hacernos de los conceptos en este contexto.
, la escala de la variación en los datos inexplicables por el modelo de regresión (dispersión de los puntos por encima y por debajo de la línea de regresión). Esta figura muestra el modelo lineal que predice la cuota de votos a aproximadamente una precisión de 3.9 puntos porcentuales. El código no es importante explicarlo en este punto del curso, pero es necesario hacernos de los conceptos en este contexto.
Algunos de los usos más importantes de la regresión son:
Predicción. Modelado de observaciones existentes o previsión de nuevos datos. Algunos ejemplos con resultados continuos son las participaciones de ventas de productos, elecciones políticas y el estado de salud médico. Ejemplos con resultados discretos o categoría (clasificaciones), incluyen el diagnóstico de enfermedad, la victoria o derrota en un evento deportivo y las decisiones de votación individual.
Explorar asociaciones. Resumen de lo bien que una variable, o conjunto de variables, predicen el resultado. Algunos ejemplos incluyen identificación de factores de riesgo para una enfermedad, las actitudes que predicen el voto y las características que hacen que alguien tenga más probabilidad de tener éxito en un trabajo. De forma más general, se puede utilizar un modelo para explorar asociaciones, estratificaciones o relaciones estructurales entre variables. Algunos ejemplos miden asociaciones entre niveles de contaminación y la incidencia de enfermedades, tasas de detención policial y tasas de crecimiento de diferentes partes de un cuerpo.
Extrapolación. Ajustes de las diferencias conocidas entre las muestras, es decir, los datos observados y una población de interés. Un caso típico es el sondeo: las muestras del mundo real no son completamente representativas, por lo que es necesario realizar algún ajuste para extrapolarlo a la población general. Otro ejemplo es el uso de una muestra auto-seleccionada de escuelas para sacar conclusiones sobre todas las escuelas en un estado. O también, en el uso de datos experimentales de un ensayo de fármacos, junto con las características de fondo de la población completa, para estimar el efecto promedio de la droga en la población.
Inferencia causal. Tal vez el uso más importante de la regresión, es para estimar los efectos del tratamiento. Definimos la inferencia causal con más cuidado más adelante dada la importancia en la formación del estilo de pensamiento científico. Por ahora solo hablamos de comparar los resultados bajo tratamiento de control experimental, o bajo diferentes niveles de tratamiento. En la educación, el resultado podrían ser puntuaciones en una prueba estandarizada, el control podría ser un método particular de aprendizaje y el tratamiento podría ser alguna novela. O en la salud pública, el resultado podría ser la incidencia del asma y el tratamiento continuo podría ser la exposición a algún contaminante. Un desafío clave de la inferencia causal es asegurar que los grupos de tratamiento y control sean similares, en promedio, antes de la exposición al tratamiento, o de lo contrario ajustarse a las diferencias entre estos grupos.
En todos estos ajustes, es crucial que el modelo de regresión tenga suficiente complejidad para llevar la información requerida. Por ejemplo, si la mayoría de los participantes en un ensayo farmacológico son saludables y menores de 60 años, pero hay interés en estimar un efecto promedio entre la población mayor en general, entonces, es necesario incluir la edad y la condición de salud previa como predictores en el mundo de la regresión. Si estos predictores no se incluyen, el modelo simplemente no tendrá suficiente información para permitir el ajuste que queremos hacer.
2.8.1 Algunos ejemplos de regresión
Para dar una idea de la dificultad involucrada en la regresión aplicada, analicemos brevemente algunos ejemplos que implican muestreo, predicción e inferencia causal.
Estimación de la opinión pública a partir de una encuesta de Internet
En un proyecto de investigación Microsoft emplea un modelo de regresión para una muestra conveniente para obtener un monitoreo preciso de la opinión, a una escala de tiempo más nítida y a un costo menor que los métodos tradicionales de encuestas. Los datos provenían de un conjunto de datos de encuestas novedosas y altamente no representativas: una serie de encuestas diarias sobre la intención de votantes en la plataforma de juegos Xbox con un tamaño de muestra total de 750 148 entrevistas de 345 858 encuestados únicos. Este es un problema característico de big data: una muestra muy grande, relativamente económica de recopilar, pero no inmediatamente representativa de la población adulta. Después de ajustar las respuestas de Xbox a través de la regresión multinivel y la posestratificación (MRP), se obtuvieron estimaciones de acuerdo con las previsiones de los principales analistas de encuestas, que se basaron en la agregación de cientos de encuestas tradicionales realizadas durante el ciclo electoral. El propósito no era pronosticar las respuestas individuales de la encuesta, ni identificar predictores importantes o inferencias causales. Más bien, el objetivo era aprender acerca de las tendencias nacionales en la opinión pública y la regresión permitió ajustar las diferencias de muestra y de la población; esto requiere extrapolación[5].
Un experimento aleatorizado desarrollado alrededor de 1970 se realizó a través de un estudio para medir el efecto de un nuevo programa de televisión educativa, la Electric Company, sobre las habilidades de lectura de los niños[6]. Se realizó un experimento en niños de primero hasta cuarto grado de primaria en dos ciudades. Para cada ciudad y grado, los experimentadores seleccionaron de 10 a 20 escuelas, dentro de cada escuela seleccionando las dos clases en el grado cuyos puntajes promedios de las pruebas de lectura eran más bajos. Para cada par, una de estas clases fue asignada aleatoriamente para continuar con su curso de lectura regular y la otra fue asignada para ver el programa de televisión. A cada estudiante se le dio una prueba previa al comienzo del año escolar y una prueba posterior al final. Más allá de las regresiones simples, se requirió un análisis estadístico adicional para ajustar las diferencias en las puntuaciones de las pruebas de pretratamiento entre los dos grupos y para evaluar la incertidumbre en las estimaciones.
Desafíos para construir, comprender e interpretar regresiones. Podemos distinguir dos formas diferentes en las que la regresión se utiliza para la inferencia causal: estimar una relación y ajustar las variables de fondo.
Regresión para estimar una relación de interés
Comience con el escenario más simple de comparabilidad de los grupos de tratamiento y control. Esta condición se puede aproximar por aleatorización, un diseño en el que las personas, o más generalmente, unidades experimentales, se les asignan aleatoriamente los grupos de tratamiento o control, a través de algunos diseños más complicados que aseguran el equilibrio entre los grupos. Por ahora, solo observamos que hay varias maneras de lograr una comparabilidad aproximada de los grupos de tratamiento y control, y de ajustar las diferencias conocidas o modeladas entre los grupos.
Si estamos interesados en el efecto de algún tratamiento x sobre un resultado y, y nuestros datos provienen de un experimento aleatorio o equilibrado, podemos ajustar una regresión, es decir, un modelo que predice y de x, lo que permite la incertidumbre.
Si x es binaria (x=0 para el control o x=1 para el tratamiento) entonces la regresión es particularmente simple; pero la misma idea se mantiene para un predictor continuo. En este entorno, estamos asumiendo la comparabilidad de los grupos asignados a diferentes tratamientos, de modo que un análisis de regresión que prediga el resultado dado el tratamiento nos dé una estimación directa del efecto causal.
 14.02.54.png) .
.  14.03.10.png)
Regresión con tratamiento binario Regresión con tratamiento continuo
 14.03.38.png) .
.  14.03.49.png)
Regresión no lineal Regresión no lineal con tratamiento continuo
Figura 2.10 Ejemplos de análisis de regresión
Pero dejando a un lado esas situaciones, podemos continuar elaborando el modelo de varias maneras para adaptarse a los datos y hacer predicciones más precisas. Una dirección es considerar el modelado no lineal con efecto de tratamiento continuo, dado que muestra lo que sucede si esta curva se ajusta en una línea recta. Otra dirección importante es modelar las interacciones: los efectos del tratamiento que varían en función de otros predictores en el modelo; las interacciones pueden ser importantes. Si nos preocupamos por el efecto del tratamiento, entonces también nos preocupamos por cómo varía este efecto. Tal variación puede ser importante por razones prácticas, por ejemplo, al decidir cómo asignar algún procedimiento médico costoso, o quién está en mayor riesgo de algún peligro ambiental o para el objetivo de la comprensión científica.
Regresión para ajustar las diferencias entre los grupos de tratamiento y control
En la mayoría de los problemas de inferencia causal del mundo real, existen diferencias sistemáticas entre las unidades experimentales que reciben tratamiento y control. En estos ajustes es importante ver las diferencias de pretratamiento entre los grupos de datos y podemos usar la regresión para hacer esto. La clave, es que el efecto estimado se base necesariamente en modelos, pero el punto es que cuando hay desequilibrios entre los controles tratados y los controles en un predicador importante, se debe realizar algún ajuste.
Interpretación de coeficientes en un modelo predictivo
Puede haber desafíos en la interpretación de modelos de regresión, incluso en el caso más simple de predicción pura. La regresión es, sin embargo, algo útil para explorar una asociación, ya que muestra que la pendiente estimada es positiva (con un error estándar asociado que transmite incertidumbre en esa pendiente). Como inferencia de muestreo, los coeficientes de regresión pueden interpretarse directamente en la medida en que las personas de la encuesta son una muestra representativa de la población de interés; de lo contrario, es mejor incluir predictores adicionales en el modelo para cerrar la brecha de la muestra a la población. Interpretar la regresión como una inferencia causal puede sentirse natural. Pero tal interpretación es cuestionable porque las personas pueden diferir de muchas maneras, por ejemplo la estatura no es un tratamiento asignado aleatoriamente. Observar un patrón en los datos podría incitar a un investigador por ejemplo a realizar más experimentación para estudiar las razones por las que las personas más altas pudieran percibir mayor ingreso laboral que las personas más bajitas.
La idea de un modelo de regresión es construir una fórmula simple para predecir un resultado. Se trata de un sistema “lineal”, pero tenga en cuenta que se han incluido interacciones que son esencialmente más complejas, características combinadas. Muchos enfoques de regresión más sofisticados están disponibles para hacer frente a problemas grandes y complejos, como modelos no lineales y un proceso llamado LASSO, que simultáneamente estima coeficientes y selecciona variables predictor relevantes, esencialmente estimando sus coeficientes como cero[7].
Los árboles de clasificación y los modelos de regresión surgen de la filosofía de modelado algo diferentes. Los árboles intentan construir reglas simples que identifican grupos de casos con resultados esperados similares, mientras que los modelos de regresión se centran en el peso que se debe dar a características específicas, independientemente de qué más se observe en un caso. Todo esto apunta a que la posibilidad cuantitativa puede no ser el único criterio para un algoritmo, y una vez que el rendimiento es suficientemente bueno, puede ser razonable intercambiar pequeños cambios para conservar la necesidad de simplicidad.
¿Qué tan seguros podemos estar de lo que está pasando en estimaciones e intervalos?
Reconocer la incertidumbre es importante. Cualquiera puede hacer una estimación, pero ser capaz de evaluar de manera realista su posible error es un elemento circular de la ciencia estadística. A pesar de que implica algunos conceptos desafiantes.
Supongamos que hemos recuperado unos datos precisos, tal vez con una encuesta bien diseñada, y queremos generalizar los resultados a nuestra población de estudio. Si hemos sido cuidadosos y evitamos sesgos internos, entonces, debemos esperar que las estadísticas resumidas calculadas a partir de la muestra estén cerca de los valores correspondientes para la población del estudio.
Es importante este punto, porque vale la pena explorar más a fondo. En un estudio bien realizado, esperamos que nuestra medida de muestra esté cerca de la media de la población, que del rango intercuartil de la población… En la escritura estadística más fina y técnica, estas dos figuras se distinguen generalmente por darles letras romanas y griegas respectivamente, en un intento de evitar confusión, por ejemplo; m a menudo representa la media de la muestra, 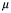 es la media de la población, s generalmente representa una desviación estándar de la muestra y
es la media de la población, s generalmente representa una desviación estándar de la muestra y 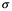 (sigma) una desviación estándar de la población. Estos detalles son importantes si no solo queremos dar una visión amplia de lo que está pasando en el contexto, el tamaño de muestra grande y confiable es una señal necesaria de confiabilidad en muchos casos.
(sigma) una desviación estándar de la población. Estos detalles son importantes si no solo queremos dar una visión amplia de lo que está pasando en el contexto, el tamaño de muestra grande y confiable es una señal necesaria de confiabilidad en muchos casos.
Ahora llegamos a un paso crítico. Con el fin de averiguar cuán precisas podrían ser estas estadísticas, tenemos que pensar en cuánto podrían cambiar nuestras estadísticas en nuestra imaginación sí repitiéramos el proceso de muestreo muchas veces. En otras palabras, si extrajimos repetidamente muestras ¿Cuánto variarían las estadísticas calculadas? Si supiéramos cuánto variarían estas estimaciones, entonces nos ayudaría a decirnos cuán precisa era nuestra estimación real. Pero, lamentablemente, solo podríamos encontrar la variabilidad precisa en nuestras estimaciones si conociéramos con precisión los detalles de la población. Y esto es exactamente lo que no sabemos.
Hay dos maneras de resolver esta circularidad. La primera es hacer algunas suposiciones matemáticas sobre la forma de distribución de la población, y utilizar sofisticadas teorías de probabilidad para averiguar qué esperaríamos en nuestra estimación y por lo tanto, cuán lejos podríamos esperar, digamos, que el promedio de nuestra muestra sea la media de la población. Este es el método tradicional que se enseña en los libros clásicos de estadística.
Sin embargo, existe un enfoque alternativo, basado en la suposición plausible de que la población debe parecerse más o menos a la muestra. Dado que no podemos extraer repetidamente una nueva muestra de la población, en su lugar, extraemos repetidamente nuevas muestras de nuestra muestra.
Por lo tanto, tenemos una idea de cómo nuestra estimación varía a través de este proceso de remuestreo con reemplazo. Esto se conoce como arrancar los datos: la idea refleja la capacidad de aprender acerca de la variabilidad en una estimación sin tener que hacer ninguna suposición sobre la forma de la distribución de la población. Esto se conoce como distribución de muestreo de estimaciones, ya que refleja la variabilidad en las estimaciones que surgen del muestreo repetido de datos.
Qué nos muestra claramente esta característica. Primero, quizás lo más notable, es que casi todo el rastro de la asimetría de las muestras originales ha desaparecido: las distribuciones alrededor de la media de los datos originales son cuasi simétricas. Este es el primer atisbo de lo que se conoce como el Teorema del Límite Central, que dice que la distribución de los promedios de las muestras tienden hacia la forma de una distribución normal con un tamaño de muestra creciente, casi independiente de la forma de la distribución de datos originales. Este es un resultado excepcional. Fundamentalmente, estas distribuciones de arranque nos permiten cuantificar nuestra incertidumbre sobre las estimaciones mostradas.
En resumen, la variabilidad de las estadísticas basadas en muestras; es decir, datos de arranque cuando no queremos hacer suposiciones sobre la forma de distribución de la población; el hecho de que la forma de la distribución de las estadísticas no depende de la forma de la distribución original de la que dibujamos puntos de datos individuales, es un asunto clave a considerar.
Esta estrategia de arranque se puede aplicar a situaciones más complejas. La hemos adaptado dentro de la discusión de la regresión a los datos, lo que permite hacer predicciones, digamos, utilizando regresiones con un gradiente estimado. ¿Qué tan seguros podemos estar de la posición de esta línea ajustada? Es una manera intuitiva e intensiva de evaluar la incertidumbre en nuestras estimaciones, sin hacer suposiciones fuertes y sin usar la teoría de probabilidad. Pero la técnica no es factible cuando se trata, digamos, de elaborar los márgenes de error en, por ejemplo, encuestas de desempleo a 100,000 personas. Aunque el arranque es una idea simple, brillante y extraordinariamente efectiva, es demasiado torpe para arrancar en grandes cantidades de datos, especialmente cuando existe una teoría conveniente que puede generar fórmulas para el ancho de los intervalos de incertidumbre (aunque primero debemos enfrentar la desafiante teoría de la probabilidad).
2.9 Creación, interpretación y comprobación de modelos de regresión
El análisis estadístico pasa por tres pasos:
- Creación de modelos, comenzando con modelos lineales de la forma y=a + bx + error y expandiéndose a través de predictores, interacciones y transformaciones adicionales.
- Los ajustes al modelo, que incluyen manipulación de datos, programación y uso de algoritmos para estimar los coeficientes de regresión y sus incertidumbres y para hacer predicciones probabilísticas.
- Comprender los ajustes al modelo, lo que implica gráficos, más programación y una investigación activa de las conexiones entre mediciones, parámetros y los objetos de estudio subyacentes.
Un desafío en el trabajo aplicado serio, es cómo ser críticos sin ser nihilistas, aceptar que podemos aprender del análisis estadístico: podemos generalizar de la muestra a la población, del tratamiento al control y de las mediciones observadas a la construcción subyacente de interés, incluso mientras estas inferencias pueden ser erróneas. Un paso clave es seguir los pasos que vinculan las afirmaciones más grandes con los datos y el análisis estadístico.
2.10 Inferencia clásica y bayesiana
Los estadísticos gustan, considerar que gran parte de su esfuerzo, es ajustar modelos a datos y utilizar esos modelos para hacer predicciones. Estos pasos se pueden realizar bajo diversos marcos metodológicos y filosóficos. Comunes a todos estos enfoques son tres preocupaciones: 1) qué información se está utilizando en el proceso de estimación, 2) qué suposiciones se están haciendo desde los fundamentos y 3) cómo se interpretan las estimaciones y predicciones, en un marco clásico o bayesiano.
Información
El punto de partida para cualquier problema de regresión son los datos de una variable de resultado “y” y uno o más predictores “x”. Cuando los datos son continuos y hay un único predictor, los datos se pueden mostrar como una gráfica de dispersión. Cuando hay un predictor continuo o predictor binario, los datos se pueden mostrar como una gráfica de dispersión con dos símbolos diferentes, tratamiento y control. En términos más generales, no siempre es posible presentar todos los datos en una sola pantalla.
 14.30.12.png)
Además de los datos en sí, normalmente sabemos algo sobre cómo se recopilaron. Por ejemplo en una encuesta, por medio de sensores electrónicos. Si los datos son ensayos de laboratorio, podríamos tener conocimiento de los sesgos y la variación de las mediciones y así sucesivamente.
También debe haber información disponible sobre los datos que se observaron en absoluto. En una encuesta de una población bien definida o podríamos ser una muestra de conveniencia, en cuyo caso deberíamos tener alguna idea de qué tipo de personas eran más o menos propensas a ser afectadas por tal efecto. En un experimento los tratamientos pueden asignarse al azar o no, en cuyo caso normalmente tendremos alguna información sobre cómo se realizó la asignación. Por último, normalmente tenemos conocimientos previos provenientes de fuentes distintas de los datos en cuestión, basados en la experiencia con estudios anteriores similares. Tenemos que tener cuidado en cómo incluir dicha información.
Suposiciones
Hay tres tipos de suposiciones que son esenciales para cualquier modelo de regresión de un resultado “y” y dados los predictores “x”. Primero es la forma fundamental de la relación entre x y y: normalmente asumimos la linealidad, pero esto es más flexible de lo que podría parecer, ya que podemos realizar transformaciones de predictores o resultados, y también podemos combinar predictores de manera lineal o no lineal. Aún así, las opciones de transformación, así como la elección de qué variables incluir en el modelo en primer lugar, corresponden a suposiciones sobre las relaciones entre las diferentes variables que se están estudiando.
El segundo conjunto de suposiciones implica de dónde provienen los datos: qué observaciones potenciales se ven y cuáles no, quién es encuestado y quién no responde, quién recibe qué tratamiento experimental, etc. Estas suposiciones pueden ser simples y fuertes, asumiendo el muestreo aleatorio o la asignación aleatoria de tratamiento, o más débiles, por ejemplo, permitiendo que la probabilidad de respuesta en una encuesta sea diferente para hombres y mujeres y que varíe según la etnia y la educación, o permitiendo que la probabilidad de asignación de un tratamiento médico varíe según la edad y el estado de salud anterior. Las suposiciones más fuertes, como la asignación aleatoria, tienden a ser simples y fáciles de atender, siendo más generales, también pueden ser más complicadas.
El tercer conjunto de suposiciones requeridas en cualquier modelo estadístico implica la relevancia real de los datos medidos: ¿son precisas las respuestas de las encuestas, pueden generalizar el comportamiento en un experimento de laboratorio al mundo exterior, las mediciones de hoy son predictivas de lo que podría suceder mañana? Estas preguntas se pueden estudiar estadísticamente comparando la estabilidad de las observaciones realizadas de diferente manera o en diferente momento, pero en el contexto de la regresión se dan típicamente por sentado. La interpretación de una regresión de y en x depende también de la relación entre la x medida y los predictores subyacentes de interés, y de la relación entre la y medida y los resultados subyacentes de interés.
Inferencia clásica
El enfoque tradicional del análisis estadístico se basa en resumir la información en los datos, no utilizando información previa, sino obteniendo estimaciones y predicciones que tienen propiedades estadísticas bien entendidas, bajo sesgo y bajo varianza. Esta actitud a veces se llama “frecuentacionista”, ya que el estadístico clásico está interesado en las expectativas a largo plazo de sus métodos, es decir, las estimaciones deben ser correctas en promedio (imparcialidad), los intervalos de confianza deben cubrir el verdadero valor del parámetro 95% del tiempo (cobertura). Un principio importante de la estadística clásica es el conservadurismo: a veces los datos son débiles y no podemos hacer declaraciones fuertes, pero nos gustaría poder decir, al menos aproximadamente, que nuestras estimaciones son imparciales y nuestros intervalos tienen la cobertura anunciada. En las estadísticas clásicas debe haber una ruta clara e inequívoca (“objetiva”) de los datos a las inferencias, que a su vez debe ser comprobable, al menos en teoría, en función de sus propiedades de frecuencia.
Las estadísticas clásicas tienen mucho que ofrecer, y hay una apelación para solo resumir la información de los datos. Las debilidades del enfoque clásico surgen cuando los estudios son pequeños y los datos son indirectos o altamente variables.
Inferencia bayesiana
Es un enfoque de las estadísticas que incorpora información previa en las inferencias, yendo más allá del objetivo de simplemente resumir los datos existentes. Se puede utilizar la información como una distribución previa donde el efecto multiplicativo del tratamiento es probable que esté en un rango específico. Combinando esto con los datos y utilizando las reglas de la inferencia bayesiana, obtenemos un intervalo posterior, digamos 95%, que oscila entre un efecto negativo del 8% de la intervención hasta un posible efecto positivo digamos de un 28%. Basándonos en este análisis bayesiano, nuestra mejor conjetura de la diferencia observada en un estudio de realización futuro es mucho menor que el 42%.
Este sencillo ejercicio mental ilustra tanto la fuerza como las debilidades de la inferencia bayesiana. En el lado positivo, el análisis da resultados más razonables y se puede utilizar para hacer predicciones directas sobre resultados futuros y sobre los resultados de experimentos futuros. En el lado negativo, se requiere una información adicional: la distribución previa, que en este caso representa la información tal vez polémica de que el efecto del tratamiento sobre las ganancias es probablemente inferior al 10%. Para bien o para mal, no podemos tener uno sin el otro: en la inferencia bayesiana, la distribución previa representa la arena sobre la cual se evaluarán las predicciones. En un mundo en el que el tratamiento podría duplicar plausiblemente las ganancias medias, la estimación bruta, digamos de 1.42 y un intervalo de [1.02,1.98] producen predicciones razonables. Pero un contexto en el que tales efectos enormes se presenten es inverosímil, debemos ajustar nuestras expectativas y predicciones en consecuencia.
Por lo tanto, en ese sentido, tenemos una opción: la inferencia clásica, que conduce a resúmenes puros de datos que pueden tener un valor limitado como predicciones; o inferencia bayesiana, que en teoría puede producir predicciones válidas incluso con datos débiles, pero se basa en suposiciones adicionales. Aquí no hay una respuesta universalmente correcta; debemos ser conscientes de nuestras opciones.
También hay una ventaja práctica del enfoque bayesiano, donde todas sus inferencias son probabilísticas y por tanto pueden ser representadas por simulaciones aleatorias. Por esta razón, siempre que queramos resumir la incertidumbre en la estimación más allá de los simples intervalos de confianza, y siempre que queremos usar modelos de regresión para las predicciones, tomaremos el enfoque bayesiano.
Referencias
[1] Zhou, Hong. (2020). Linear Discriminant Analysis. 10.1007/978-1-4842-5982-5_4.
[2] McCullagh, Peter. (1992). Introduction to Nelder and Wedderburn (1972) Generalized Linear Models. 10.1007/978-1-4612-4380-9_38.
[3] Gehrke, Johannes. (2008). Classification and Regression Trees. 10.4018/9781605660103.ch031.
[4] Wood, Simon. (2020). Inference and computation with generalized additive models and their extensions. TEST. 10.1007/s11749-020-00711-5.
[5] Ben Salem, Mayssa. (2020). PUBLIC OPINION RESEARCH. 8. 31-36.
[6] Woody, Robert. (1974). Educational television programming and school health. The Journal of school health. 44. 246-9. 10.1111/j.1746-1561.1974.tb04443.x.
[7] Klosa, Jan & Simon, Noah & Westermark, Pål & Liebscher, Volkmar & Wittenburg, Dörte. (2020). Seagull: lasso, group lasso and sparse-group lasso regularization for linear regression models via proximal gradient descent. BMC bioinformatics. 21. 407. 10.1186/s12859-020-03725-w.
Autores:
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Berenice Yahuaca Juárez
Erasmo Cadenas Calderón
Abraham Zamudio Durán
Lizbeth Guadalupe Villalon Magallan
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán
Monica Rico Reyes