Texto universitario

_____________________________

Módulo 1. La estadística  

1.1 Modelos

Para esbozar el argumento del pensamiento aplicando muchos modelos a la vez, comenzaremos con una cita de T.S. Eliot: ¿Dónde está la sabiduría que hemos perdido en el conocimiento? ¿Dónde estará el conocimiento que hemos perdido en la información? A eso podríamos añadir, ¿dónde está la información que hemos perdido en todos los datos? 

Eliot cuestiona, y con ello advierte que la realidad se puede formalizar en jerarquías que se encuentran en los datos de eventos, experiencias y fenómenos sin procesar y sin codificar. Los datos pueden ser cadenas largas de ceros y unos, marcas de tiempo, vínculos entre páginas…, los datos por sí solos carecen de significado, organización y estructura. Es necesario nombrar la información en categorías y particiones de datos. Así vivimos en una era de abundante información. Hace un siglo y medio, conocer la información trajo estatus económico y social. Hoy no importa, no la podemos abarcar ni siquiera de un solo tema, lo que importa es poner en uso su procesamiento intelectual para predicar, explicar, controlar… Por lo menos la mitad de la batalla es conocimiento de cómo poner la información en uso.

Platón definió el conocimiento como una verdadera creencia justificada. Una definición moderna refieren al conocimiento como comprensión de las relaciones correlativas, causales y lógicas. El conocimiento organiza la información. El conocimiento a menudo toma la forma de modelo: económico, metabólico, fotosintético, físico, químico, literario, epistémico, ontológico, psicológico… Esos modelos explican (disertación, teoría) y predicen (estructuras matemáticas). En lo alto de la jerarquía se encuentra la sabiduría, la capacidad de identificar y aplicar el conocimiento relevante. La sabiduría requiere pensamiento apoyado en muchos modelos. A veces, la sabiduría consiste en seleccionar el mejor modelo, cómo dibujar una línea a partir de un caos de direcciones. Otras veces se puede promediar entre modelos al tomar medias, las personas sabias aplican pruebas diagnósticas para descartar o explorar soluciones. 

El valor de los modelos también reside en su capacidad para revelar las condiciones bajo las cuales se mantienen los resultados. Los modelos revelan condiciones similares para nuestras intuiciones. Con los modelos podemos analizar cuánto se propagan las enfermedades en un cierto tiempo, cuándo hay un equilibrio en los mercados, y cuándo las sociedades reclaman cambios políticos.

Al construir un modelo, este debe apegarse a un enfoque de realización, analogía o modelos bayesianos sin limitar su alcance para materializar su desarrollo y alcance. Podemos aspirar al realismo y seguir un enfoque de realización. Estos modelos incluyen las piezas importantes y revelan dimensiones y atributos innecesarios o los agrupan. Los modelos ecológicos, legales, de sistema de tráfico toman este enfoque, por ejemplo los modelos climáticos y del cerebro son de este tipo. También, en su  lugar podemos tomar un enfoque por analogía y abstracto de la realidad. Podemos modelar la propagación del crimen como una enfermedad y tomar posiciones políticas en un sentido de derecha o izquierda. 

Mientras el enfoque de realización enfatiza el realismo, el enfoque de analogía intenta la esencia de un proceso, sistema o fenómeno. Cuando un físico asume fricción, pero hace suposiciones realistas, toma el enfoque de realización. Cuando un economista representa a las empresas competidoras como diferentes especies y define nichos de productos, hace analogías. Lo hacen usando un modelo desarrollado para encarnar un sistema diferente. Modelos psicológicos del aprendizaje asignan pesos a alternativas, agrupan las respuestas de dopamina y otros factores, también invocan la analogía de una escala en la que equilibramos las alternativas.

El tercer enfoque, los modelos bayesianos, no representa la captura la realidad. Estos modelos funcionan como parques analíticos y computacionales en los que podemos explorar posibilidades. Este enfoque permite descubrir ideas generales que se aplican fuera de nuestro mundo físico y social en espacios sintéticos. Nos ayuda a entender las implicaciones de las limitaciones del mundo real. Aunque no son realistas, el modelo produce información sobre la auto-organización, la complejidad y algunos argumentos, incluso sobre la vida misma. 

Ya sea que se incluyan en una realidad más compleja, creando una analogía o construyendo un mundo inventado para explorar ideas, un modelo debe ser capaz de escribirse en un lenguaje formal transmisible y manejable, generalmente expresado en el lenguaje matemático o informático. Al escribir un modelo, no podemos eliminar los términos como creencias o preferencias sin proporcionar una descripción formal. Las creencias se pueden representar como una distribución de probabilidad sobre un conjunto de eventos o antecedentes. Las preferencias se pueden representar de varias maneras, como una clasificación sobre un conjunto de alternativas o como una función matemática. 

Cuán manejable es algo, significa lo susceptible de su análisis. En el pasado, el análisis se basaba en el razonamiento matemático o lógico. Un modelador tenia que ser capaz de probar cada paso en un argumento. Esta restricción condujo a una estética que valoraba los modelos hipotéticos deductivos. El fraile inglés y teólogo Guillermo de Ockham (1287-1347) escribió: la pluralidad nunca debe ser postulada sin necesidad. Einstein asumió este principio: todo debe ser lo más simple posible, pero no más simple. Hoy en día cuando nos enfrentamos a la restricción de la capacidad analítica, podemos recurrir al cálculo. Podemos construir modelos elaborados con muchas piezas móviles (variables) sin preocuparnos por la capacidad analítica. Los científicos toman este enfoque para construir un modelo sobre el clima global, el cerebro, os incendios forestales, la propagación de virus. Aún en este enfoque se reconoce que podría requerir una gran cantidad de partes móviles. 

El uso de modelos:

Aportar razones: identificar condiciones y deducir implicaciones lógicas.

Explicar: proporcionar explicaciones (comprobables) de fenómenos empíricos.

Diseño: elegir características de un producto, una política institucional o reglas de operación.

Comunicar: relacionar conocimiento y entendimiento.

Toma de decisiones: orientar la toma de decisiones y acciones estratégicas.

Predicción: hacer predicciones numéricas y categorías de fenómenos futuros y desconocidos.

Explorar: investigación de posibilidades de conocimiento e hipótesis.

Razones

Al construir un modelo, identificamos los conceptos operativos (actores o variables) y entidades más importantes junto con características relevantes. A continuación, escribimos cómo esas partes interactúan y agregan efectos significativos, lo que nos permite derivar lo que sigue de qué y por qué. Al hacerlo, mejoramos nuestro razonamiento. Aunque lo que podemos derivar depende de lo que podemos asumir como causal, descubrimos más que tautologías. Rara vez podemos inferir toda la gama de implicaciones de nuestras suposiciones en inspecciones unilaterales de sí mismas. Necesitamos lógica formal. La lógica también revela posibilidades e imposibilidades. Con ella, podemos derivar relaciones precisas y a veces inesperadas estructuras de la realidad. Podemos descubrir la condicionalidad de nuestras intuiciones. 

El teorema de Arrow proporciona un ejemplo de cómo la lógica revela las imposibilidades. El modelo aborda la cuestión de si las preferencias individuales se agregan para formar una referencia colectiva. Este modelo representa las preferencias individuales como clasificaciones ordinarias sobre alternativas. Dentro de los modelos, hacemos suposiciones y probamos teoremas. Dos teoremas que están de acuerdo en la acción óptima, pueden hacer predicciones diferentes u ofrecer explicaciones distintas, pero necesariamente, deben hacer suposiciones diferentes. 

Explicar

Los modelos proporcionan explicaciones lógicas claras para los fenómenos empíricos. Los modelos en física explican la velocidad de los objetos que caen y la forma de las trayectorias. Los modelos biológicos explican las distribuciones de las especies. Los modelos epidemiológicos explican la velocidad y el patrón de propagación de la enfermedad. Los modelos geofísicos explican la distribución de los terremotos. 

Los modelos pueden explicar los valores de puntos y los cambios en sus valores. Los modelos también explican la forma de las funciones de respuestas significativa. Los modelos más eficaces explican tanto los resultados sencillos como los desconcertantes. Una explicación  incluye suposiciones formales y cadenas causales explícitas. Esas suposiciones y cadenas causales pueden ser por ejemplo, los altos niveles de comportamiento criminal, como la percepción de una baja probabilidad de ser capturado.  

Distribuciones

Las distribuciones forman parte de la base de conocimiento principal para cualquier modelador. También requerimos un conocimiento práctico de las distribuciones para medir la desigualdad educativa, los ingresos o riqueza para realizar pruebas estadísticas. Como modeladores nos interesan las grandes preguntas. ¿Por qué estudiar las distribuciones y por qué importan?

Para abordar la primer gran pregunta, tenemos que volver a familiarizarnos con lo qué son distribuciones. Una distribución captura matemáticamente la variación (diferencias dentro de un tipo) representándolas como distribuciones de probabilidad definidas sobre valores numéricos o categorías. Una distribución normal toma forma de curva de campana de Gauss. Las alturas y pesos de la mayoría de las especies satisfacen las distribuciones normales. Son simétricas alrededor de su media y no incluyen eventos particularmente grandes o pequeños. Podemos confiar en el teorema de límite central para explicar la prevalencia de distribución normal. Nos dice que cuando sumamos o promediamos variables aleatorias, podemos esperar obtener una distribución normal. Muchos fenómenos empíricos, en particular cualquier agregado como datos de alturas o totales de votos, se pueden escribir como sumas de eventos aleatorios. No todos los tamaños de eventos son normales. Los terremotos, las muertes por la guerra y las ventas de libros exhiben distribuciones de cola larga: consisten principalmente en eventos diminutos, pero incluyen a los ocasionales. 

Saber si un sistema produce una distribución normal o de cola larga importa por cualquier número de razones. Queremos saber si una red eléctrica sufrirá interrupciones masivas, o si un sistema de mercado producirá un puñado de multimillonarios y miles de personas pobres. Con el conocimiento de las distribuciones, podemos predecir la probabilidad de que las aguas de inundaciones excedan las paredes de un dique; la probabilidad de que un vuelo llegue a tiempo y las probabilidades de que un fraccionamiento cueste el doble de su cantidad presupuestada. El conocimiento de las distribuciones también es relevante en el diseño. Las distribuciones no implican grandes desviaciones, por lo que los diseñadores pueden trabajar sobre márgenes pequeños. Una comprensión de las distribuciones puede guiar las acciones. 

Una distribución asigna probabilidades a eventos o valores. La distribución asigna valores posibles de los resultados. Las medias estadísticas condensan la información contenida en una distribución en números únicos, como la media, el valor medio de la distribución. Por ejemplo, la altura media de un árbol de pino mexicano podría ser de 15 metros, y el tiempo medio que le toma crecer podría ser 25 años. Los científicos sociales confían en las medias para comparar las condiciones económicas y sociales entre los países. Una segunda estadística, la varianza, mide la dispersión de una distribución: el promedio de la distancia cuadrada de los datos a la media. Si cada punto de una distribución tiene el mismo valor, la varianza es igual a cero. Si la mitad de los datos tiene valor 4 y la mitad tiene el valor 10, entonces, en promedio, cada punto se encuentra a una distancia de 3 de la media y la varianza es igual a 9. La desviación estándar de una distribución, otra estadística común, es igual a la raíz cuadrada de la varianza. 

El conjunto de distribuciones es ilimitado. Podríamos dibujar cualquier línea en un pedazo de papel gráfico e interpretarlo como una distribución de probabilidad. Afortunadamente, las distribuciones que encontramos tienden a pertenecer a unas pocas clases. La distribución más común, la distribución normal, o curva de campana es presentada a continuación.

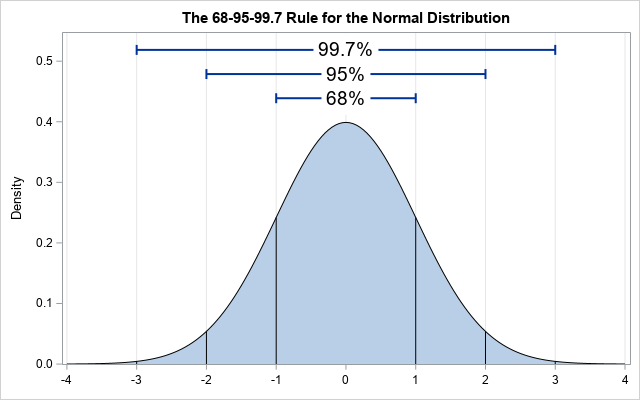
Figura 1.1 distribución normal

Las distribuciones normales son simétricas sobre su media. Si la media es igual a cero, la probabilidad de un empate mayor que 3 es igual a probabilidad de un empate menor que -3. Una distribución normal se caracteriza por su media y desviación estándar (o, equivalentemente, su varianza). En otras palabras, los gráficos de la distribución normal parecen idénticos en simetría, con aproximadamente el 68% de todos los resultados dentro de una desviación estándar de la media, el 95% de todos los resultados dentro de dos desviaciones estándar, y más del 99% dentro de tres desviaciones estándar. Las distribuciones normales permiten cualquier resultado o evento de tamaño, aunque los eventos grandes son raros. Un evento dentro de cinco desviaciones estándar de la media ocurre aproximadamente una vez cada 2 millones de sorteos. 

La lógica del teorema de límite central. Ningún fin de los fenómenos exhibe una distribución normal: tamaños físicos de la flora, fauna, calificaciones de exámenes, ventas diarias en tiendas de conveniencia y la vida útil de los erizos de mar. El teorema del límite central, indica que agregar o promediar variables aleatorias produce una distribución normal, y podemos brindarle una explicación:

La suma de N mayor o igual que 20 variables aleatorias será aproximadamente una distribución normal siempre que las variables aleatorias sean independientes, que cada una tenga una varianza finita y que ningún conjunto pequeño de las variables contribuya la mayor parte de la variación. Cualquiera de las varias condiciones son suficientes. Una de las más comunes, la condición de Lindeberg, requiere que la proporción de la variación total que proviene de cualquier variable converjará a cero a medida que el número de variables crece. 

Un aspecto de este teorema es que las variables aleatorias en sí no necesitan ser distribuidas normalmente. Podrían tener cualquier distribución siempre y cuando cada una tenga varianza finita y ningún pequeño subconjunto de ellos aporte la mayor parte de la varianza. 

Podemos aplicar el teorema de límite central para explicar la distribución de estaturas humanas. La altura de una persona está determinada por una combinación genética, el entorno y la interacción entre ambas condicionantes. La contribución genética podría ser tan alta como 80%, por lo que asumiremos que la altura depende solo de los genes^[1]. Al menos 180 genes contribuyen a la altura humana^[2]. Un gen puede contribuir a tener un cuello más largo y otro una tibia más larga. Aunque los genes interactúan, hasta una primera aproximación, podemos suponer que cada uno contribuye de forma independiente. Si la altura es igual a la suma de las contribuciones de los 180 genes, entonces las alturas se distribuirán normalmente. Por la misma lógica, también lo harán los pesos de los gatos y la longitud de los pulgares de un oso. 

Tengamos presente que una distribución normal, el 95% de los resultados se encuentra dentro de dos desviaciones estándar y el 99% se encuentra dentro de tres desviaciones estándar y por el teorema del límite central, la media de una colección de variables aleatorias independientes se distribuirá normalmente (con la advertencia de la varianza). De ello se deduce que podemos estar bastante seguros de que los promedios de la población en las puntuaciones de las pruebas y similares se distribuirán normalmente. La desviación estándar del promedio de las variables aleatorias, sin embargo, no es igual a la media de las desviaciones estándar de las variables, ni la desviación estándar de la suma es igual a las suma de las desviaciones estándar. En su lugar, esas fórmulas dependen de las raíces cuadradas de los tamaños de población. 

Las desviaciones estándar de la media σ_μ y de la suma y la suma de N variables aleatorias independientes cada una con de desviación estándar son dadas por

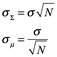
La fórmula para la desviación estándar de la media implica que las poblaciones grandes tienen desviaciones estándar mucho más bajas que las pequeñas. A partir de esto, podemos inferir que deberíamos ver más cosas buenas y más cosas malas en poblaciones pequeñas. Y de hecho lo hacemos. Los lugares más seguros para vivir son los pueblos pequeños , estos hechos pueden explicarse por las diferencias en las desviaciones estándar. Si no se tiene el tamaño de la muestra y se deduce la causalidad de los valores atípicos, se pueden realizar acciones de decisión incorrectas. Por esta razón, Howard Wainer se refiere a la fórmula para la desviación estándar de la media la “ecuación más peligrosa del mundo^[3]”. También utilizamos la regularidad de la distribución normal para probar las diferencias significativas en los valores medios. Si una media empírica muestra más de dos desviaciones estándar de una media hipotética, los científicos sociales rechazan la hipótesis de que las medias son las mismas. 

Los físicos, sin embargo, podrían no rechazar la hipótesis, al menos no si los datos provienen de un experimento de física. Los físicos imponen estándares más estrictos porque tienen conjuntos de datos más grandes; hay muchos más átomos que personas y datos más limpios. Los físicos de evidencia en los que se basó la existencia del bosón de Higgs en 2012, ocurrirían aleatoriamente su aparición al menos una vez en 7 millones de ensayos si el bosón de Higgs no existiera. 

1.1.1 Convertir a la realidad en datos

El enfoque estadístico supone reducir los hechos a números que puedan ser contados y dibujados en gráficos. Esto en principio podría parecer frío y deshumanizador, pero si vamos a usar la ciencia estadística para iluminar la realidad, entonces nuestras experiencias diarias tienen que convertirse en datos, y esto significa categorizar y etiquetar eventos, registrar mediciones, analizar los resultados y comunicar las conclusiones. Sin embargo, la simple categorización y el etiquetado pueden suponer un serio desafío. Tome la siguiente pregunta básica, que debería ser de interés para todos los preocupados por el estado de nuestro medio ambiente: ¿Cuántos árboles hay en nuestro planeta? Antes incluso de empezar a pensar en cómo responder a esta pregunta, primero tenemos que resolver una cuestión bastante básica. ¿Qué es un árbol? Es posible que sienta que conoce un árbol cuando lo ve, pero su juicio puede diferir considerablemente de los otros que podrían considerarlo un arbusto robusto. Así que para convertir la experiencia en datos, tenemos que empezar con definiciones rigurosas.

En este sentido, los investigadores por lo general toman una serie de áreas con un tipo común de paisaje, conocido como bioma y cuentan el número promedio de árboles encontrados por kilómetro cuadrado. Luego utilizando grafos de satélite estiman el área total del planeta cubierta por cada tipo de bioma, estos modelos estadísticos finalmente estimaron 3.04 billones de árboles en el planeta. Esto suena mucho pero en realidad esperaban encontrar el doble de este número^[4]. 

Los datos tienen dos limitaciones principales como fuente de tales conocimientos. En primer lugar, casi siempre es una medida imperfecta de lo que realmente nos interesa. En segundo lugar, cualquier cosa que elijamos medir diferirá de un lugar a otro, de persona a persona, y de vez en cuando, el problema es extraer ideas significativas de toda esta variabilidad aparentemente aleatoria. Durante años la ciencia estadística ha enfrentado estos desafíos, ha proporcionado la base para interpretar los datos, que siempre es imperfecta, con el fin de distinguir las relaciones importantes de la variabilidad de fondo que nos hace a todos únicos. Pero el mundo siempre está cambiando, a medida que nos hacemos nuevas preguntas, disponemos de nuevas fuentes de datos, la ciencia estadística, también ha tenido que cambiar.

Las personas siempre han medido y contado, pero las estadísticas modernas realmente nacieron como disciplina alrededor del año 1650. La probabilidad fue comprendida por Pascal y Pierre de Fermat. Dada esta sólida base matemática para hacer frente a la variabilidad, el progreso fue entonces notablemente rápido, y si además, está apoyado en la informática moderna esto potencia más su desarrollo. 

Entonces en el siglo XX, las estadísticas se volvieron más matemáticas, y por desgracia, muchos estudiantes y profesionales, este tema lo convirtieron en herramientas estadísticas, y no como lo que es, argumentación estadística. La idea clásica de herramientas estadísticas se enfrenta a grandes desafíos. En primer lugar, estamos en una era de ciencias de datos, en la que se recopilan grandes conjuntos de datos y complejos monitores en tiempo real, publicaciones en redes sociales y compras en la Internet, estas innovaciones tecnológicas reclaman optimizar algoritmos para el big data. Aunado a ello, la información estadística se ve cada vez más como un componente necesario del perfil del científico, programador, QFB, economista…, así como el conocimiento adecuado del pensamiento argumentativo basado en datos. 

El uso inapropiado de métodos estadísticos estándar ha recibido una parte justa de la culpa por el abuso de métodos estadísticos sobre la ligereza de afirmar que los descubrimientos pueden ser reproducidos por otros investigadores. Lo que se ha conocido como la crisis de reproducibilidad y realización de experimentos en la ciencia^[5]. 

Con la creciente disponibilidad de conjuntos de datos masivos y software de análisis de fácil uso, se podría pensar que hay menos necesidad de capacitar a los estudiantes en métodos estadísticos. Eso sería ingenuo en extremo. Lejos de liberarnos de la necesidad de habilidades estadísticas, datos más amplios y el aumento del número y complejidad de estudios científicos, hace aún más difícil sacar conclusiones apropiadas. Más datos significa que tenemos que ser aún más conscientes de lo que realmente vale la evidencia en la toma de consciencia.

Las rutinas en el procesamiento de los datos, aumentan de hecho, los falsos descubrimientos, tanto debido a un sesgo sistemático inherente a las fuentes de datos como a la realización de muchos análisis en los que solo se informa lo que parece interesante, una práctica a veces conocida como “data-dredging” (degradado de datos^[6]).  Para poder criticar el trabajo científico publicado, o cualquier reporte que encontramos en las noticias de la noche, debemos tener en cuenta una aguda conciencia de los peligros de la presentación selectiva de informes, la necesidad de que las afirmaciones científicas sean replicadas por cuerpos de investigación independientes, y el peligro de una interpretación excesiva de un solo estudio fuera de contexto. Todas estas ideas se pueden reunir bajo el término alfabetización de datos, que describe la capacidad no solo de llevar a cabo análisis estadísticos sobre problemas del mundo real, sino también de comprender y criticar cualquier conclusión extraída por otros sobre la base de la estadística. Pero mejorar la alfabetización argumentativa de la lectura significativa en la educación de las estadísticas, debemos dar más atención a la teoría matemática que a la comprensión de fórmulas y algoritmos, el desafío es hacer de las técnicas un recurso argumentativo para responder a preguntas. Por lo general educar con este enfoque, requiere presentar cada desafío dentro de un problema de interpretación de datos.

Generaciones de estudiantes han sufrido de cursos intensos de una estadística basada en técnicas más que en teoría matemática. La recopilación de los datos requiere el tipo de habilidades organizativas y de codificación que se consideran cada vez más importantes en la ciencia de datos, especialmente porque los datos de fuentes rutinarias pueden necesitar depuración para ser analizados. Una etapa de análisis estadístico cubre recursos técnicos analíticos para visualizar parámetros. Por último la clave de una buena ciencia estadística es extraer conclusiones apropiadas que reconozcan plenamente las limitaciones de la evidencia y la claridad de lo que comunican. Cualquier conclusión plantea más preguntas, así que el ciclo de investigación comienza de nuevo.

1.1.2 Comunicar recuentos y proporciones 

Los datos que registran si los eventos individuales han ocurrido, son denominados datos binarios, ya que solo pueden asumir dos valores, generalmente sí o no. Los conjuntos de datos binarios se pueden resumir por el número de veces y el porcentaje de casos en los que se produjo un evento. 

Una tabla se puede considerar como un tipo de gráfico y requiere cuidadosamente opciones de diseño de color, fuentes y lenguaje para garantizar la comprensión y la legibilidad. Idealmente se deben presentar marcos positivos y negativos para expresar la información imparcial, aunque el orden de interpretación es algo fortuito. 

En esto hay presencia de una variable o concepto operativo. Se define como variable a cualquier medida que pueda tomar diferentes valores en diferentes circunstancias; es dentro de un corto plazo algo muy útil para todo tipo de observación que comprende datos. Las variables binarias son preguntas si/no. Las variables categóricas son medidas que pueden adoptar dos o más categorías:

Categorías no ordenadas; como el país de origen de una persona, el color de su automóvil o el hospital en el que se atendió.

Categorías ordenadas; como el grado de estudios.

Números agrupados; como niveles de temperatura, a menudo se definen en umbrales de intervalos. 

Cuando se trata de presentar datos categóricos, los gráficos de círculo permiten una comprensión del tamaño de cada categoría en relación con el pastel, pero a menudo las áreas distorsionan la independencia de sus conceptos. Múltiples comparaciones es mejor presentarlas son base a las alturas y longitudes de barras horizontales de las proporciones de que se trate. Por lo que sería razonable pensar que comparar proporciones es un asunto trivial. Pero cuando estas proporciones representan estimaciones de los riesgos de experimentar algún daño, entonces se hacen relevantes. Se pueden comunicar los riesgos mediante frecuencias esperadas en lugar de porcentajes o probabilidades. 1 en X es una forma de representar el riesgo, como decir 1 de cada 100 mexicanos terminará el doctorado, esto representa el 1%. Técnicamente, las probabilidades de un evento son la relación entre probabilidad de que el evento suceda contra la posibilidad de que no ocurra. Aunque son extremadamente comunes en la literatura de investigación, las relaciones de probabilidad son una manera  poco intuitiva de resumir las diferencias de riesgo. Si los eventos son raros, entonces las relaciones de probabilidad estarán numéricamente cerca de los riesgos relativos.

Esto pone de relieve el peligro de utilizar las relaciones de probabilidad en cualquier cosa, y la ventaja de informar siempre de riesgos absolutos como cantidad que es relevante para una audiencia, ya sea que se trate de un contagio o cualquier otra cosa de riesgo.

Hemos intentado demostrar cómo tareas aparentemente simples de calcular y comunicar, tales como las proporciones, pueden convertirse en un asunto complejo. De llevarse a cabo con cuidado y conciencia, el impacto de los datos resumidos en parámetros numéricos o gráficos se puede explorar a través de formatos alternativos de presentar la información. La comunicación es una parte importante del ciclo de resolución de problemas y no debemos mostrar preferencias personales. 

Un resumen de datos numéricos puede estar ligado a una ubicación geográfica, tendencia o correlación, está íntimamente relacionado con el cómo los datos se pueden trazar en el papel o en una pantalla. La suave transición entre simplemente reportar parámetros numéricos y tratar de contar una historia a través de una infografía.

La estadística no solo se refiere a eventos graves como el contagio de un virus o el número de cirugías de corazón. En un experimento quizá se desee probar una relación entre consumo de literatura y el declive de la violencia doméstica. Los patrones estadísticos se pueden denominar de manera diversa como distribución de los datos, distribución de muestras o de evidencia empírica. Los diagramas de puntos, simplemente muestran cada punto de datos; la gráfica de barras resume algunas cosas esenciales de la distribución de los datos. Este histograma encuentra cada uno de los intervalos como conjunto de datos, da una idea  aproximada de la forma de distribución.

Estas grafos transmiten inmediatamente algunas características distintivas. La distribución de los datos es muy sesgada, lo que significa que ni siquiera es aproximadamente simétrica alrededor de algún valor central, y tiene un largo  corrimiento por valores muy altos. Pero hay un problema con todos estos gráficos. El patrón de los puntos significa que toda la atención se centra en las conjeturas extremadamente altas, con la mayor parte de los números que se aprietan en el extremo izquierdo. ¿Podemos presentar datos de manera más informativa? Podríamos desechar valores extremadamente altos. Alternativamente podemos transformar los datos de una manera que reduzca el impacto de estos extremos, trazando lo que llamamos una escala logarítmica. 

No hay solo una forma correcta de mostrar conjuntos de números, cada una de las gráficas que hemos citado, tiene alguna ventaja. Los gráficos de tiras muestran puntos individuales, las gráficas de cajas y los histogramas dan una buena sensación de la forma subyacente de la distribución de los datos. 

Las variables que se registran como números vienen en diferentes variedades:

Variables de recuento. Donde las medidas están restringidas a los enteros 0, 1, 2…, Por ejemplo, número de egresados por año, el número de canicas en un frasco.

Variables continuas. Mediciones que se pueden realizar, al menos en principio, con precisión arbitraria. Por ejemplo, altura y peso, cada dato puede variar entre las personas.

Cuando un conjunto de recuentos u observaciones continuas se reducen a una sola estadística de resumen, esto es lo que generalmente llamamos su promedio. Todo esto se familiariza con la idea de interpretar, temperaturas o calificaciones, entre muchos otros contextos.

Hay tres interpretaciones básicas del término promedio, a veces se confunde cuando se refiere como término único al promedio, mediana y moda:

Media: la suma de los números divididos por el número de casos.

Mediana: el valor medio cuando los números se ponen en orden.

Moda: el valor más común.

1.2 Estadística 

La estadística, un poeta diría: es la que nos permite mirar a través de la niebla bizarra del mundo sobre nosotros. Para comprender la realidad subyacente del significado de los datos, la estadística es una tecnología de métodos que nos permiten la extracción del significado dentro de esa niebla. La estadística es esa tecnología para el manejo de la incertidumbre, ese anhelo del hombre de predecir los eventos futuros. Las inferencias acerca de esa neblina, esas que nos arrojan datos de lo desconocido para tomar decisiones, previsiones, análisis de la dinámica de la realidad, son la tarea de las estadísticas. Pero por qué llamarla tecnología y no una disciplina científica. Una tecnología es la aplicación de los conocimientos científicos, la estadística es la aplicación del conocimiento del cómo se refiere a complementar e inferir la información en los datos de la neblina y realizar inferencias sobre sus significados. (La neblina la podemos imaginar como una nube de entropía, incertidumbre; con el potencial de transformarse en información). Una estadística es un hecho numérico o resumen de análisis de datos. Así que de cierta manera un resumen de datos es el que incluye: tamaño, tasas, desviaciones, tendencias y el cómo se recopiló, manipuló, analizó y se dedujo sobre los hechos numéricos. La neblina puede ser una nube de partículas, una sociedad, el espacio climatológico, reacciones químicas, biológicas o el comportamiento de enjambres, parvadas o corrientes moleculares  en un recipiente. 

Los datos, es una palabra que hace énfasis en la “referencia”, significa algo dado sobre alguna parcela de la realidad y definido por conceptos operativos. Frases como: los datos nos indican; los datos demuestran; los datos muestran; los datos corroboran la teoría. Los datos son señales de algún tipo sobre algo que está fuera de nuestra mente, ese algo que está allí, con independencia y las matemáticas buscan dotarnos de un significado racional sobre eso llamado realidad. El dato tiene significado gracias al cobijo de los hechos. Un hecho es un concepto frontera entre nuestro lenguaje y la realidad, estos conceptos dan el sentido necesario a los datos, que bajo esa semántica categorizan las señales de la realidad. Cuando los datos son procesados por la estadística, se genera un producto estructurado conocido como información. La información es el paso necesario para realizar inferencias (acciones de razonamiento) y al agrupar inferencias, se produce el pensamiento abstracto que da origen al conocimiento.

Las señales de esa neblina llamada realidad, son comúnmente datos numéricos, producto de realizar ensayos de medición. En teoría, si pudiéramos realizar mediciones infinitas sobre algo, los datos significarían una versión precisa de lo que estamos observando. Mediciones infinitas, no es posible realizarlas, ya sea por cuestiones de tiempo, costo y  recursos humanos o tecnológicos. Lo que representan los datos no es la imagen perfecta, no solo por estar impedidos a realizar mediciones infinitas, sino por la propia calidad del dato, toda medición se enfrenta con el error, el ruido e incertidumbre. Sin embargo, los logros asombrosos de la estadística para generar nuevo conocimiento están por todos lados en la vida moderna. Los datos en un principio, antes de ser números fueron señales de palabras, colores, sabores, emociones, sonidos, texturas, concentraciones de químicos, movimiento de partículas en el viento. El control de calidad de fármacos, refrescos, automóviles…, en general todo producto industrial se traduce a números para expresarlo en términos de estructuras de información, es decir, en forma de gráficos, ecuaciones, señales de alerta, frases…

La controversia sobre las estadísticas, radica no en el procesamiento de datos, sino en cómo se utilizan las deducciones para sacar juicios a conveniencia. El papel moderno de la educación es reducir la desconfianza mediante el entendimiento del rigor de la estadística, y justamente advertir que es en la interpretación del resumen estadístico donde hay que poner atención para reconocer si hay justificación para tales inferencias. En muchos casos los reportes de investigación sustentan que comer ciertos alimentos es dañino para la salud humana, basados en juicios estadísticos. Pero el avance científico en mayor detalle dentro de la complejidad biológica pronto desmiente tales aseveraciones, no a la estadística, sino a las inferencias sobre el resumen estadístico. No es de extrañar que este oficio de las inferencias sobre resúmenes estadísticos, genere conflictos de contradicción. 

1.2.1 Datos 

Hemos expresado que los datos son la materia prima de la construcción de estructuras de información, son la base objetiva del resumen estadístico que normalmente se expresa en números. Los datos son el resultado de los hechos, son más que números, son el fruto del análisis conceptual de la teoría, es decir, los números deben asociarse con el significado de los hechos. No hay datos posibles que sean precisos y válidos en su calidad, si estos no están respaldados por conceptos sólidos que se justifiquen en el marco teórico. Además, los datos deben ser en muchos casos vigentes, confiables en el aspecto tecnológico de la medición y el instrumento de registro de su valor verdadero. Otra manera de mirar los datos, es considerarlos como pruebas o evidencias que dan fundamento a ideas y teorías sobre el mundo que nos rodea. Los datos son la conexión con las afirmaciones de nuestras ideas, son los que resquebrajan las viejas ideas e impulsan a las nuevas. Además, los datos no son inmunes a fallas de equipos y límites tecnológicos de los rangos de operación de instrumentos de medición, sin embargo, los datos nos dan certidumbre y tranquilidad sobre nuestras ideas que intentan ser referencia a la verdad en la realidad.

Esto implica que, para ser significativas nuestras ideas y discursos argumentales deben pasar por la verificación objetiva de referencia a los datos. Al comparar nuestros datos con las predicciones podemos confiar o razonablemente abandonar alguna teoría al demostrar su sesgo. Los datos son el camino de exploración a través de este mundo complejo, ellos guían nuestras decisiones sobre los mejores y más prometedores nichos de oportunidad dado el papel de los datos para justificar las ideas y la compresión del mundo.

El origen de la estadística como disciplina académica es relativamente reciente, unos doscientos años. La Royal Statistical Society (1834), sin embargo, antes de su reconocimiento académico, las primeras estadísticas nacieron en el cálculo de probabilidades en juegos de azar, por necesidad de extraer significado razonable de ellos. Otro camino surge al intentar responder a la necesidad de datos estadísticos para tomar decisiones de gobierno en materia militar, económica y cultural. Y es de esta última necesidad que surgió el nombre de estadística: “datos sobre el estado”. Todos los países modernos tienen ahora alguna institución para realizar estudios estadísticos. En el siglo XIX la estadística era un discurso de exploración sobre los datos sociales. Pero es a principios del siglo XX con la pujante Mecánica Cuántica que su cuerpo de conocimiento se desarrolló matemáticamente. Y es en los años 70’s que la estadística se vuelve emocionante al emplear en tiempo real computadoras, potenciando como nadie imaginó una gran cantidad de cálculos de manipulación aritmética que previamente hubieran llevado años, ahora se realizan en minutos. A finales del Siglo XX también se observó la aparición de analistas de datos sobre patrones de grandes volúmenes de datos. Aprender de los datos es sin duda el objetivo de la estadística, es decir, se trata de investigar dentro de lo más complejo de la neblina que llamamos realidad. 

Empresas pequeñas y grandes basan en el control de calidad y  la proyección del futuro de su desempeño en el análisis de sus datos y de los de otros competidores. Estas personas no manipulan símbolos matemáticos y fórmulas, pero están usando herramientas informáticas estadísticas y métodos para obtener conocimiento y entendimiento de la evidencia de los datos. Al hacerlo, necesitan considerar una amplia gama de variables de cuestiones intrínsecamente no matemáticas, tales como la calidad de los datos, cómo fueron recogidos, definir el problema, identificar el objetivo más amplio del análisis y determinar cuánta incertidumbre se asocia con la conclusión.

La estadística es ubicua, se aplica en todos los ámbitos de la vida, esto motivó el desarrollo de métodos nuevos y herramientas estadísticas más específicas. El procesamiento de datos del ADN, partículas subatómicas y redes sociales son solo ejemplos de estos nuevos horizontes de la estadística. Los métodos estadísticos están en la esencia de la investigación científica, en las operaciones industriales, en la administración pública, en la industria, la medicina y otros aspectos de la vida social humana. El desarrollo de alimentos y medicamentos debe pasar por exhaustivas pruebas estadísticas que aseguren la inocuidad del producto y el cumplimiento de la calidad dictada por la normatividad aplicable, antes de estar en el mercado. Dado este papel fundamental, claramente es importante para los ciudadanos educados de esta manera, para ser conscientes de los instrumentos de la toma de decisiones y exploración de lo complejo. Además, la estadística moderna hace uso intensivo de software para procesar los datos, no debe vérsele como manipulación aritmética tediosa de números, este objetivo es fundamental para el interés de las jóvenes generaciones.

El problema con este punto de vista es que puede verse a la estadística como una disciplina de colección de métodos, todos ellos desconectados en la manipulación de números. Por el contrario, es un todo conectado, construido en principios profundamente filosóficos, tal como muchas ciencias lo son. Las herramientas de análisis de datos están vinculadas y relacionadas, algunas pueden incluir a otras herramientas como parte de su estructura. 

Todo comenzó con la definición de dato. Piezas numéricas que describen al universo que estudiamos. Un universo es una parcela de la realidad que es inagotable en su información potencial. Podría ser una mezcla química, un sistema térmico, un sistema mecánico, transacciones de tarjetas de crédito, desempeño de lectura de estudiantes, productividad intelectual de docentes o simples lanzamientos de dados. En ellos no hay nada de particular que modifique la idea de dato. Por supuesto, una colección finita de datos no puede agotar la información contenida sobre algo que es infinito para su descripción. Eso significa que debemos ser cautos de posibles deficiencias o lagunas de los datos. Al capturar los datos debemos además de cuidar su calidad, asegurar que representan los aspectos que apoyan nuestro deseo de sacar alguna conclusión. Al capturar datos nos vemos en la necesidad de eliminar los que son irrelevantes o claramente erróneos. Producir datos está dirigido a objetivos de conocimiento y los aspectos que definen los atributos, características, funciones o aspectos técnicos del objeto de estudio a los que se les suele llamar variables. No solamente se interesa por un objeto de estudio, sino además por las relaciones entre objetos distintos. Muchos no ven los datos como la belleza del mundo, sienten que es como eliminar su poética. Pero los números tienen el potencial para poder percibir esa belleza, esa estética profunda más allá de lo subjetivo, es decir, más allá de nuestros sentidos sensoriales. Sin duda, la estadística es una forma objetiva de revelar lo profundo de sistemas altamente complejos, en los que por pereza intelectual se les suele evadir con salidas como: allí no hay más que desorden, además los números son solo un valor de magnitud. Hemos visto que los números nos dan una interfaz más directa e inmediata a los fenómenos estudiados que el discurso de palabras, porque los datos numéricos normalmente son producidos por instrumentos de mayor confiabilidad que nuestras palabras. Los números proceden de la cosa estudiada, mientras que las palabras son imaginación, los datos son una ventana a través de la lente de instrumentos sofisticados de medición. La propia historia de la tecnología es evidencia del arte de representar la realidad con números referidos a datos. En resumen, mientras simples números constituyen los datos, mirar su relación entre ellos y quizá combinarlos es donde surge la estadística. El análisis estadístico revela la forma en que están distribuidos estos valores.  El valor representativo de la media estadística es un primer indicador de la distribución de datos. 

1.2.2 Estadística descriptiva 

Supongamos que queremos describir la altura de un conjunto de 50 pinos mexicanos. Cincuenta valores de sus alturas representan una vista completa, aunque algo compleja de los árboles. Por lo tanto, necesitamos simplificar (resumir) esta información, pero con una mínima pérdida de detalle. Este tipo de resúmenes se puede lograr de dos maneras generales: podemos transformar los datos numéricos en una forma gráfica (visualizarlos) o podemos describirlos con un conjunto de valores de estadística descriptiva, que resumen las propiedades más importantes de todo el conjunto de datos.

Es uno de los tipos más básicos de la descripción de datos. Es una medida de tendencia central sobre un conjunto de números. Es decir, es el promedio de una lista de números o media aritmética, y se hace más útil si la lista es grande. Para fines de calificación, edad o estaturas nos ayuda a tomar decisiones de en dónde está el grueso de los datos que entenderemos por media estadística o media aritmética. Imagine una tabla con un millón de datos, todos ellos son el mismo número, la media aritmética se calcula más fácilmente sumando el total de los números y dividiendo este resultado entre cuántos son. 

Por ejemplo, las calificaciones de un estudiante en el semestre fueron 7+9+6+4+9+10, suman 45. La media aritmética es un número de un conjunto de números, que se encuentra dividiendo a 45 entre el número total de datos, en este caso es 6. Es 7 1/2. Obtendríamos el mismo resultado si cada una de las 6 evaluaciones fueran 7 1/2, esto sería una distribución de media estadística. 

Donde n es igual al número de datos, y las son cada uno de los datos.

La media aritmética siempre toma un valor entre los valores mayor y menor del conjunto de datos. Por otra parte, equilibra los números en el conjunto, en el sentido de que la suma de las diferencias entre la media aritmética y los valores más grandes, es exactamente igual a la suma de las diferencias entre la media aritmética y los valores más pequeños. En este sentido, es un valor central. La media es la distancia de un tablón desde el extremo a un pivote colocado allí que perfectamente equilibraría el tablón. La media aritmética es una estadística. Esta resume el conjunto de valores en nuestra colección de datos, eso la hace importante.

La mediana por su parte, equilibra el conjunto de otra manera, es el valor tal que la mitad de los números en el conjunto de datos son más grandes y la mitad son menores. Por ejemplo, colocamos los datos en forma creciente del ejemplo anterior 4,5,7,9,9,10; 

la mediana es el promedio de los dos valores centrales =8.

Si n es impar, la mediana es el valor que ocupa la posición (n+1)/2 

Si n es par, la mediana es la media aritmética de los dos valores centrales. 

La mediana es un valor estadístico representativo distinto al valor de la media. Obviamente es más fácil de calcular que la media. Pero en realidad esta ventaja si usamos una computadora, se vuelve irrelevante dado que ella absorbe el tedio de realizar los procesos aritméticos. Para elegir la utilidad de la mediana o la media, dependerá de la precisión de detalle sobre la colección de datos que estemos buscando. Si queremos precisión de la medida central usamos la media.

La media y la mediana, no son los únicos dos resúmenes estadísticos, otro importante es la moda. Es el valor tomado con mayor frecuencia en una muestra. Por ejemplo, para la colección de datos 4,5,7,9,9,10; la moda es 9. Para los datos con una distribución continua, este es el valor correspondiente al máximo local de la densidad de probabilidad. Puede haber más de una valor de moda para una variable, ya que una distribución también puede ser binomial (con dos valores de moda) o incluso polinomio. La moda se define como para todos los tipos de datos. Para los datos continuos normalmente se estima como el centro del intervalo de valor para la barra más alta en un histograma de frecuencia. Si se trata de un distribución polimodal, podemos utilizar las barras con alturas superiores a la altura de barras circundantes. Vale la pena señalar que tal estimación depende de nuestra elección de intervalo en el histograma de frecuencias. El hecho de que podamos obtener un histograma de muestra que tenga múltiples modas (dada la elección de intervalos) no es evidencia suficiente de una distribución polimodal para nuestros valores de población muestreados. 

La media geométrica se define como la la raíz n de un múltiplo de n valores en nuestra muestra (el operador representa la multiplicación):

Por ejemplo si tenemos 5 datos: 950, 1120, 830, 990, 1060. 

La media geométrica se utiliza generalmente para datos en una escala de relación que no contienen ceros y su valor es menor a la media aritmética.

1.2.3 Dispersión

Los promedios, como la media y la mediana, proporcionan un resumen estadístico de un solo número sobre la colección total de los datos. Son útiles porque nos dan los valores numéricos de una tendencia central. Pero esto puede ser engañoso, en particular estos valores individuales pueden diferir sustancialmente de los valores individuales en un conjunto de datos en términos de las distancias respecto a la centralidad media. Es decir, es necesario dar cuenta de lo disperso de los datos alrededor de la media. Los resúmenes estadísticos de dispersión proporcionan esta información. La medida de dispersión más simple es el rango.

El rango se define como la diferencia entre los valores mayor y menor del conjunto de datos. El rango tiene la propiedad de aportar información de la dispersión de los datos, de una manera muy sencilla. Sin embargo, se percibe que no es muy ideal. Después de todo ignora la mayoría de los datos, no puede encontrar el hecho de dónde se encuentra la mayor densidad alrededor de la media. Esta deficiencia se puede superar mediante el uso de una medida de dispersión que toma a todos los valores en cuenta.

Una forma de hacer esto, es tomar la diferencia entre la media aritmética y cada número del conjunto de datos al cuadrado y luego encontrar la media de estas diferencias cuadradas. Si la media resultante de las diferencias cuadradas es pequeña, nos dice que, en promedio los números del conjunto no son demasiado diferentes de su promedio. Es decir, ellos no son muy dispersos. Esta medida de la diferencia de cuadrados se llama varianza de los datos o desviación cuadrada media. 

Una complicación surge del hecho de que la varianza implica al valor del cuadrado de los datos. La varianza es una media de los valores cuadrados. Si medimos la productividad de páginas escritas, estamos hablando del promedio de páginas cuadradas. Es obvio que no hacemos esto. Debido a esta dificultad, es común tomar la raíz cuadrada de la varianza. Esto cambia las unidades, a las unidades originales y produce la media de dispersión llamada desviación estándar. A la media se le suele conocer también como esperanza matemática, es el valor medio esperado E.  

Varianza

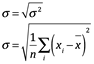Desviación estándar 

La desviación estándar supera el problema que identificamos con el rango, al emplear todos los datos. Esta desviación típica, si la mayoría de los datos están agrupados muy cerca, con pocos periféricos, se reconocerán por la desviación estándar pequeña. Por  el contrario, si los datos toman valores muy lejanos de la esperanza matemática, los valores de la desviación estándar serán mucho mayores.

1.2.4 Oblicuidad

Si bien, las medidas de dispersión nos dicen cuánto se desvían los valores individuales de datos unos de otros, no nos dicen de qué manera se desvían. En particular, no nos dicen si las desviaciones más grandes tienden a ser los valores más grandes o los valores más pequeños del conjunto de datos. Para detectar esta diferencia, necesitamos de otro resumen estadístico, uno que recoge y mide la asimetría en la distribución de valores de los datos. Un tipo de asimetría de valores se llama sesgo. Las distribuciones sesgadas son comunes. Un ejemplo clásico es la distribución de la riqueza en la sociedad, en la que la mayoría de las personas está en valores pequeños y unos cuantos en valores mayores de riqueza. Es justo por lo dispar de los sueldos. El sesgo es un estimador entre la diferencia de su media y el valor numérico del parámetro que se estima dentro de un conjunto de datos.

También se conoce como medidas de la ubicación de la distribución de datos. Interpretar el término “promedio” como el punto medio del lugar es una mala aprensión. Esto se debe a que desgraciadamente cuando se informa un promedio en los medios de comunicación, a menudo no está claro si esto debe interpretarse como la media o la mediana. No es suficiente dar un solo resumen de los datos para una distribución, necesitamos tener una idea de la propagación, a veces conocida como variabilidad. Una visión de variabilidad estadística incluye tres modos clásicos. El rango, que es una opción natural, pero claramente muy sensible a valores extremos. En contraste, el rango intercuartil IQR no se ve afectado por los extremos. Finalmente la desviación estándar es una medida de propagación ampliamente utilizada. Es la medida técnicamente más compleja, pero solo es realmente adecuada para los datos simétricos bien comportados que también está influenciada por los valores periféricos. Esto demuestra que los datos a menudo tienen algunos errores, valores atípicos y otros valores extraños, pero esto no necesariamente necesita ser identificado y excluido individualmente. 

Esto muestra que no podemos mirar los datos en su valor simplemente describiendo las diferencias entre grupos de números. Grandes colecciones de datos numéricos se resumen y comunican rutinariamente usando algunas estadísticas de ubicación y propagación, y se ha demostrado que estos no pueden llevarnos un largo camino en la comprensión de un patrón general. Para ello, es necesario una descripción de las relaciones entre variables. Es conveniente utilizar un solo número para resumir una relación de constante aumento o diminución entre pares de números que se muestran en una gráfica de dispersión. Este es generalmente elegido para ser el coeficiente de correlación de Pearson, una idea originalmente propuesta por Francis Galton pero, publicada por Karl Pearson en 1895, uno de los fundadores de las estadísticas modernas^[7].

Una correlación de Pearson se ejecuta entre -1 y 1, y expresa cuán cerca de una línea recta caen los puntos o datos. Cuanto más intensa sea la concordancia (en sentido directo o inverso) de las posiciones relativas de los datos en dos variables, el producto del numerador toma mayor valor (en sentido absoluto). Si la concordancia es exacta, el numerador es igual a N (o a -N), y el índice toma un valor igual a 1 (o -1).

donde , son la desviación estándar de la variable x y y respectivamente.

La covariación , es el grado de concordancia de las posiciones relativas de los datos de dos variables. En consecuencia, el coeficiente de correlación de Pearson opera con puntuaciones tipificadas (que miden posiciones relativas), se define:

Una correlación de 1 ocurre si todos los puntos se encuentran en una línea recta que va hacia arriba, mientras que se produce una correlación de -1 si todos los puntos se encuentran en una línea que va hacia bajo. Una correlación cercana a 0 puede provenir de una dispersión aleatoria de puntos, o cualquier otro patrón en el que no hay una tendencia sistemática hacia arriba o hacia abajo, algunos ejemplos se muestran en la figura siguiente.

Figura 1.2 Patrón de coeficiente de correlación  

Una medida alternativa se llama rango de correlación Spearman, por el psicólogo Charles Spearman, quien desarrolló la idea en una inteligencia subyacente, y depende de las filas de datos en lugar de valores específicos. Esto significa que pueden estar cerca de -1 o 1 si los puntos están cerca de una línea que aumenta o disminuye constantemente, incluso si esta línea no es recta^[8]. 

donde D es la diferencia entre los correspondientes estadísticos de orden de x - y. N es el número de parejas de datos.

Figura 1.3 El coeficiente de correlación de Spearman es menos sensible que el de Pearson para los valores muy lejos de lo esperado. En este ejemplo: Pearson = 0.30706 Spearman = 0.76270

Los coeficientes de correlación son simplemente resumen de asociación, y no se pueden utilizar para concluir que definitivamente hay una relación subyacente entre variables. En muchas aplicaciones el eje x representa una cantidad conocida como la variable independiente y el interés se centra en su influencia en la variable dependiente trazada en el eje y. Este coeficiente aún requiere estudiar más a fondo la causalidad. 

Describir tendencias. Se emplea para contestar preguntas como, ¿Cuál es el patrón de crecimiento de la población mundial en el último siglo? La población del mundo está aumentando y comprender los impulsos del cambio demográfico es de vital importancia para prepararse para los desafíos que enfrentaremos en el futuro. La ONU elabora estimaciones del recuento de todos los países del mundo desde 1951, junto con proyecciones útiles al año 2100^[9]. Utiliza un resumen sencillo de la tendencia de cada país, en el que un aumento de 4 significa que en el 2015 hay cuatro veces más personas que en 1951. Siempre es valioso dividir los datos de acuerdo con un factor, en este caso en continentes, que explica parte de la variabilidad general. Los grandes aumentos en África se destacan, ya que hay una amplia variación en países como Costa de Marfil, que representa un caso extremo. Asia también demuestra una enorme variación, lo que refleja la amplia diversidad de países en esos continentes, con Japón y Georgia en un extremo y Arabia Saudita en el otro, con el mayor aumento reportado en el mundo. Los aumentos en Europa han sido relevantemente bajos. Como cualquier gráfico, eso plantea más preguntas y fomenta una mayor exploración, tanto en términos de identificación de países individuales, como, por supuesto, examinando las proyecciones de las tendencias futuras.

Es evidente que hay un gran número de formas de examinar un conjunto de datos tan complejo como las cifras de población de la ONU. Sin embargo, Alberto Cairo ha identificado cuatro características comunes de una buena visualización de datos^[10]:

1. Contener información confiable.

2. El diseño ha sido elegido para que los patrones relevantes se vuelvan notables.

3. Se presentan de una manera atractiva, pero la apariencia no debe minar el camino de la honestidad, claridad y profundidad.

4. Cuando sea apropiado, se organiza de una manera que permita cierta exploración a las implicaciones.

La cuarta característica se puede facilitar permitiendo que el público interactúe con la visualización, como los sistemas que dispone Mathematica en línea, ver URL: https://www.wolfram.com/language/elementary-introduction/2nd-ed/preface.html.es 

Pero a menudo la pregunta va más allá de la simple descripción de los datos. Queremos aprender algo más grande que las observaciones que tenemos delante, ya sea para hacer predicciones o decir algo más básico ¿Por qué están aumentando los números?

Una vez que queremos empezar a generalizar a partir de los datos, aprendemos algo sobre el mundo de nuestras observaciones inmediatas, tenemos que hacernos la pregunta ¿Aprender sobre qué? Y esto nos obliga a confrontar la difícil idea de la inferencia inductiva.

Muchas personas tienen una vaga idea de la deducción, gracias a Sherlock Holmes usando razonamiento deductivo cuando implica a un sospechoso de un crimen. En la vida real, la deducción es el proceso de utilizar las reglas de la lógica fría para trabajar desde las premisas generales hasta conclusiones particulares. Pero la inducción funciona de otra manera, al tomar casos particulares y tratar de llegar a conclusiones generales. La distinción crucial es que la deducción es lógicamente cierta, mientras que la inducción es generalmente incierta desde el punto de vista lógico y no en relación a lo que hay de conexión con lo real. 

Por supuesto que sería ideal si pudiéremos pasar directamente de mirar los datos sin procesar a hacer afirmaciones generales sobre la población objetivo. En los cursos de estadística estándar, se supone que las observaciones se extraen aleatoria  y directamente de la población de interés. Pero esto rara vez es el caso en la vida real, y por lo tanto, tenemos que considerar todo el proceso de pasar de los datos sin procesar a nuestro objetivo final. 

Etapas 

1. Los datos brutos registrados sobre los números de las variables.

2. El tamaño de muestra que nos dice algo sobre…

3. Datos de la potencial muestra en el estudio de…

4. Inferencias sobre la población objetivo.

Pasando de los datos (Etapa 1) a la muestra (Etapa 2), estos son problemas de medición, ¿es lo que registramos en nuestros datos un reflejo preciso de lo que nos interesa? Deseamos que nuestros datos sean:

• Fiables, en el sentido de tener una razonable baja variabilidad de un caso a otro. 
• Válidos, en el sentido de medir lo que realmente quieres medir, y no tener un sesgo sistemático. 

Por ejemplo, en los ajustes finos en encuestas, la calidad de la encuesta también requiere que los entrevistadores sean honestos cuando reportan su actividad, no exagerar o restar importancia a sus experiencias. Una encuesta no es válida si está sesgada en una particular respuesta. Las respuestas a las preguntas también pueden verse influenciadas por lo que se ha hecho de antemano, un proceso conocido como cebado, un carácter autoinforme de la encuesta voluntaria, y el hecho de que la pregunta sea precedida por cuestiones que alteran el sentido de objetividad. 

Pasando de la muestra (Etapa 2) al estudio de la población (Etapa 3), esto depende de la calidad fundamental del estudio, también conocido como validez interna, ¿refleja con precisión la muestra que observamos lo que está pasando en el grupo que realmente estamos estudiando? Aquí es donde llegamos a la manera crucial de evitar el sesgo: muestreo aleatorio. George Gallup, que esencialmente inventó la idea de la encuesta de opinión en la década de 1930, se le ocurrió una fina analogía para el valor del muestreo aleatorio^[11]. Dijo que si usted ha cocinado una gran sartén de sopa, no es necesario comer todo para averiguar si necesita más condimento. Usted puede simplemente probar una cucharada, siempre que le haya dado un buen gusto. Una prueba literal de esta idea fue proporcionada por la lotería para reclutamiento en la guerra de Vietnam de 1969, que tuvo que proporcionar una lista de edades y prepararon cápsulas para contener los registros, estos destinados al azar fueron continuamente revueltos y extraídos de las cápsulas. 

El hecho que tengamos masas de datos no necesariamente ayuda a garantizar una buena muestra e incluso puede dar falsa seguridad. Lo representativo está en lo aleatorio. 

Pasando de la población estudiada (Etapa 3), a la población objetivo (Etapa 4) finalmente, incluso con una medición perfecta y una muestra aleatoria meticulosa, los resultados todavía pueden no reflejar lo que queríamos investigar en primer lugar si no hemos sido capaces de preguntar a las personas en las que estamos particularmente interesados en encuestas. Queremos que nuestro estudio tenga validez externa. Por ejemplo, llevar ensayos clínicos en hombres adultos, cuando el medicamento potencial se utiliza en niños y mujeres embarazadas. Nos gustaría conocer los efectos en todos, pero esto no puede resolverse solo con análisis estadístico, inevitablemente necesitamos hacer inferencias y ser muy cautelosos.

Cuando tenemos todos los datos. Aunque las ideas de aprender de los datos se ilustra cuidadosamente mirando encuestas, de hecho gran parte de estos datos no se basan en muestreo aleatorio, o de hecho en cualquier muestreo. Los datos recopilados rutinariamente Big Data, de compras en línea, de transacciones sociales, la productividad académica. En estas situaciones tenemos todos los datos disponibles. En cuanto al proceso de inducción no hay brecha entre las etapas 2 y 3. La muestra y la población del estudio son esencialmente las mismas. Esto evita cualquier preocupación acerca de tener un tamaño de muestra adecuado, pero muchos otros problemas todavía pueden permanecer. 

Cuando tenemos todos los datos, es sencillo producir estadísticas que describan lo que se ha medido. Pero cuando queremos utilizar los datos para sacar conclusiones más amplias sobre lo que está sucediendo alrededor, entonces la calidad de los datos se vuelve primordial, y tenemos que estar alerta al tipo de sesgo sistemático que pueden poner en peligro la fiabilidad. 

La curva en forma de campana. Ya hemos discutido el concepto de una distribución de datos, como el patrón que hacen los datos, a veces conocido como la distribución empírica o distribución de muestra. A continuación, debemos abordar el concepto de una distribución de la población, el patrón en todo el grupo de interés. Considere que una mujer mexicana acaba de dar a luz. Podríamos pensar que su bebé ha sido registrado, como una especie de muestra de una sola persona, de toda la población de bebés recién nacidos de mujeres hispanas en Canadá. Su raza es importante, ya que los pesos al nacer se reportan dependiente de las diferentes razas. La distribución de la población es el patrón hecho por los pesos al nacer de todos estos bebés, aunque este no es todo el universo de bebés contemporáneos, es una muestra tan grande que podemos tomarla como la población. Su posición en la distribución se puede considerar para evaluar si su peso es “inusual”. La forma de esta distribución es importante. Pueden considerarse cantidades continuas cuya distribución de la población es suave. El ejemplo clásico es la curva de campana o distribución normal. Explorada por primera vez por Friedrich Gauss en 1809 en el contexto de errores de medición en astronomía y topografía. La teoría muestra que se puede esperar que la distribución normal ocurra para fenómenos que son impulsados por un gran número de pequeñas influencias, por ejemplo,  rasgos físicos complejos que no están influenciados por unos pocos genes. 

La distribución normal se caracteriza por su media o expectativa, y su desviación estándar, que como hemos visto es una medida de dispersión, estos se reconocen como parámetros de descripción de poblaciones. Una población puede ser considerada como un grupo físico de individuos, pero también como la distribución de probabilidad para observaciones aleatorias. Esta doble interpretación será fundamental cuando lleguemos a una inferencia estadística formal. 

1.2.5 ¿Qué es una población?

Las etapas de inducción anteriores funcionan muy bien con encuestas planificadas, pero una gran cantidad de análisis estadísticos no encajan tan fácilmente en este marco. Se ha visto que, especialmente cuando utilizamos registros administrativos, policiacos sobre delitos, podemos tener todos los datos posibles. Pero aunque no haya muestreo, la idea de una población subyacente todavía puede ser valiosa. Aunque la idea de una población se establece casualmente en los cursos de estadística, hay ejemplos de otra idea sofisticada que vale la pena explorar con cierto detalle, ya que muchas ideas importantes se basan en este concepto. Hay tres tipos de poblaciones de las que se puede extraer una muestra, ya sea que los datos provengan de personas, transacciones, árboles, moléculas o cualquier otra cosa.

Una población literal. Este es un grupo identificable, como cuando elegimos una persona al azar al sondear. O puede haber un grupo de individuos que podrían ser medidos, y aunque en realidad no fueron elegidos al azar, tenemos datos de voluntarios. Por ejemplo, podríamos considerar a las personas que adivinaron el número de gomitas dentro de un frasco, como la muestra de la población de los estudiantes de matemáticas para un estudio. 

Una población virtual. Con frecuencia tomamos medidas usando un dispositivo, como tomar la presión arterial o medir la Humedad relativa. Sabemos que siempre podríamos tomar más medidas y obtener una respuesta ligeramente diferente, ya que sabrá si alguna vez ha tomado mediciones repetitivas, por ejemplo de la presión arterial. La cercanía de las múltiples lecturas depende de la precisión del dispositivo y la estabilidad de las circunstancias, podríamos pensar en esto como extraer observaciones de una población virtual de todas las mediciones que podríamos tomar si tuviéramos suficiente tiempo. 

Una población metafórica. Cuando no hay una población más grande en lo absoluto. Es un concepto inusual. Aquí actuamos como si el punto de datos se extrajera de alguna población al azar, pero claramente no lo es, como con los niños que se someten a una cirugía, no hicimos ningún muestreo, tenemos todos los datos y no hay más que pudiéramos  recopilar. Piense en el número de asesinatos que ocurren cada año, los resultados del examen para una clase en particular, o los datos sobre todos los países del mundo, ninguno de ellos puede ser considerado como una muestra de una población real. 

La idea de una población metafórica es desafiante, y puede ser mejor pensar en lo que hemos observado, como haber sido extraída de algún espacio imaginario de posibilidades. Por ejemplo, la historia de la humanidad es lo que es, pero podemos imaginar que la historia ha partido de manera diferente, y resulta que hemos terminado en una de estas posibilidades de los estados del mundo. Este conjunto de todas las historias posibles puede considerarse una población metafórica. 

Es evidente que pocas aplicaciones de la ciencia estadística implican realmente un muestreo aleatorio literal, y que es cada vez más común tener todos los datos que están potencialmente disponibles. Sin embargo, es extremadamente valioso mantener la idea de una población imaginaria de la que se extrae nuestra muestra, ya que entonces podemos utilizar todas las técnicas matemáticas que se han desarrollado para el muestreo de poblaciones reales. 

1.3 ¿Qué causa qué? 

¿Es causal de mi cobardía, mediocridad…, abandonar un libro justo en la primera página? Cuando razonar en la universidad se reflexiona, ¿es riesgo de tumor cerebral?  

“La epistemología es el estudio de cómo y por qué se producen las enfermedades en la población”. Un estudio ambicioso en miles de hombres y mujeres; informa que los hombres con una posición económica más alta tenían tasa ligeramente mayor de ser diagnosticados con un tumor cerebral. Los noticieros consideran que sería mejor presentarlo diciendo: “los altos niveles de educación están vinculados a un mayor riesgo de tumor cerebral^[12]”. A pesar de que claramente el estudio está dirigido al concepto operativo de nivel socioeconómico y no a la educación. Estamos en un mundo de posverdad, para cualquiera que haya pasado mucho tiempo acumulando intelecto académico, este titular podría en el noticiero resultar muy alarmante. Pero, ¿deberíamos preocuparnos? Este es un gran estudio elegante basado en un registro de la población completa, no es una muestra, por lo que podemos concluir con confianza, que en realidad se encontraron un poco más de tumores cerebrales en personas más educadas. Pero, ¿todo ese esfuerzo leyendo y escribiendo al parecer sobrecalentaba el cerebro y condujo a algunas extrañas mutaciones celulares? A pesar del titular del periódico, lo dudamos mucho. Y para darles crédito, los propios autores expresaron: “la integridad del registro y el sesgo de detección del cáncer son posibles explicaciones de los hallazgos^[13]”. En otras palabras, las personas ricas con educación superior son más propensas a ser diagnosticadas y registradas con un tumor, un ejemplo de lo que se conoce como sesgo de determinación en epidemiología.

La correlación no implica causalidad, sabemos que el coeficiente de correlación de Pearson mide cuán cerca están los puntos en una gráfica de dispersión a una línea recta. Al considerar los hospitales mexicanos que atendieron COVID-19 en 2020, e entubaron los pacientes a respiradores artificiales. Se traza el número de casos contra su supervivencia, la alta correlación mostró que los hospitales más grandes estaban asociados con una menor mortalidad. Pero no se pudo concluir que los hospitales más grandes causaron la menor mortalidad. Esta es una utopía, como ejemplo.

Esta actitud cautelosa tiene una larga tradición intelectual. Cuando el coeficiente de correlación recién desarrollado por Karl Pearson estaba siendo discutido por un comité de revisores de la revista Nature en 1900, alguien advirtió que la correlación no implica causalidad. En el siglo siguiente esta frase ha sido un mantra repetidamente pronunciado por los estadísticos cuando en las aulas universitarias enseñan a ser cautos a los estudiantes con la afirmación basada en observación de dos cosas o más que tienden a viajar juntas. Incluso hay un sitio web que genera automáticamente asociaciones tan idiotas como las que expresamos en estas líneas a la ligera^[14]. 

Parece haber una profunda necesidad humana de explicar cosas que suceden en términos de simples causas -relaciones de efecto- estamos seguros de que todos contribuimos un poco a construir mitos urbanos. Incluso hay una palabra para la tendencia a construir razones para una conexión entre lo que en realidad son eventos no relacionados -apofenia- con el caso más extremo cuando la simple desgracia se explica por la mala suerte, mala voluntad de los demás, o el cisne negro, un Déjà vu o error en la Matrix; o incluso brujería. 

Desafortunadamente o tal vez, porque la educación es tan mediocre, el mundo es un poco más complicado que la simple conspiración de un genio malvado, como lo pensó Descartes. Y la primera complicación viene en tratar de averiguar lo que queremos decir con “porque”.

¿Qué es la causalidad? Es un tema profundamente cuestionado, que tal vez es sorprendente, ya que parece bastante simple en la vida real: hacemos algo, y eso conduce a otra cosa. Me martillé un dedo y ahora me duele. Pero, ¿cómo sabemos que mi pulgar no me habría dolido de todos modos? Tal vez podamos pensar en lo que se conoce como un contrafactual. Si no hubiera martillado mi pulgar con el martillo, entonces no me dolería esta tarde. Pero esto siempre será una suposición, que requiere la reescritura de la historia, ya que nunca podemos saber realmente con certeza lo que podría haber sucedido, aunque estamos “muy seguros” que no nos dolería el pulgar por propia voluntad. 

Esto se vuelve aún más complicado cuando permitimos la inevitable variabilidad que subyace a todo lo interesante en la vida real. Capas subyacentes de la realidad, con independencia causal, teórica y empírica, entre lo atómico, lo molecular, lo genético, lo bioquímico, lo literario, lo cognitivo, lo gramatical, lo poético, la música, las matemáticas…, con el causal de que nuestra novia nos deje por otra persona. Por qué los científicos tardaron tanto tiempo en realizar una hipótesis deductiva entre fumar y el cáncer de pulmón; entre la violencia cruel y el bajo consumo de literatura. Por qué la mayoría de los que fuman no tienen cáncer de pulmón, y algunas de las que no fuman si lo tienen. Por qué las personas realizan actos criminales de asesinato y son grandes lectores de libros clásicos. Todo lo que podemos decir, es que es más probable tener cáncer si fumas que si no fumas, pero por qué tomó tanto tiempo a las leyes su prohibición y restringir la edad para comprar tabaco es una muestra de que el conocimiento proveniente de datos requiere ser reconocido.

Así que nuestra idea de “estadística” de causalidad no es estrictamente determinista. Cuando decimos que X causa Y, no queremos decir que cada vez que ocurre X, entonces Y también. O que Y solo ocurrirá si se produce X. Simplemente queremos decir que si intervenimos y forzamos X a ocurrir, entonces Y tiende a suceder más a  menudo. Así que nunca podemos decir que X causó Y en un caso específico, solo que X aumenta la proporción de veces que sucede Y. Esto tiene dos consecuencias vitales para lo que tenemos que hacer si queremos saber lo que causa qué. En primer lugar, para inferir la causalidad con verdadera confianza, lo ideal es intervenir y realizar experimentos controlados. En segundo lugar, dado que se trata de un mundo estadístico o estocástico (aquel cuyo comportamiento no es determinista), tenemos que intervenir acumulando evidencia.

Los ejemplos de correlación del tumor-intelecto, muerte COVID-tamaños de hospital, reducción de la violencia-consumo de literatura; solo pueden ser tomados en serio si cuentan con el respaldo de nueva evidencia en el largo plazo, tal como la correlación tabaco-cáncer de pulmón. 

Y eso nos lleva naturalmente a un tema delicado: realizar experimentos en un numeroso grupo de sujetos y objetos. Pocos de nosotros podríamos disfrutar de la idea de ser conejillos de laboratorio, especialmente cuando la vida y la muerte están presentes como opciones. Lo que hace que sea aún más notable que miles de personas han estado dispuestas a ser parte de grandes estudios científicos en los que ni ellos ni sus médicos sabían qué tratamiento terminaría recibiendo un saldo positivo. El hecho de que hay esperanza de éxito lo fue todo.

Quizá en buena medida las noticas falsas, son el reflejo de su éxito, la realidad de una educación que no enseña a pensar, sino a gritar, soy libre, pero inculto.  

El objetivo de los ensayos experimentales es llevar a cabo demostraciones justificadas que determinen adecuadamente la causalidad y estime el efecto medio de un nuevo contra efecto, en el caso clínico debería obedecer a controles, ignorando la posibilidad de que cualquier relación observada no es causal en lo absoluto, es decir, nada en ensayo experimental es resultado de la casualidad. 

En la práctica, el proceso de asignación del tratamiento controlado en los ensayos experimentales, es generalmente más complejo que lo simple  aleatorio, caso por caso, se asegura que los tipos de sujetos estén igualmente representados. Esta idea surgió de los experimentos agrícolas aleatorios impulsado por Ronald Fisher^[15]. Un campo grande se divide en parcelas individuales, y luego a cada parcela se le asigna aleatoriamente fertilizantes diferentes, al igual que con las personas se les asigna un tratamiento al azar. Pero partes del campo podrían ser sistemáticamente diferentes debido al drenaje, la sombra, y así sucesivamente, y por lo tanto, primero el campo se dividiría en “bloques” que contienen parcelas que resultarían más o menos similares. La aleatorización se organiza entonces de una manera que garantice que cada bloque contendrá el mismo número de parcelas dados a cada fertilizante, lo que significaría, digamos, que los tratamientos estaban equilibrados dentro de las zonas de tipo de suelo similar. 

La principal innovación en experimentación aleatoria se refiere a las pruebas “A/B” en el diseño web, en las que los usuarios están (sin saberlo) dirigidos a diseños alternativos para páginas web, y mediciones realizadas sobre el tiempo invertido en las páginas, clics en enunciados, tiempo de lectura… Una serie de pruebas A/B pueden conducir rápidamente a un diseño optimizado, y los enormes tamaños de muestra significan que incluso los efectos pequeños, pero potencialmente rentables, se pueden detectar de forma confiable. Esto ha significado que una comunidad completamente nueva ha tenido que aprender a hacer comparaciones múltiples.

1.4 ¿Qué hacemos cuando no podamos aleatorizar? 

Es fácil para los investigadores aleatorizar si todo lo que tienen que hacer es cambiar un sitio Web: no hay esfuerzo para reclutar ya que ni siquiera saben qué son los sujetos de un experimento y no hay necesidad de obtener la aprobación ética para usar su comportamiento dentro de las estructuras de contenido. Pero la aleatorización es  a menudo difícil y a veces  imposible, no podemos probar el efecto de nuestros hábitos al aleatorizar a las personas. Cuando los datos no surgen de un experimento, se dice que son observacionales. Tan a menudo nos quedamos con el mejor esfuerzo posible para ordenar la correlación de la causalidad mediante el uso de un buen diseño experimental y principios estadísticos aplicados a los datos observacionales, combinados con una dosis saludable de escepticismo.  

¿Qué hacer si se observa una asociación de cosas y eventos?

Aquí es donde se requiere cierta imaginación estadística, y es un ejercicio agradable para adivinar las razones por las cuáles una correlación observada podría ser falsa. Algunas son fáciles por la estrecha correlación entre crema de coco y los ingenieros civiles, presumiblemente porque ambas medidas aumentaron con el tiempo. Del mismo modo, cualquier correlación entre las ventas de teclados y el dolor estomacal se debe a que ambos efectos están influenciados por el clima. Cuando una aparente asociación entre dos resultados puede explicarse por algún factor común observado que influye en ambos, esta causa común se conoce como un confundidor: son potenciales factores que pueden ser registrados y considerados en un análisis por su aparente referencia a los hechos.

La técnica más simple para tratar con confundidores es mirar matemáticamente la relación aparente dentro de cada nivel del factor. Esto se conoce como ajuste o estratificación. Así, por ejemplo, podríamos explorar la relación entre los ahogamientos y las ventas de helados en días con aproximadamente la misma temperatura. 

Pero el ajuste puede producir algunos resultados paradójicos. En 1996, la tasa de aceptación general para estudiar cinco asignaturas académicas en Cambridge fue ligeramente mayor para los hombres (24% de 2.470 solicitantes) que para las mujeres (23% de 1.184 solicitudes). Los temas estaban todos en lo que hoy se conoce como temas STEM (ciencia, tecnología, ingeniería y medicina), que históricamente han sido estudiados predominantemente para hombres. ¿Se trata de un caso de discriminación de género? Esto se conoce como efecto Yule-Simpson o paradoja de Simpson^[16], que ocurre cuando la dirección aparente de una asociación se invierte ajustándose para un factor de confusión, que requiere un cambio completo en la elección aparente de los datos. Los estadísticos se deleitan en encontrar ejemplos de esto en la vida real^[17], cada uno reforzando aún más la precaución necesaria para interpretar los datos de nuestras observaciones^[18]. 

“Paradoja Simpson, es una paradoja en la cual una tendencia que aparece en varios grupos de datos desaparece cuando estos grupos se combinan y en su lugar aparece la tendencia contraria para los datos agregados. Esta situación se presenta con frecuencia en las ciencias sociales, en los experimentos de André y en la estadística médica,? y es causa de confusión cuando a la frecuencia de los datos se le asigna sin fundamento una interpretación causal.? La paradoja desaparece cuando se analizan las relaciones causales presentes^[19]”.

En Inglaterra se dan avalúos de las casas en la correlación entre precios de la casa y la cercanía de los centros comerciales, particularmente los de lujo^[20]. La correlación casi con toda seguridad refleja la política de abrir tiendas en lugares más ricos, y por lo tanto es un buen ejemplo de que la cadena de causalidad es precisamente opuesta de lo que se ha reclamado de que mayores consumidores es lo deseable. Esto se conoce, como era de esperar, como causalidad inversa. Se producen ejemplos más serios en estudios que examinan la relación entre consumo de alcohol y los resultados de salud, que generalmente encuentran que los no bebedores tienen tasas de mortalidad sustancialmente más altas que los bebedores moderados. ¿Como puede tener esto sentido dado el impacto del alcohol, por ejemplo en el hígado? Esta relación se ha atribuido parcialmente a la causalidad inversa, aquellas personas que son más propensas a morir no beben porque ya están enfermas (posiblemente a través del consumo excesivo de alcohol en el pasado). Los análisis más cuidadosos  ahora excluyen a los ex bebedores, y también  ignoran los acontecimientos adversos de salud en los primeros años del estudio, ya que estos pueden deberse a condiciones preexistentes^[21]. Incluso con estas exclusiones, algunos beneficios generales para la salud para el consumo moderado de alcohol parecen permanecer, aunque está profundamente cuestionado^[22]. 

¿Podemos concluir la causalidad a partir de datos observacionales?

El destacado estadístico Austin Bradford Hill, estableció los estándares para confirmar el vínculo entre el tabaquismo y el cáncer de pulmón^[23]. Antes de asegurar que una exposición y un resultado era causal, se tenían que revisar los criterios sobre la evidencia directa, mecanicista y paralela^[24].

Evidencia directa:

1. El tamaño del efecto es tan grande que no puede explicarse por la confusión plausible.

2. Hay proximidad temporal y/o espacial apropiada, ya que la causa precede al efecto y el efecto ocurre después de un intervalo plausible, y/o la causa ocurre en el mismo sitio que el efecto.

3. La capacidad de respuesta y reversibilidad de la dosis: el efecto aumenta a medida que aumenta la exposición, y la evidencia es aún más fuerte si el efecto se reduce. Tras la reducción de la dosis.

Evidencia mecanicista:

4. Existe un mecanismo de acción plausible, que podría ser biológico, químico o mecánico, con evidencias externas de una cadena causal.

Evidencia paralela:

5. El efecto encaja con lo que hoy se conoce.

6. El efecto se encuentra cuando se replica el estudio.

7. El efecto se encuentra en estudios similares, pero no idénticos.

Estas directrices pueden permitir que la causalidad se determine a partir de evidencias anecdóticas, incluso en ausencia de un ensayo aleatorio. Por ejemplo, se han observado úlceras bucales después de que se frota aspirina dentro de la boca, por ejemplo para aliviar el dolor dental. El efecto obedece a la directriz, ocurre donde se frota, es una respuesta plausible a un compuesto ácido, esto no es contradictorio a lo reportado por la ciencia actual y es similar al efecto conocido de la aspirina sobre el desarrollo de la úlcera estomacal,  por lo que es razonable concluir que esto es una reacción adversa genuina al fármaco. 

Estos criterios de Bradford Hill se aplican a las conclusiones científicas generales de las poblaciones. Pero también podemos tomar casos individuales, por ejemplo, en un litigio de responsabilidad laboral causada por riesgo de trabajo. Nunca se puede establecer con absoluta certeza que algo fue la causa por ejemplo de cáncer; ya que no se puede demostrar que el cáncer no se hubiera producido sin la exposición. Sin embargo, algunos tribunales han aceptado que, en el equilibrio de probabilidades, se ha establecido que la relación de causalidad directa sobre el riesgo relativo asociado a la explosión de algo es superior a 2 %. ¿Por qué dos? Presumiblemente el razonamiento detrás de esta conclusión es que:

1. Supongamos que, en el funcionamiento normal de las cosas, de 1,000 hombres, 10 tendrían cáncer de pulmón. Si el asbesto duplica más el riesgo, si estos 1,000 hombres hubieran estado expuestos al asbesto, entonces tal vez 25 habrían desarrollado cáncer de pulmón.

2. Por lo tanto, de las personas expuestas al asbesto no desarrollan cáncer de pulmón si no hubieran estado expuestas. 

3. Así que, más de la mitad de los cánceres de pulmón en este grupo habrán sido causados por el asbesto. 

4. Un sujeto de este grupo de personas, entonces en el equilibrio de probabilidades su cáncer de pulmón fue causado por el asbesto.

Este tipo de argumento ha llevado a una nueva área de estudio conocida como epidemiología forense, que trata de utilizar evidencia derivada de poblaciones para sacar conclusiones sobre lo que podría haber causado eventos individuales. En efecto, esta disciplina ha sido forzada a existir por personas que buscan comprensión, pero esta es una área muy difícil para el razonamiento estadístico sobre la causalidad. 

El manejo adecuado de la causalidad sigue siendo impugnado en el ámbito de las estadísticas, ya se trate de productos farmacéuticos, alimentos…, sin aleatorización, es raro poder sacar conclusiones seguras. Un enfoque imaginativo por ejemplo aprovecha que en muchos objetos de estudio está presente el hecho, por ejemplo como en los genomas, donde muchos genes se propagan esencialmente al azar a través de la población, por lo que es como si nos hayamos aleatorizado a nuestra versión específica en la confección de aleatorio. Esto se conoce como aleatorización Mendeliana^[25]. 

Se han desarrollado otros métodos estadísticos avanzados para tratar de ajustar a los posibles confundidores, y así, acercarse a una estimación del efecto real de la exposición a algo, y estos se basan en gran medida en la idea importante del análisis de regresión. Y por eso debemos reconocer, una vez más, la fértil imaginación de Francis Galton^[26]. 

1.5 Modelado de relaciones mediante regresión

Las ideas aquí desarrolladas, ya nos colocan en la posibilidad de visualizar asumir un único conjunto de números, y también mirar las asociaciones entre pares de variables. Estas técnicas básicas pueden llevarnos a un camino notablemente largo de especialización, pero los datos modernos generalmente serán mucho más complejos. A menudo, habrá una lista de variables posiblemente relacionadas, una de las cuales estamos particularmente interesados en explicar o predecir, si el riesgo de algo para un individuo o población produce, por ejemplo, cáncer, demencia… Para ello es necesario un modelo estadístico de relación formal entre variables, que podemos utilizar para explicar o predecir. Eso significa inevitablemente introducir algunas ideas matemáticas, pero los conceptos básicos deben ser claros sin usar cálculos de álgebra.

Pero primero volvamos a Francis Galton. Tenía el interés obsesivo del clásico caballero victoriano científico en recopilar datos y obtener la sabiduría, por ejemplo, sobre el peso de un buey. Utilizó sus observaciones para hacer pronósticos meteorológicos, para evaluar la eficacia de las sentencias e incluso para comparar la belleza relativa de las mujeres jóvenes en diferentes regiones en su país. También compartió la fijación de su primo Charles Darwin por la herencia, trató de investigar los cambios de rasgos entre  generaciones. Estaba particularmente interesado en la siguiente pregunta:

Usando las estaturas de sus padres, ¿cómo podemos predecir la altura de una descendencia adulta futura? 

Queremos una línea para predecir la altura de un hijo desde la de sus padres. Queremos una línea que haga de las desviaciones a los datos algo pequeños, y la técnica estándar es elegir una línea ajustada de mínimos cuadrados, para la cual la suma de los cuadrados de los desvíos es la más pequeña. La fórmula para esta línea es sencilla y fue desarrollada por Adrien-Marie Legendre y Carl Friedrich Gauss a finales del siglo XVIII. La línea es generalmente conocida como predicción del mejor ajuste.

En el análisis de regresión básico, la variable dependiente es la cantidad que queremos predecir o explicar, normalmente formando el eje Y vertical de un gráfico, esto a veces se conoce como la variable de respuesta. Mientras que la variable independiente es la cantidad que usamos para hacer la predicción o explicación, generalmente formando el eje X horizontal de un gráfico, y a veces conocida como variable explicativa. El gradiente también se reconoce como coeficiente de regresión. Hay una relación simple entre los gradientes (o tasa de cambio), el coeficiente de correlación de Pearson y las desviaciones estándar de las variables. De hecho si las desviaciones estándar de las variables independientes y dependientes son las mismas, entonces el gradiente es simplemente la correlación del coeficiente de Pearson, que explica su similitud. 

El significado de estos gradientes depende completamente de nuestras suposiciones sobre la relación entre las variables que se están estudiando. Para los datos de correlación, el gradiente indica cuánto esperamos que la variable dependiente cambiará, en promedio, si observamos una diferencia de una unidad para la variable independiente. Por supuesto, que no esperamos que esta predicción coincida con su verdadera diferencia de estaturas de nuestro problema, pero es la mejor conjetura que podemos hacer con los datos disponibles. 

Sin embargo, si asumimos una relación causal, entonces el gradiente tiene una interpretación diferente, es el cambio que esperaríamos en la variable dependiente si interviniéramos y cambiáramos la variable independiente a un valor de una unidad más alta. Los estadísticos son reacios a considerar atribuir causalidad a menos que haya habido un experimento, aunque la informática ha hecho grandes progresos en fijar algunos principios para construir modelos de regresión causal a partir de datos observacionales. 

Las líneas de regresión son modelos que encajan entre un aspecto del mundo que se basa en la simplificación de los supuestos. Esencialmente algún fenómeno estará representado matemáticamente, generalmente incrustado en el software, con el fin de producir una versión simplificada de la realidad, pretendiendo predecir su comportamiento.

Los modelos estadísticos tienen dos componentes principales. En primer lugar, una fórmula matemática que expresa un componente determinista y predecible, por ejemplo, la línea recta ajustada que nos permite hacer predicciones de la altura de un hijo desde la de sus padres. Pero la parte determinista de un modelo no va a ser una representación perfecta del mundo observado. Hay dispersión de alturas alrededor de la línea de regresión, y la diferencia entre lo que el modelo predice, y lo que realmente sucede, es el segundo componente del modelo, y se le conoce como el error residual, aunque es importante recordar que en el modelo estadístico, el “error” no se refiere a un error, sino a la inevitable incapacidad de un modelo para representar exactamente lo que observamos. Así que en resumen, asumimos que:

Observación = modelo determinista + error residual

Esta fórmula se interpreta diciéndonos que, en el mundo estadístico, lo que vemos y medimos a nuestro alrededor, puede ser considerado como una suma de una forma idealizada matemática sistemática, más alguna contribución aleatoria que aún no se puede explicar. Esta es la idea clásica de la señal y el ruido en la instrumentación y las telecomunicaciones. Solo porque actuamos, y algo cambia, no significa que fuimos responsables del resultado. A los seres humanos les resulta difícil de comprender esta simple verdad: siempre estamos dispuestos a construir una narrativa explicativa donde todo está determinado por causas y efectos directos, y sin incertidumbre. Es como interpretar si movemos el interruptor y enciende una lámpara, generalmente nos consideramos responsables de ello. Pero a veces tus acciones claramente no son responsables de un resultado: si no tomamos un paraguas, y llueve, no nos culpamos, aunque puede parecerlo. Pero las consecuencias de muchas de nuestras acciones son menos claras. Supongamos que tiene dolor de cabeza, tome una aspirina y su dolor desaparece. ¿Cómo sabemos que no habría desaparecido aunque no hubieras tomado una tableta? 

Tenemos una fuerte tendencia psicológica a atribuir el cambio a nuestra intervención y esto, provoca el sentido de culpa y sentirnos traicionados. Cadenas de buena o mala suerte no se terminan nunca. Eventualmente las cosas se calman de nuevo, esto también puede ser considerado como regresión media cuadrática, al igual que las estaturas de los hijos dadas por las estaturas de los padres. Pero si creemos que estás en una buen racha, entonces atribuimos por error que es consecuencia normal de nuestras buenas decisiones. Tal vez tiene ramificaciones notables, tales como:

1. Ser despedidos de un trabajo fastidioso y que limita todo nuestro potencial, consideramos en su momento algo malo y triste, para después darnos cuenta de estar en un lugar donde se valora nuestro talento.

2. Al comprar una muy costosa computadora, ir a una universidad de colegiaturas para clases ricas y, al final en la vida profesional darnos cuenta de que ni la tecnología y ni la universidad privada costosa fueron la diferencia, todo cuando vemos triunfar a alguien que tuvo todo adverso pero creyó en la literatura y ser autodidacta. 

La suerte juega un papel considerable en la posición laboral y en el progreso al elegir qué libros estudiar. No significa que el patrón de cambios positivos observado no exista, como tampoco que no haya contribución de error residual. Así que si queremos saber el efecto genuino de ciertas cadenas de causales, entonces debemos seguir el enfoque utilizado para evaluar los modelos determinísticos más su contribución aleatoria del medio^[27]: pronóstico significante.

La regresión lineal múltiple, es tener muchas variables explicativas. Cada variable explicativa es una categoría conceptual operativa que nos da información sobre el objeto observado. Tener relaciones que no son líneas rectas, sino curvas de patrones distintos de datos y variables de respuesta que no son continuas y proporcionales. Esto nos conduce a generalizar la idea de regresión para más de una variable explicativa. No es necesario ajustar la asignación aleatoria para garantizar cada factor distinto del tratamiento principal, debe equilibrarse de todos modos con un solo factor de error de residuo global a todo el grupo de curvas de regresión.

No todos los datos son mediciones continuas, como la estatura de una población. En gran parte del análisis estadístico, las variables dependientes pueden ser las proporciones de eventos que ocurren o no (por ejemplo, la tendencia de personas que sobreviven a COVID-19), el recuento del números de eventos (tal como el cáncer que ocurre en una área agrícola determinada). Cada tipo de variable dependiente tiene su propia forma de regresión múltiple, con una interpretación correspondiente diferente de los coeficientes estimados. Si bien por lo general se instala una línea de regresión lineal a través de los puntos de los datos, la extrapolación ingenua sugiere tratar un gran número de casos, para pronosticar algo más allá al 100%, lo cual es absurdo. Así que se ha desarrollado una forma de regresión para las proporciones, llamada regresión logística, que asegura que una curva no puede ir por encima del 100% o por debajo del 0^[28]%. Este fue un hallazgo controvertido cuando fue publicado en 2001, y ha contribuido a prolongadas disputas sin resolver sobre todo en Inglaterra dentro de la investigación médica. 

Los investigadores han adoptado cuatro estrategias principales de modelización:

1) Representar la matemática lo más simple para justificar las asociaciones, como en los análisis de regresión lineal, que tienden a ser favorecidos para los estadísticos.

2) Modelos deterministas complejos basados en la comprensión científica de un proceso físico, como los utilizados en la predicción del tiempo, que están destinados a representar de manera realista los mecanismos subyacentes y que, generalmente son desarrollados por las matemáticas aplicadas.

3) Algoritmos complejos utilizados para tomar una decisión o predicción que se han derivado de un análisis de un gran número de ejemplos pasados, por ejemplo, para recomendar libros qué le gustaría comprar a un minorista en línea, estos modelos provienen del mundo de la informática conocido como inteligencia artificial. A menudo estas máquinas que aprenden de la experiencia de tratar datos, son cajas negras del cómo se adaptan ellas mismas, pero su estructura interna es algo inescrutable y a la vez rigurosa para considerarla objetivamente.

4) Modelos de regresión que pretenden llegar a conclusiones causales y ratifican con evidencia experimental el medio utilizado de regresión. Estos modelos son ampliamente utilizados por economistas, sociólogos, biólogos, médicos y pedagogos. 

Estas cuatro estrategias desde luego son una gran generalización, afortunadamente las barreras profesionales exitosas están rompiéndose entre disciplinas, y ya estamos siendo testigos de la modelización de la inteligencia artificial, teoría de juegos y otras posturas para tratar el caos del espacio de incertidumbre de nuestra realidad. Pero sea cuales quiera la estrategia adoptada, surge el problema común de construir el modelo, aplicarlo y evaluar su desempeño.

Una buena analogía es que un modelo es como un mapa, en lugar del territorio en sí. Y todos sabemos que algunos mapas son mejores que otros. Uno es muy bueno para conducir en ciudades, pero necesita algo más detallado para caminar en campo abierto. El estadístico británico George Box se ha hecho famoso por su breve pero invaluable aforismo: “todos los modelos están equivocados, algunos son útiles”. Esta afirmación se basó en una vida dedicada a construir experiencia estadística en los procesos industriales, sin duda aprecia el poder de los modelos, pero advierte el peligro de empezar a creer demasiado en ellos como algo que no necesita mejorarse^[29]. 

Pero esta preocupación se olvida fácilmente, una vez que un modelo es aceptado, y especialmente cuando está fuera de las manos de aquellos que lo crearon y entienden sus limitaciones, entonces puede empezar a actuar como una especie de oráculo. En la cotidianidad profesional, perdieron de vista que los modelos son simplificaciones del mundo real, es decir, son los mapas y no el territorio real. El resultado de olvidar esto, son crisis de calidad, accidentes industriales, crisis económicas, fallas en las predicción del clima. 

Pero las ideas básicas de la ciencia estadística todavía se mantienen cuando estamos tratando de resolver problemas prácticos en lugar de científicos. El deseo básico de encontrar la señal de ruido, es de igual relevancia que cuando solo queremos un método que ayude a una decisión particular a la que se enfrenta nuestra vida diaria. El uso de algoritmos, es una fórmula mecanicista que automáticamente producirá una respuesta para cada nuevo caso que viene con una intervención humana adicional, o mínima: esencialmente, esto es tecnología en lugar de ciencia. 

Hay dos tareas generales para un algoritmo de este tipo:

1) Clasificación o también llamado discriminación o aprendizaje supervisado. Se emplea para decir a qué tipo de situación nos enfrentamos, podría utilizarse para separar frutas o semillas por sus características de calidad. 

2) Predicción, se emplea para decirnos lo que va a suceder. Por ejemplo el clima en los próximos días, el precio de algunos productos, el tiempo de remplazo de piezas por desgaste.

Aunque estas tareas difieren en cuanto a si se ocupan del pasado o del futuro, ambas tienen la misma naturaleza subyacente: tomar un conjunto de datos de observaciones pertinentes  a una situación actual y asignarle una conclusión pertinente. Este proceso se ha llamado análisis predictivo, pero estamos abordando el territorio de la inteligencia artificial o IA, en el que algunos algoritmos incorporados en máquinas se utilizan para llevar a cabo tareas que normalmente consumirían cuantiosos recursos humanos en tiempo y número. 

La IA se refiere a sistemas que pueden llevar a cabo tareas muy prescritas. Éxitos de aprendizaje automático que implican el desarrollo de algoritmos de análisis estadístico de grandes conjuntos de datos históricos, se emplean en el reconocimiento de voz, en el navegador de Internet, reconocimiento facial, evaluación de plagio en textos, traducciones de texto, vehículos autónomos, revisión de estilo (https://www.mystilus.com/corrector-de-ortografia) y asistencia de cálculos matemáticos (wolfram alpha). 

Pero una vez más debemos enfatizar que se trata de sistemas tecnológicos que utilizan datos pasados para realizar ajustes que respondan preguntas prácticas inmediatas, en lugar de sistemas científicos que buscan entender cómo funciona el mundo: deben ser juzgados únicamente por el bien que llevan a cabo en sus tareas limitadas en cuestión, aunque la forma de los algoritmos aprendidos por IA pueden proporcionar algunas ideas, no se espera que tengan imaginación o tengan habilidades sobrehumanas en la vida cotidiana. Esto deja a los humanos como los creativos y no profundizaremos más en la IA por estar fuera de nuestro objetivo, es decir, algo más allá de las máquinas de IA.

Desde que Edmund Halley desarrolló fórmulas para calcular seguros y anualidades en la década de 1690, la ciencia estadística se ha preocupado por producir algoritmos para ayudar a la toma de decisiones humanas. El desarrollo de algoritmos en la ciencia de datos continúa esta tradición con el lenguaje R, pero lo ha cambiado para utilizar datos en tiempo real y los llamados Big data. Los conjuntos de datos pueden ser grandes de dos maneras diferentes. En primer lugar, en el número de ejemplos de bases de datos, que pueden ser n objetos, en tono de broma, en nuestros días de bachillerato n solía no ser más grande de unos 100 registros, pero ahora suele haber datos sobre muchos millones o miles de millones de registros. 

La otra forma, es que los datos pueden ser grandes (big) midiendo millones de datos por segundo, hay muchas características científicas e industriales, como ejemplo de ello (https://www.ni.com/es-mx/shop/labview/labview-details.html) la instrumentación virtual industrial y científica. Esta cantidad se conoce a menudo como p, parámetros en tiempo real. En tiempos anteriores unos diez parámetros clínicos definían la salud de una persona, ahora que se comienza a tener acceso al genoma son millones de parámetros posibles, esto ha cambiado radicalmente.

Y ahora que hemos entrado en la era de los grandes n, y grandes problemas con p, cada uno de los problemas puede ser complejo, pensar en los algoritmos que están analizando en muchas publicaciones científicas y de ingeniería, se asemeja a tomar decisiones dentro de millones de registros de publicidad de Facebook y determinar su real impacto. 

Estos son nuevos y emocionantes desafíos que han llevado a oleadas de nuevas personas a la ciencia de datos. Pero, para referirnos al desafío, sin duda que los datos no hablan por sí mismos. Necesitamos procesarlos con cuidados y habilidad si queremos evitar los muchos escollos potenciales de usar algoritmos ingenuamente. Es necesario y fundamental reducir los datos a algo útil. Es decir, encontrar patrones. 

Una estrategia para tratar con números excesivos de registros es identificar grupos que son similares, un proceso conocido como Clustering o aprendizaje no supervisado, ya que tenemos que aprender acerca de estos grupos sobre algo que de antemano no sabemos. Un modelo de este tipo es la Law Benford’s por ejemplo, permite saber si los datos fueron generados de forma natural o fueron alterados para engañar de manera deliberada.  Encontrar clústeres bastantes homogéneos puede ser un fin en sí mismo, caracterizar versiones similares, dar etiquetas de categoría, hace necesario  algoritmos para clasificar estos casos. Una vez identificados los clústeres pueden entonces ser alimentados de nuevos datos y el algoritmo construye dentro de estas categorías. 

Antes de seguir construyendo un algoritmo para la clasificación o predicción, es posible que también tengamos que reducir los datos sin procesar a dimensiones manejables debido a un p excesivamente grande, es decir, demasiadas características que se miden en cada caso. Este proceso se conoce como ingeniería de características o identificación de conceptos operativos en la ciencia. Solo considere el número de medidas que podrían hacerse en un rostro humano, que pueden necesitar ser reducidas a un número limitado de parámetros importante, que el software pueda utilizar para realizar el reconocimiento facial y compararlo con registros en una base de datos. Las medidas que carecen de valor para la predicción o la clasificación se pueden identificar mediante métodos de visualización o regresión de datos y, a continuación descartar cantidades importantes de datos formando medidas compuestas (parámetros) que encapsulan la mayor parte de la información.

En algunos desarrollos con gran poder de cómputo, como el etiquetado de categorías, sugiere que esta etapa inicial de reducción de datos puede no ser necesaria y los datos totales sin procesar se pueden tratar en un solo algoritmo.

Clasificación y predicción. Un rango desconcertante de métodos alternativos ahora está disponible para crear algoritmos de clasificación y predicción. Los investigadores solían promover métodos que provenían de sus propios orígenes disciplinares (profesión), por ejemplo, los estadísticos prefieren modelos de regresión, mientras que los informáticos prefieren la lógica basada en reglas o también llamadas redes neuronales que son formas alternativas de tratar de imitar la cognición humana.

La implementación de cualquiera de estos métodos nos demanda habilidades especiales y software, pero ahora los programas de estadística, permiten una selección de la técnica como un menú y así se fomenta más un enfoque donde el rendimiento de interpretación es más importante que la filosofía de modelación interior de redes neuronales.

En cuanto el rendimiento práctico de los algoritmos comenzó a ser medido y comparado, la persona inevitablemente se volvió competitiva y ahora hay hasta concursos científicos de la ciencia de datos organizados por la plataforma Kaggle.com. Organizaciones comerciales y académicas proporcionan un conjunto de datos para que los interesados los descarguen: los desafíos han incluido la detección de ballenas a partir de grabaciones sonoras, la contabilidad de la materia oscura en datos astronómicos y la predicción de ingresos a hospitales. En cada caso, a los interesados se les proporciona un conjunto de datos de entrenamiento sobre el que crea sus algoritmos y un conjunto de pruebas que decidirá su rendimiento. Para el análisis, es crucial dividir los datos en un conjunto de entrenamiento utilizado para crear el algoritmo, y un conjunto de pruebas que se mantienen esperadas y solo se utilizan para evaluar el rendimiento, sería un grupo serio mirar el conjunto de pruebas antes de que estemos listos con un algoritmo completo. 

1.6 ¿Por qué necesitamos la teoría de la probabilidad al hacer estadísticas? 

Ya hemos visto que el concepto de datos, es algo que se “eligen al azar” de una distribución de la población. Tenemos que asumir que cualquier elemento de la población es igualmente probable que sea elegido para ser parte de nuestra muestra. Y si queremos hacer inferencias estadísticas sobre aspectos desconocidos del mundo, incluyendo hacer predicciones o pronósticos, entonces nuestras conclusiones siempre tendrán cierta incertidumbre asociada a los datos. 

Ya hemos considerado dar cuenta, observar cuánta variación esperaríamos que tuviéramos nuestra muestra en el resumen estadístico si repetimos el proceso de muestreo una y otra vez, y luego usamos esta variabilidad para expresar nuestra incertidumbre sobre las características verdaderas, pero desconocidas, de la población. Esto de nuevo solo necesita la idea de “elegir al azar”, una idea que incluso los niños pequeños pueden entender fácilmente como una elección justa. 

Tradicionalmente, un curso de estadística comenzará con probabilidad, pero está iniciación matemática puede entorpecer la idea de que no es necesaria la teoría de la probabilidad. Así que a la inferencia estadística la llegaremos más tarde. Pero es ahora momento de enfrentar su papel vital en proporcionar “el leguaje de la incertidumbre”. Los estudiantes consideran difícil e inadecuado iniciar el estudio de la probabilidad por ser compleja y poco intuitiva. 

La idea más intuitiva como punto de partida de la probabilidad, quizá es la “frecuencia esperada”. Cuando nos enfrentamos al problema de dos monedas, nos preguntamos ¿Qué esperaría que pasara si probara el experimento varias veces? Digamos que intentamos voltear primero una moneda y luego la otra, un total de cuatro veces. Sospechamos que con un poco de pensamiento, podemos concluir que esperaríamos obtener los resultados mostrados:

Así que 1 de cada 4 veces esperaríamos tener dos caras. Por lo tanto, dice el razonamiento que la probabilidad de que en un intento en particular usted obtenga dos caras es 1 en 4, o 1/4. Lo cual, afortunadamente es correcto. Este árbol de frecuencia esperado puede transformarse en un árbol de probabilidad etiquetando cada división con fracción de ocasiones que se toma. 

Es claro entonces que tener la probabilidad general de toda una rama del árbol, por ejemplo, una cara seguida de una cara, se obtiene multiplicando las fracciones en las divisiones a lo largo de la rama, de modo que: 1/2 x 1/2=1/4.

Los árboles de probabilidad son una forma de generalizar y extremadamente efectiva de enseñar la probabilidad. De hecho, podemos utilizar este sencillo ejemplo de voltear dos monedas para ver todas las reglas de probabilidad, ya que estas reglas muestran que:

1. La probabilidad de un evento es un número entre 0 y 1, para eventos imposibles cero y, uno para eventos con el 100% de certeza.

2. Regla de complemento: la probabilidad de que ocurra un evento, es 1 menos la probabilidad de que no ocurra. Por ejemplo, la probabilidad de “al menos una cara”, es 1 menos la probabilidad de dos caras: 1-1/4=3/4.

3. La adición, o regla de OR: agregue probabilidad de eventos mutuamente excluyentes (lo que significa que ambos no pueden ocurrir al mismo tiempo) para obtener la probabilidad total. Por ejemplo, la probabilidad de “al menos una cara” es de 3/4, ya que comprende “dos caras” o “cara + cruz” o “cruz + cara”, cada una con probabilidad de 1/4.

4. La multiplicación, la regla de AND: multiplicar probabilidades de que ocurra una secuencia de eventos independientes (lo que significa que uno no afecta al otro). Por ejemplo, la probabilidad de una cara y una cara, es 1/2 x 1/2= 1/4.

Todavía estamos haciendo suposiciones fuertes, incluso en este sencillo ejemplo de volteo de monedas. Estamos asumiendo que la moneda es justa y equilibrada; se voltea correctamente para que el resultado no sea predecible; no aterriza en su borde;  COVID-19 no nos mata después de la primera voltereta, y así sucesivamente. Estas son consideraciones serias (excepto posiblemente el ¡COVID-19!). Sirven para enfatizar que todas las probabilidades que usamos están condicionadas, no existen tal cosa como probabilidad incondicional de un evento; siempre hacemos suposiciones y otros factores que podrían afectar la probabilidad. Y, como vemos ahora, tenemos que tener cuidado con lo que condicionamos. 

La probabilidad condicional: cuando nuestras probabilidades dependen de otros eventos. En el caso dos monedas, los eventos eran independientes, ya que la probabilidad de voltear una cara en un momento no dependía de cuál fue la primera levantada. En la escuela normalmente aprendemos sobre eventos dependientes al hacer preguntas un tanto tediosas sobre, por ejemplo, una serie de extracciones de bolas de un cajón. El ejemplo anterior es algo más relevante para la vida real. 

Este tipo de problema es clásico en pruebas de inteligencia y no es un problema fácil de resolver, pero usando la idea de la frecuencia esperada se vuelve notablemente sencillo. La idea crucial es pensar lo que esperaríamos que pasará a un grupo de cosas. Es fácil confundir la probabilidad de una prueba positiva, con la probabilidad de acertar dada una prueba positiva. Este tipo de confusión se conoce como la falacia del fiscal, ya que es tan frecuente en los casos judiciales relacionados, por ejemplo, con imputaciones por ADN, un experto forense podría afirmar, por ejemplo, que si el acusado es inocente, solo hay uno de cada mil millones de posibilidades de que coincida con el ADN encontrado en la escena del crimen. Pero esto se interpreta erróneamente como un significado “dadas pruebas de ADN”, solo hay 1 en mil millones de posibilidades de que el acusado sea inocente. 

Es un error fácil de cometer, porque esta la lógica es tan defectuosa como pensar la declaración “si eres el Profesor, entonces eres escritor”, donde el defecto es algo más simple de detectar. 

1.6.1 ¿Qué es probabilidad de todos modos? 

Tenemos la idea que probabilidad es algo que asignamos números, una cantidad “virtual”, en la que podemos poner un número a la posibilidad de un evento, pero nunca podemos medir directamente. Aún más preocupante es hacer la pregunta bastante obvia: ¿qué significa probabilidad de todos modos? Esto puede parecer pedante, pero la filosófica de la probabilidad es a la vez un tema apasionante en sí mismo y también tiene un papel importante en las aplicaciones prácticas de las estadísticas. 

No espere un consenso ordenado de los expertos. Pueden estar de acuerdo en las matemáticas de la probabilidad, pero los filósofos y estadísticos han ideado todo tipo de ideas diferentes para lo que estos números escurridizos realmente significan, y discutir intensamente sobre ellos genera corriente de pensamiento radicales. Algunas sugerencias populares son:

Probabilidad clásica. Esto es lo que se enseña en la escuela, basado en las simetrías de monedas, dados, cartas…, y se puede definir como: la relación de números de resultados que favorecen el evento, dividido por el número total de posibles resultados, suponiendo que los resultados sean igualmente probables.

Probabilidad enumerativa. Supongamos que hay tres bolas blancas y cuatro negras en un cajón, y tomamos una bola al azar, ¿cuál es la probabilidad de sacar una bola blanca? Es 3/7, obteniendo enumerando las oportunidades. Muchos hemos tenido que sufrir con preguntas de estas, pero es solo una extensión de la probabilidad clásica que requiere la idea de una elección aleatoria de un conjunto físico de objetos. Hemos estado utilizando esta idea extensamente ya que al describir un puntual conjunto de datos (muestra) se elogia el azar de una población. 

Probabilidad de frecuencia Long-run. Esto se basa en la proporción de veces que ocurre un evento en una secuencia infinita de experimentos idénticos. Esto puede ser razonable (al menos teóricamente) para eventos infinitamente reptiles, pero ¿Qué pasa en ocasiones únicas como las carreras de galgos, o el clima del día de mañana? De hecho, casi cualquier situación realista no es, ni siquiera en principio, infinitamente repetible.

Propensión o casualidad. Esta idea de que hay algunas cosas tendenciosas objetivas de la situación a producir un evento: causa - efecto. Esto es superficialmente atractivo: si fuera un ser omnisciente, tal vez podrías decir que había una probabilidad particular de que su taxi llegara pronto, o de ser atropellado por un elefante el día de hoy. Pero parece no proporcionar ninguna base para que los mortales estimen esta “verdadera oportunidad o tragedia” metafísica. 

Probabilidad subjetiva o personal. Este es el juicio de una persona específica sobre una ocasión específica, basada en sus conocimientos presentes, se interpreta más o menos en términos de las cuotas de apuesta que encontrarían información razonable para su sustento. Es el caso de la investigación experimental biológica.

Desde luego que diferentes expertos tienen su propia preferencia entre estas alternativas, pero como investigador científico preferimos la última: la probabilidad subjetiva. Esto significa que tomamos la opinión de que cualquier probabilidad numérica se construye esencialmente de acuerdo con lo que se conoce en el estado del arte del conocimiento (revisión de literatura) y el diseño experimental empírico bayesiano. Este enfoque constituye la base de la escuela bayesiana de inferencia estadística que es el rasgo distintivo moderno de las ciencias naturales.

Pero afortunadamente no tienes que estar de acuerdo con nuestra posición, de que las probabilidades numéricas no existen objetivamente. Es bueno suponer que las monedas y otros dispositivos aleatorizantes son objetivamente aleatorios, en el sentido de que dan lugar a datos tan impredecibles que son indistinguibles de aquellos que esperaríamos que surjan de probabilidades “objetivas”. Así que generalmente actuamos como si las observaciones son aleatorias, incluso cuando sabemos que esto no es estrictamente cierto. Los ejemplos más extremos de esto son generadores de números pseudoaleatorios informáticos, que de hecho se basan en cálculos lógicos y completamente predecibles. No contienen aleatoriedad alguna, pero su mecanismo es tan complejo que en la práctica son indistinguibles a partir de secuencias verdaderamente aleatorias, digamos, las obtenidas de una fuente de partículas subatómicas.  

Esta extraña habilidad para actuar como si algo fuera verdad, cuando sabes que realmente no lo es, por lo general se consideraría peligrosamente irracional. Sin embargo, será útil cuando se trata de utilizar la probabilidad como base para el análisis estadístico de los datos y el diseño experimental. Pero afortunada mente la segunda ley de la termodinámica, el movimiento molecular browniano, el genotipo…, nos ayudan con la aleatorización de poblaciones.  

Ahora llegamos a la etapa crucial pero difícil de establecer la conexión general entre la teoría de la probabilidad, los datos y aprender sobre cualquier población objetivo que nos interese científicamente. La teoría de la probabilidad entra naturalmente en juego en lo que llamaremos situación 1:

1. Cuando la muestra de datos puede considerarse generada por algún dispositivo aleatorizante, por ejemplo, al lanzar dados, voltear monedas o asignar aleatoriamente a un individuo a un tratamiento médico utilizando un generador de números azarosos y luego registrar los resultados de sus tratamiento. 

Pero en la práctica podemos enfrentarnos a la situación 2:

2. Cuando un dispositivo de aleatorización elige una muestra preexistente, digamos al seleccionar a las personas para que participen en una encuesta. 

Y la mayor parte del tiempo nuestros datos surgen de la situación 3:

3. Cuando no hay aleatoriedad en absoluto deliberada introducida por el observador, pero actuamos como si el punto de datos (muestra) fuera generado de hecho por algún proceso aleatorio, por ejemplo, en la interpretación del peso al nacer del bebé de un conocido. 

La mayoría de las exposiciones no dejan claro estas distinciones: la probabilidad generalmente se enseña utilizando dispositivos aleatorizantes (1) y las estadísticas se enseñan a través de la idea de “muestreo aleatorio” (2), pero de hecho la mayoría de las aplicaciones de estadística científicas no implican ningún dispositivo aleatorio o muestreo de ningún tipo (situación 3), como si se tratara de habitar en un mundo con la segunda ley de la termodinámica.

Pero primero consideremos las situaciones 1 y 2. Justo antes de operar el dispositivo aleatorizante, suponemos que tenemos un conjunto de posibles resultados que podrían observarse, junto con sus respectivas probabilidades, por ejemplo, una moneda puede ser cara o cruz, cada una con 1/2 de probabilidad. Si asociamos cada uno de estos posibles resultados decimos que tenemos una variable aleatoria con una distribución de probabilidad. En la situación 1, el dispositivo aleatorizante asegura que la observación se genera al azar a partir de esta distribución, y cuando se observa, la aleatoriedad se ha ido y todos estos futuros potenciales se han desplomado hasta observaciones reales. Del mismo modo, en la situación 2, si medimos a un individuo al azar, por ejemplo, sus ingresos, entonces esencialmente hemos extraído una observación al azar de una distribución poblacional de los ingresos. 

Así que la probabilidad es claramente relevante cuando tenemos un dispositivo aleatorizante. Pero la mayoría de las veces simplemente consideramos todas las mediciones disponibles para nosotros en ese momento, que pueden haber sido recogidas informalmente, o, como vimos, incluso representan todas las observaciones posibles: piense en las tasas de supervivencia para la cirugía cardíaca infantil en diferentes hospitales o todos los resultados del examen para los niños mexicanos, ambos comprenden todos los datos disponibles, y no habido muestreo aleatorio.

Hemos discutido la idea de una población metafórica, que comprende las posibilidades que podrían haber ocurrido, pero principalmente no pasaron, como la idea de disponer d aun medio para hacernos de más datos a partir de empíricos observados, crear de manera sintética un universo mayor de datos siguiendo el patrón de los primeros, ya al agregar más datos empíricos ajustar el modelo. Ahora tenemos que prepararnos para un paso aparentemente irracional: tenemos que actuar como si los datos fueran generados por un mecanismo aleatorio de esta población, aunque sobemos muy bien que no lo fue.

Si observamos toda la población, ¿dónde entra la probabilidad?

Cuando los eventos extremos ocurren en estrecha sucesión, como múltiples accidentes de bicicleta y correlación con desastres naturales, hay una proposición natural a sentir que está en cierto sentido vinculada. A continuación, se vuelve importante averiguar cuán inusuales son estos eventos. Por ejemplo, evaluar ¿cuán raro es un grupo de menos de siete homicidios en un día en la ciudad? Si podemos construir una distribución de probabilidad razonable para el número de homicidios por día, entonces podemos responder a la pregunta planteada. 

Pero, ¿cuál es la justificación para construir una distribución de probabilidad? El número de homicidios registrados cada día en la ciudad es simplemente un hecho: no ha habido muestreo y no hay ningún elemento aleatorio explícito que genere cada evento desafortunado. En un mundo inmensamente complejo e impredecible, cualquiera que sea nuestra filosofía personal detrás de la suerte o la fortuna, resulta que es útil actuar como si estos eventos fueran producidos por algún proceso aleatorio impulsado por la probabilidad.

Podría ser útil imaginar que al principio de cada día tenemos una gran población de personas, cada una de la cuales tiene una posibilidad muy pequeña de ser víctima de homicidio. Datos de este tipo pueden representarse como observaciones de una distribución de Poisson, que fue desarrollada originalmente por Siméon Poisson en Francia en 1830 para representar el patrón de condenas injustas por año. Desde entonces se ha utilizado para modelar todo, desde el número de goles marcados por un equipo de fútbol en un partido o el número de boletos de lotería ganadores en cada semana. En cada una de estas situaciones hay un gran número de oportunidades para que ocurra un evento, pero cada uno con una probabilidad muy baja de ocurrencia, y esto da lugar a la distribución extraordinariamente versátil de Poisson.

Mientras que la distribución normal (o gaussiana) requiere dos parámetros —la media de la población y la desviación estándar—, la distribución de Poisson depende únicamente de su media. Sin embargo debemos comprobar si Poisson es una suposición razonable, de modo que sea razonable actuar como si el número que describe  fuera una observación aleatoria extraída de una distribución de Poisson con una media definida. El ajuste de esta distribución de probabilidad matemática a los datos empíricos, es casi inquietantemente buena. A pesar de que hay una historia única detrás de cada uno de estos trágicos acontecimientos de homicidio, la mayoría de los cuales son impredecibles, los datos actúan como si realmente fueran generados por algún mecanismo aleatorio conocido. Una posible opinión es pensar que otras personas podrían haber sido asesinadas, pero no lo fueron, hemos observado uno de los muchos mundos posibles que podrían haber ocurrido, al igual que cuando volteamos monedas observamos una de las muchas secuencias posibles. 

Adolphe Quetelet fue astrónomo, estadístico y sociólogo en Bélgica a mediados de la década de 1800, fue uno de los primeros en llamar la atención sobre la asombrosa previsibilidad de los patrones generales formados por eventos individualmente impredecibles. Es intrigante la aparición de distribuciones normales en fenómenos naturales, como la distribución del peso al nacer que acuñó la idea de asumir el valor medio de todas estas características. Así se desarrolló la idea de la “física social”, ya que la regularidad de las estadísticas sociales parecía reflejar un proceso subyacente casi mecanicista. Así como las moléculas aleatorias de un gas se unen para hacer propiedades físicas predecibles, el funcionamiento impredecible de millones de vidas individuales se unen para producir, por ejemplo, tasas nacionales de suicidios que apenas cambian de un año a otro.

Afortunadamente no tenemos que creer que los eventos son realmente impulsados por la aleatoriedad pura (sea lo que sea).  Es simplemente que una suposición de “azar” encapsula toda la imprevisibilidad inevitable en el mundo, o lo que a veces se denomina variabilidad natural. Por lo tanto, hemos establecido que la probabilidad constituye la base matemática adecuada tanto para la aleatoriedad “pura”, que ocurre con partículas subatómicas, monedas, dados…, y variabilidad “natural”, inevitable, como en los pesos al nacer, supervivencia de una cirugía, resultados de un examen, homicidios y cualquier otro fenómeno que no sea totalmente predecible.

1.6.2 Juntas probabilidad y estadística

Ya hemos discutido la idea de variable aleatoria: un único punto de datos extraído de una distribución de probabilidad descrita por los parámetros. Paro rara vez nos interesa un solo punto de datos: generalmente tenemos una masa de datos que resumimos en determinados promedios, medianas y otras estadísticas. El paso fundamental que daremos es considerar esas estadísticas como variables aleatorias, extraídas de sus propias distribuciones. 

Esto es un gran avance, y uno que no solo ha desafiado a generaciones de estudiantes de estadística, sino también a generaciones de estadísticos que han tratado de averiguar de qué distribuciones debemos asumir estas estadísticas. Es razonable preguntarnos por qué necesitamos todas estas matemáticas, cuándo podemos resolver intervalos de incertidumbre y así sucesivamente el uso de enfoques de arranque basados en la simulación. 

Pero estas simulaciones son torpes y consumen mucho tiempo, especialmente con grandes conjuntos de datos, y en circunstancias más complejas no es sencillo averiguar lo que se debe simular. Por el contrario, las fórmulas derivadas de la teoría de la probabilidad proporcionan perspicacia, conveniencia, y siempre conducen a la misma respuesta, ya que no dependen de una simulación en particular. Pero otra cara de la moneda es que esta teoría se basa en suposiciones, y debemos tener cuidado de no ser engañados por la impresionante álgebra para aceptar conclusiones injustificadas. Exploraremos esto con más de talle, pero primero, habiendo apreciado ya el valor de las distribuciones normal y Poisson, necesitamos introducirnos a otra distribución de probabilidad importante. 

Supongamos que extraemos muestras de diferentes tamaños de una población que contiene exactamente 20% de bolas negras y 80% de bolas blancas, y calculamos la probabilidad de observar diferentes proporciones posibles de negras. Por supuesto, este es el camino equivocado —queremos usar la muestra conocida para aprender acerca de la población desconocida— pero solo podemos llegar a esta conclusión explorando primero cómo una población conocida da lugar a diferentes muestras.

El caso más simple es una muestra de tamaño uno, cuando la proporción observada debe ser 0 o 1 dependiendo  de si seleccionamos una bola blanca o negra, y estos eventos ocurren con una probabilidad de 0.8 y 0.2 respectivamente. La distribución resultante se muestra:

Si tomamos dos bolas al azar, entonces las proporciones de negras serán 0 (ambas blancas), 0.5 (una de cada una) o 1 (ambas negras). Estos eventos se producirán con probabilidades 0.64, 0.32 y 0.04 respectivamente. Y esta distribución de probabilidad se muestra el gráfico de arriba. Del mismo modo, podemos utilizar la teoría de probabilidades para calcular la distribución de probabilidad para las proporciones observadas de bolas negras y blancas en 5, 10, 100 y 1000 extracciones (se muestra en el gráfico). Estas distribuciones se basan en lo que se conoce como la distribución binomial y también pueden decirnos la probabilidad, por ejemplo, de conseguir al menos un 30% de bolas negras en 100 extracciones, conocida como zona de cola. 

La media de una variable aleatoria también se conoce como su expectativa, y en todas estas muestras esperamos una proporción de 0.2 o 20%: todas las distribuciones mostradas en el gráfico tienen 0.2 como su media. La desviación estándar para cada una se da mediante una fórmula que depende de la proporción subyacente, en este caso 0.2 y el tamaño de la muestra. Tenga en cuenta que la desviación estándar de una estadística se denomina generalmente el error estándar, para distinguirlo de la desviación estándar de la distribución de la población que la deriva. Esta figura tiene algunas características distintivas. En primer lugar, las distribuciones de probabilidad tienden a una forma regular, simétrica y normal a medida que aumenta el tamaño de la muestra, tal como observamos mediante simulaciones de arranque. En segundo lugar, las distribuciones se estrechan a medida que aumenta el tamaño de la muestra. En el siguiente paso, debemos mostrar cómo se puede utilizar una simple aplicación de estas ideas para identificar rápidamente si una declaración estadística es razonable o no. Incluso en una era de datos abiertos, ciencias de datos y periodismo de datos, todavía necesitamos principios estadísticos para no ser engañados por patrones aparentes en los números. 

1.6.3 El teorema del límite central

“El teorema del límite central o teorema central del límite indica que, en condiciones muy generales, si es la suma de n variables aleatorias independientes, con media conocida y varianza no nula pero finita, entonces la función de distribución de «se aproxima bien» a una distribución normal (también llamada distribución gaussiana, curva de Gauss o campana de Gauss). Así pues, el teorema asegura que esto ocurre cuando la suma de estas variables aleatorias e independientes es lo suficientemente grande^[30]”.

Los puntos de datos individuales del teorema del límite central podrían extraerse de una amplia variedad de distribuciones de poblacionales, algunas de las cuales podrían estar sesgadas, con colas largas como las de los ingresos monetarios o parejas sexuales. Pero ahora hemos hecho el cambio crucial para considerar distribuciones estadísticas en lugar de puntos de datos individuales y, estas estadísticas serán comúnmente promedios de algún tipo. Ya hemos visto que las distribuciones de las medias de la muestra de los remuestreos de arranque tiende a una forma simétrica bien comportada, sea cualquiera la forma de la distribución original de los datos, y ahora podemos ir más allá de esto a una idea más profunda y bastante notable, establecida hace unos 300 años.

El ejemplo de las bolas negras muestra que la variabilidad en proporción observada se hace menor a medida que aumenta el tamaño de la muestra, es por eso que los datos se estrechan alrededor de la media. Esta es la clásica Ley de Grandes Números, que fue establecida por el matemático suizo Jacob Bernoulli a principios del siglo XVIII: una sola moneda, asumiendo el valor 1 si es cara y 0 si es cruz, se dice que es un ensayo bernoulli y tiene una distribución Bernoulli. Si seguimos volteando la moneda equilibrada (justa), llevando a cabo cada vez más ensayos de Bernoulli, entonces la proporción de cada resultado se acercará cada ves más al 50% de caras y cruces, decimos que la proporción observada converge en la verdadera posibilidad subyacente de una cara. Por supuesto, al principio de la secuencia de relación puede ser de alguna manera a partir de 50:50, digamos después de una serie de volteretas de la moneda, y la tentación es creer que las cruces de alguna manera ahora “se deben” para que la población se equilibre, esto se conoce como la falacia del “jugador” y es un sesgo cognitivo que expresa la persona, bastante difícil de superar. Pero la moneda no tiene memoria, la idea clave es que la moneda no puede compensar los desequilibrios del pasado, sino simplemente abrumarlos cada vez con más nuevos levantamientos independientes. 

La campana de distribución normal o gaussiana, argumentamos que es el resultado: depende de un gran número de factores, todos los cuales tienen un poco de influencia, cuando sumamos las contribuciones de todos los efectos obtenemos de un experimento una distribución normal. Esto es el razonamiento detrás de lo que se conoce como el teorema límite central, demostrado por primera vez en 1733 por el matemático francés Abraham de Moivre para el caso particular de la distribución binomial. Pero no es solo la distribución binomial la que tiende a una curva normal con un tamaño de muestra creciente, es un hecho notable que prácticamente cualquiera que sea la forma de la distribución de la población que se muestra, cada una de las mediciones originales, para grandes tamaños de muestra su promedio puede considerarse extraído de una curva normal. Esto tendrá una media que es igual a la media de la distribución original y una desviación estándar que tiene una simple desviación relacional con la desviación estándar de la distribución de la población original y, como ya se ha mencionado, a menudo se conoce como el error estándar.

Aparte de su trabajo sobre conocimiento de poblaciones, la correlación, la regresión y casi todo lo demás, Francis Galton también consideró un verdadera maravilla la distribución normal, entonces conocida como la ley de frecuencia de error, sugiere que dentro del caos saldrá algo de una manera ordenada. 

¿Cómo nos ayuda esta teoría a averiguar la exactitud de nuestras estimaciones? Toda teoría está bien prueba cosas sobre distribuciones estadísticas basadas en datos extraídos de poblaciones conocidas, pero eso no es lo que nos interesa principalmente. Tenemos que encontrar una manera de revertir el proceso: en lugar de pasar de poblaciones conocidas a decir algo sobre las posibles muestras, tenemos que pasar de una sola muestra a decir algo sobre una posible población. Este es el proceso de inferencia inductiva esbozado aquí. 

Levantar una moneda y creer que la relación es 50:50, este sencillo ejercicio revela una distinción importante entre dos tipos de incertidumbre: lo que se conoce como incertidumbre aleatoria, se da antes de voltear la moneda —la oportunidad de un evento impredecible— y la incertidumbre epistémica después de dar la vuelta a la moneda, una expresión de nuestra ignorancia personal sobre un evento fijo pero desconocido. La misma diferencia existe entre un boleto de lotería (donde el resultado depende del azar) y una tarjeta de rascar (el resultado ya está decidido, pero no sabes lo que es). 

Las estadísticas se utilizan cuando tenemos incertidumbre epistémica sobre alguna cantidad del mundo. Por ejemplo, realizamos una encuesta cuando no sabemos la verdadera proporción en una población que se considera afín a una ideología, o realizamos un ensayo de fertilizantes cuando no sabemos el verdadero promedio de un porción de fertilizante en un vegetal particular. Como hemos visto, estas cantidades fijas pero desconocidas se llaman parámetros y a menudo se les da una letra griega. Al igual que el cambio de moneda, antes de hacer estos experimentos tenemos una incertidumbre aleatoria sobre cuáles pueden ser los resultados, debido al muestreo aleatorio o la asignación aleatoria de plantas a fertilizar. Luego, después de haber hecho el estudio y obtener los datos, usamos este modelo de probabilidad para controlar nuestra incertidumbre epistémica actual, al mismo tiempo que finalmente estamos preparado para decir “50:50” sobre la moneda cubierta. Así que la teoría de la probabilidad que nos dice qué esperar en el futuro, se utiliza para decirnos lo que podemos aprender de lo que hemos observado en el pasado. Esta es la base para la inferencia estadística (bastante notable).

El procedimiento para derivar un intervalo de incertidumbre alrededor de nuestra estimación, o equivalentemente un margen de error, se basa en esta idea fundamental  de cuatro etapas: 

1. Utilizamos la teoría de probabilidad para decirnos, para cualquier parámetro de población en particular, un intervalo en el que esperamos que la estadística observada se encuentre con un 95% de probabilidad. Estos son intervalos de predicción del 95%.

2. Luego observamos una estadística en particular.

3. Por último (y esta es la aparte difícil) calcular el rango de posibles parámetros de población para los que nuestra estadística se encuentra en sus intervalos de confianza del 95%.

4. Este intervalo de confianza resultante recibe la etiqueta de “95%” ya que, con la aplicación repetida, el 95% en estos intervalos debe asegurar contener el valor verdadero. 

Un intervalo de confianza es el rango de parámetros de población para los que nuestra estadística observada es una consecuencia plausible. Es necesario conocer como es su cálculo, pero por ahora continuaremos con nuestra discusión global.

El principio de intervalo de confianza fue formalizado en la década de 1930 en la Universidad College de Londres por Jerzy Neyman, un brillante matemático y estadístico polaco y Egon Pearson, hijo de Karl Pearson. El trabajo se derivo las distribuciones de probabilidad necesarias para coeficientes de correlación estimados y coeficientes de regresión que había estado ya aplicándose durante décadas antes, y en cursos de estadísticas académicas estándar se proporciona los detalles matemáticos de estas distribuciones, e incluso derivados de los primeros principios. Afortunadamente, los resultados de todos estos trabajos están ahora encapsulados en software estadístico de R, por lo que los profesores pueden centrarse en las cuestiones esenciales y no distraerse con fórmulas complejas. 

En resumen, la teoría de probabilidad se puede utilizar para derivar la distribución de muestreo de estadísticas resumidas, de las cuales se pueden derivar fórmulas para parámetros de confianza. Un intervalo de confianza del 95% es el resultado de un procedimiento que, en el 95% de los casos en los que sus suposiciones son correctas, contendrá el valor verdadero. El teorema del límite central implica que se puede suponer que las medias de muestra y otras estadísticas de resumen tienen una distribución normal para muestras grandes. Los márgenes de error generalmente no incorporan errores sistemáticos debido a causas no aleatorias: se requiere conocimiento externo y juicio para evaluarlos. Los intervalos de confianza se pueden calcular incluso cuando observamos todos los datos, que luego representan incertidumbres sobre los parámetros de una población metafórica subyacente. 

Hemos llegado quizás a la parte más importante del ciclo de resolución de problemas, en el que buscamos respuestas a preguntas específicas sobre cómo funciona el mundo. Por ejemplo:

¿Existe el bosón de Higgs?

¿Tomar estatinas reduce el riesgo de ataques cardíacos y accidentes cerebrovasculares en personas adultas?

Se pueden hacer hacer preguntas del tipo transitorio hasta lo eterno:

Boson de Higgs: podría cambiar las ideas básicas de las leyes físicas del universo.

Estatinas: es una declaración científica, pero específica para un grupo. 

Si tenemos datos que pueden ayudarnos a responder a algunas de estas preguntas, con los que ya hemos hecho algún ensayo exploratorio y hemos sacado algunas conclusiones informales sobre un modelo estadísticos adecuado. Ahora llegamos a un paso formal de la parte de análisis del ciclo PPDAC, generalmente conocido como pruebas de hipótesis. Modelo PPDAC (Problema, Plan, Datos, Análisis, Conclusiones) de MacKay y Oldford (1994^[31]).

1.6.4 Hipótesis estadística 

¿Qué es una hipótesis? Uno puede definirla como una explicación propuesta para un fenómeno en términos de comparación, relación o causal: una proposición factual solo admite dos estados, falsa o verdadera, donde el criterio sobre su verdad es ontológico (empírico). La hipótesis no es una verdad absoluta, sino una suposición provisional y de trabajo de investigación, tal vez es mejor considerarla una sospecha de nuestra mente causal sobre lo real, un potencial de conocimiento e información. Esto expresa la idea de modelo estadístico como una representaciones matemáticas de observaciones conscientes, estructuras con fundamentos (componentes deterministas) y componentes estocásticos (variables de aleatorización natural o sintéticas). La incertidumbre o imprevisibilidad y el error, generalmente son expresados en términos de distribución de probabilidad. Dentro de la ciencia de datos, se considera que una hipótesis es una suposición particular sobre uno de estos componentes de un modelo estadístico, en lugar de la verdad absoluta, se presenta como una verdad graduada entre cero y uno. 

No solo son los científicos los que valoran descubrir conocimiento dentro de la nube de incertidumbre con que se nos presenta la realidad. De hecho, es deseable que nuestro cerebro tenga una tendencia innata a ver patrones donde no existen, y esta tendencia podría incluso explicar una ventaja evolutiva para ajustar hipótesis con nuevos datos y así sobrevivir. Debe haber una manera de protegernos de falsas ideas, los primeros intentos de probar hipótesis fue ese papel. 

La idea de una hipótesis nula se mueve ahora central: es la forma simplificada de modelo estadístico con la que vamos a trabajar hasta que tengamos suficiente evidencia en su contra. La hipótesis nula es lo que estamos dispuestos a asumir en el caso hasta que se demuestre lo contrario, es la hipótesis contraria a la que sugiere nuestra reflexión de conocimiento previo. Es implacablemente negativa, negando todo progreso y cambio. Pero esto no significa que realmente creamos que la hipótesis nula es literalmente cierta: debe quedar claro que ninguna de las hipótesis nulas es plausible. Así que nunca podemos afirmar que la hipótesis nula ha sido realmente probada: en palabras de otro gran estadístico británico Ronald Fisher: “la hipótesis nula nunca se prueba ni se establece, pero es posible refutarla, en el discurso de la experimentación. Se puede decir que cada experimento existe solo para dar a los hechos la posibilidad de refutar la hipótesis nula^[32]”. Por ejemplo:

Hipótesis 1: el salario promedio en Michoacán es diferente al salario promedio de Guanajuato

H1: Salario promedio de Michoacán 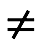salario promedio de Guanajuato 

La hipotesis nula Ho sería: 

Ho: Salario promedio de Michoacán = salario promedio de Guanajuato 

El valor p nos indicará cuál de las dos hipótesis es con la que nos quedaremos. Si la incertidumbre es muy pequeña p<0.05% entonces tenemos seguridad de H1. Si la incertidumbre es muy grade p>0.05% entonces se da Ho. 

Hay una fuerte analogía con los juicios penales en el sistema legal: un acusado puede ser declarado presunto culpable, pero nadie es declarado inocente, simplemente no se ha demostrado que sea culpable. Del mismo modo, encontramos que podemos rechazar la hipótesis nula, pero si no tenemos evidencias suficientes para hacerlo, no significa que podamos aceptarla como verdad. Es solo una suposición de trabajo hasta que algo mejor aparece con el diseño experimental.

En situaciones complejas no es tan sencillo averiguar si los datos son compatibles con la hipótesis nula, quizá las pruebas de permutación puedan reducir la matemática de la complejidad. Si repetimos un proceso de asignación aleatoria de comportamiento de un evento (lanzar una moneda justa por ejemplo), si lo hace más por 1000 veces, y luego observamos su distribución de diferencias que genera, los resultados muestran una dispersión de las diferencias observadas —algunas favorecen caras o tras cruz— centradas en una diferencia de cero. La diferencia observada real se encuentra cerca del centro de esta distribución. Si fuera posible un enfoque con mucho tiempo disponible para trabajar sistemáticamente a través de todas las permutaciones posibles en lugar de simplemente hacer 1000 lanzamientos. Cada uno de ellos generaría una diferencia observada en proporción caras y cruz, y trazarlos producen una distribución más suave que para 1000 simulaciones. 

Desafortunadamente hay un gran número de permutaciones de este tipo, e incluso si se calcula un mil millón por segundo. Afortunadamente no tenemos que realizar estos cálculos ya que la distribución de probabilidad para esta diferencia observada en proporciones bajo la hipótesis nula se puede resolver en teoría, se basa en lo que se conoce como distribución hipergeométrica, que da la probabilidad de que cada lanzamiento acoja cada valor posible bajo permutaciones aleatorias^[33]: 

La distribución hipergeométrica, en cada lanzamiento de moneda de un conjunto de monedas, cambia la probabilidad de cada evento subsiguiente porque no hay reemplazo.  Las diferencias observadas reales en las promociones de caras o cruces se encuentra bastante cerca del centro de la distribución de las diferencias observadas que esperaríamos ver, si en realidad no hubiera ninguna asociación en absoluto. Necesitamos una medida para resumir cuán cerca del centro se encuentra nuestro valor observado, y un resumen es la “zona de cola” a la derecha de la línea de central de la distribución. 

Esta zona de cola se conoce como un valor p, uno de los conceptos más prominentes en las estadísticas practicadas hoy en día, y que por lo tanto merece una definición formal: un valor p es la probabilidad de obtener un resultado al menos tan extremo como nosotros, si la hipótesis nula (y todas las demás suposiciones del modelado) son realmente ciertas.  Molina Arias lo sintetiza así^[34]:

“Valor p: es una simple medida de la probabilidad de que la diferencia de resultado se deba al azar […] si la probabilidad es alta, diremos que la diferencia se debe al azar y que no es probable que se cumpla en la población. Pero si la probabilidad de obtener este valor por azar es muy baja, podremos decir que, probablemente, sí existe una diferencia real. Dicho de otro modo, rechazaremos la hipótesis nula y abrazaremos la alternativa. El valor de p tiene relación con la fiabilidad del estudio, cuyo resultado será más fiable cuanto menor sea la p.”

https://es.wikipedia.org/wiki/Valor_p

1.6.4.1 Significancia estadística 

Esta idea es sencilla: si un valor p es lo suficientemente pequeño, entonces decimos que los resultados son estadísticamente significativos. Este término fue popularizado por Ronald Fisher en 1920 y, a pesar de las críticas que veremos en el Módulo 3, sigue desempeñando un papel importante en las estadísticas. 

Ronald Fischer era un hombre extraordinario, pero difícil. Fue extraordinario porque es considerado pionero en dos campos: la genética y la estadística. Sin embargo, tenía un temperamento notorio y podía ser extremadamente crítico con cualquiera que sintiera que cuestionaba sus ideas, mientras que su apoyo a la eugenesia (sir Francis Galton, palabra que, literalmente, significa “ciencia del buen nacer”) y sus críticas públicas a la evidencia del vínculo entre el tabaquismo y el cáncer de pulmón que dañaron su posición. Su reputación personal ah sufrido a medida que sus conexiones financieras con la industria tabacalera han sido reveladas, pero como científico sus ideas encuentran aplicaciones en el análisis de grandes conjuntos de datos. "Hay solo unos pocos eruditos en cualquier disciplina que son simultáneamente reclamados por múltiples disciplinas como propios. La gran mente John von Neumann es uno de esos eruditos. El premio mayor en ciencias de la computación es un tributo a su liderazgo y erudición en el desarrollo de computadoras y su programación. Los físicos lo recuerdan por sus contribuciones, y el Proyecto Manhattan se basó en su experiencia en ingeniería química. Fue discípulo de David Hilbert y un matemático extraordinario, y fue quizás el padre más importante de la teoría de juegos que aportó tanto a tantas disciplinas. Finalmente, es reconocido como uno de los economistas más inteligentes que también hizo contribuciones significativas a la teoría financiera. Ronald Fisher comparte con von Neumann esta característica única de reconocimiento por parte de académicos de muchas disciplinas^[35]".

Fisher desarrollo la idea de la aleatorización en ensayos agrícolas. Ilustró las ideas de aleatorización en el diseño experimental con su famosa prueba de degustación de té^[36].

La carrera de muchos científicos experimentales depende del cálculo de los valores P a partir del análisis estadístico de sus datos, ya sea en psicología, geología o biología.  Incluso dentro de la quimiometría tradicional, los valores de P tienen algún papel, por ejemplo, para determinar si un factor en un experimento tiene una influencia significativa en la respuesta o si un compuesto marcador potencial es significativo. Sin embargo, la base de los valores de P no se comprende bien. La comprensión de la historia y la base de los valores P es esencial para la interpretación de gran parte de la ciencia experimental moderna.

Para apreciar el valor P, debemos mirar hacia atrás históricamente. Una especie en la jungla existe mucho antes de que un explorador la descubra y la nombre. Por lo tanto, el uso de lo que ahora llamaríamos valores P se informó dos siglos antes de su definición estadística formal.

• John Arbuthnot a principios del siglo XVIII1 analizó el número de hombres y mujeres nacidos a más de 82 años, registrado en Londres, y encontró que cada año había más hombres que mujeres^[37]. Argumentó que si fuera igualmente probable que el número de machos supere el número de hembras, las posibilidades de que esto suceda serían 0.582 o alrededor de 2 × 10⁻²⁵. En una analogía moderna (por supuesto, no conocida por Arbuthnot), se estima que han pasado alrededor de 1.4 × 10¹⁴ años desde el origen del Big Bang de nuestro universo, por lo que este evento sucedería solo una vez cada 100 mil millones de universos. Claramente, Arbuthnot concluyó que era extremadamente improbable que la posibilidad de que hombres y mujeres fueran registrados fuera igual, y concluyó que esto se debía a la providencia divina. En el razonamiento moderno, de hecho aceptaríamos que es inconcebible que las posibilidades de que hombres y mujeres sean registrados cada año sean iguales, pero en lugar de la providencia divina, podríamos pensar en otras razones, por ejemplo, que sea un asunto genético en ese momento o que en esa época las hembras tenían más probabilidades de ser asesinadas o regaladas al nacer que los machos. Sin embargo, el número de Arbuthnot 2 × 10⁻²⁵ es lo que llamaríamos un valor P.

Posteriormente, varios científicos y matemáticos han introducido conceptos relacionados, incluidos Daniel Bernoulli^[38] y Pierre Laplace^[39], ambos importantes en la historia del análisis de datos estadísticos moderno. Sin embargo, muchos conceptos estadísticos aparecen en la literatura a lo largo de los siglos, pero no se reconocen ni se formulan como ideas principales hasta décadas o incluso más tarde. En los primeros días de la ciencia, no era posible comunicarse bien; muchos estaban aislados unos de otros en sus propios países, con acceso a bibliotecas impresas localizadas y bastante especializadas, por lo que las ideas no podían viajar con mucha facilidad.

No fue hasta el siglo XX que se formuló el uso de valores P. Se atribuye a Karl Pearson, la primera persona en el mundo en establecer un departamento dedicado a las estadísticas, en el University College de Londres, ser el primero en formular el concepto en el contexto de la distribución .

Fue a través de Ronald Fisher, principalmente activo durante las décadas de 1920 y 1930, quien estableció muchos de los componentes básicos de las estadísticas modernas y quien formuló muchos de los conceptos, que casi un siglo después, todavía mantenemos. En su importante libro^[40], presenta a Lady Tasting Tea, que todavía se considera un experimento clásico en la estadística inferencial moderna. En Inglaterra en el siglo XX, era tradicional mezclar leche con té. Los orígenes de este hábito bastante excéntrico se han explicado de varias maneras, pero probablemente no se debió principalmente al sabor, uno es que la leche enfrió el té evitando que las delicadas tazas de porcelana se rompieran con el calor, otro que el té era caro y la leche barata diluía el bebida. Sin embargo, se afirmó que el té tiene un sabor diferente si se agrega leche a la taza antes o después del té. Hay algo de química sólida detrás de esto, agregar leche después significa que se encuentra inmediatamente con un líquido caliente y se desnaturaliza, mientras que al agregarlo antes, comienza a enfriarse y se calienta lentamente. Por brevedad, no discutiremos la química más aquí. Una psicóloga, Muriel Bristol, que trabajaba en el mismo instituto que Fisher, afirmó que podía notar la diferencia entre tazas de té con leche añadida antes y después, por lo que se propuso investigar esto. Se le presentaron ocho tazas de té, en orden aleatorio, cuatro con leche agregada después y cuatro antes, y se le pidió que eligiera las cuatro tazas preparadas por uno de los métodos; se le dice de antemano que habrá cuatro tazas de cada tipo, pero no cuál de ellas es de cada tipo. En el experimento, eligió las cuatro tazas correctamente. Entonces, ¿qué tan probable era que Muriel Bristol realmente tuviera la capacidad de determinar si se agregó leche primero o su elección pudo haber sido por casualidad?

1.6.4.2 Hipótesis nula 

El análisis de Fisher consistió en formular primero lo que llamó la "hipótesis nula". Esto fue que Muriel Bristol no pudo distinguir entre agregar leche antes o después. La pregunta que luego planteó es, si ella no pudo distinguir cuándo se agregó la leche, ¿qué probabilidad hay de que obtenga el resultado experimental de identificar cuáles 4 de las 8 tazas se prepararon correctamente con un método por casualidad? Este es un tipo de pregunta muy similar a la que Arbuthnot hizo unos 200 años antes, ¿qué tan probable era que hubiera más nacimientos de hombres que de mujeres registrados en Londres durante cada uno de los 82 años si las posibilidades de que naciera un hombre y una mujer fueran iguales? Si Muriel Bristol no pudo distinguir, las posibilidades de que obtenga el resultado están dadas por 4! (8-4)! / 8! = 1/70 = 0.014 usando combinatorias. Por lo tanto, se esperaría que obtuviera su resultado solo una vez en 70, y el valor 0.014 se define como un valor P.

Dado que Muriel Bristol identificó correctamente las 4 tazas, Fisher afirmó que era muy poco probable que esto fuera por casualidad si no tenía una capacidad subyacente para diferenciar entre cada método y, como tal, rechazó la llamada hipótesis nula; Abogó por que cualquier valor P menor que 0.05 es una buena evidencia de que la hipótesis nula no es un modelo verdadero para los resultados experimentales.

1.6.4.3 Consecuencias 

Son muchas las consecuencias de esta descripción original.

• la primera se relaciona con el diseño experimental. El experimento de degustación de té tenía que incluir suficientes tazas. Si solo se hubieran usado cuatro tazas, dos con leche agregada antes y dos después, incluso si Muriel Bristol eligió dos correctamente, esto podría haber sucedido una vez de cada seis, con un valor P del 17%, si la hipótesis nula fuera correcta. Por tanto, el tamaño del experimento habría sido inadecuado.

• En lugar de probar la hipótesis “Muriel Bristol puede notar la diferencia”, defendió que es mejor probar “Muriel Bristol no puede notar la diferencia” y ver si es probable que esto sea correcto. La hipótesis nula es como una hipótesis exacta, que es más fácil de probar.

• Digamos que estamos interesados en saber si la estatura promedio de los hombres en dos pueblos es la misma y tomamos una muestra de 10 de cada uno. La hipótesis nula es que la diferencia subyacente (población) es 0, este es un número exacto y estamos interesados ??en la probabilidad de que nuestra muestra sea compatible con esto. Es mucho más difícil determinar si la diferencia de alturas de la población es de 2 o 5 cm, por lo que en su marco, es mucho más fácil probar la suposición nula en lugar de determinar una hipótesis alternativa.

• Regrese a las observaciones de Arbuthnot sobre los nacimientos de hombres y mujeres en Londres. Podía probarse con bastante facilidad si sus registros eran compatibles con la hipótesis nula exacta de que había las mismas posibilidades de nacimientos de hombres y mujeres a lo largo de 82 años, pero habría sido mucho más difícil determinar si esto se debió a la providencia divina o si los padres no hicieron registros de los niñas porque eran económicamente menos útiles en ese momento.

• Para un uso significativo de los valores P, es esencial definir primero una hipótesis nula sensible; en el caso de Lady Tasting Tea, esto es bastante fácil, pero en muchas situaciones científicas prácticas, no siempre es así.

En términos modernos, para cualquier conjunto de observaciones experimentales, primero formulamos una hipótesis nula. Por supuesto, debe ser útil y, por lo general, se obtiene a partir de conocimientos científicos previos. Por ejemplo, puede que nos interese un metabolito y nuestra hipótesis nula es la distribución de este metabolito en pacientes sanos (a menudo llamados controles). Luego obtenemos un valor experimental para la concentración del metabolito en un donante y calculamos con qué frecuencia se observaría al menos a esta concentración en la población de control (sana o nula). Este es el valor P, y si es bajo (a menudo menor de 0.05 o ocurriría menos de 1 de cada 20 en la población de control al menos en el valor observado experimentalmente), decimos que el valor es menor de 0.05, y esto es una buena evidencia para rechazar la hipótesis nula, por lo que es poco probable que el donante sea miembro de la población de control. Por supuesto, si evaluamos a cientos de pacientes sanos, esperamos algunos valores extremos, por lo que el valor P debe interpretarse con precaución.

1.6.4.4 Ilustración gráfica

Gráficamente, los valores de P se pueden ilustrar como en la Figura 1.4.

• La curva azul es la distribución nula hipotética.

• El área bajo esta curva se puede representar mediante una distribución de densidad de probabilidad (pdf) del área 1 y está sombreada en azul.

• Se indica una medición experimental y el área bajo la curva mayor que esta se sombrea en azul oscuro.

• En el caso ilustrado, el área azul oscuro es igual a 0.03.

• Por lo tanto, si la medición experimental se tomó como muestra de la distribución nula, solo esperaríamos obtener un valor de este tamaño o más el 3% del tiempo, dando el valor P.

Por supuesto, los valores de P no están restringidos a distribuciones normales o incluso continuas.

Figura 1.4Ilustración de un valor P de una cola de 0.03 con una distribución nula de Gaus

• En el caso de Lady Tasting Tea, la cantidad de formas en que puede elegir N tazas correctamente, si se le dan nuestras opciones, es (4! /[(4-N)! ¡N!])²

• La probabilidad entonces se convierte en {4! / [(4-N)! N!]²} / 70 calculado en la Tabla 1; para más detalles del cálculo, consulte el estudio anterior o cualquier número de páginas web o textos.

• En la columna de la derecha, calculamos lo que llamamos el valor P de una cola, para cualquiera de los posibles resultados.

• Esto se ilustra en la Figura 1.5 en el caso de que al menos tres de cada cuatro de los vasos seleccionados estén correctamente asignados, lo que corresponde a un valor P de 0,243; en otras palabras, usando la hipótesis nula de que la señora no puede distinguir si la leche se agrega antes o después, aún podría identificar tres o más de las tazas correctamente alrededor de una de cada cuatro.

Tabla 1.1 Probabilidad de cada resultado para Lady Tasting Tea

Figura 1.5 El valor P correspondiente a la obtención de tres o más de cuatro tazas de té correcto

Figura 1.5 Ilustración de un valor P de dos colas de 0.4 con una distribución nula de Gauss

VALORES P DE DOS COLAS

Los valores de P también pueden ser de dos colas.

• Para una prueba de una cola, como se ilustra arriba, podríamos hacer una pregunta como "¿Cuál es el valor P de que la altura de un hombre de una aldea es más de 2 metros?"

• Sin embargo, para un valor de P de dos colas, podríamos preguntar "¿cuál es el valor de P para que la altura de un hombre esté dentro de los 10 cm del valor medio de los hombres de esta aldea?"

• En la Figura 1.5, ilustramos un valor P de dos colas de 0.4. Una muestra estará fuera del área celeste cuatro veces de cada 10 si la distribución nula es un modelo correcto y, por lo tanto, no es tan raro.

• Por lo tanto, si una muestra tiene un valor P de 0.4 o 0.2 puede depender de cómo se plantee el problema y del objetivo del análisis.

Estadísticas multivariadas

En la estadística multivariante, no hay dirección, puede ser necesario utilizar un valor de P multidireccional. Lo que es apropiado depende de la pregunta que se haga. Por ejemplo, si estamos interesados ??en si un error es significativamente mayor que la media, estamos interesados ??en un valor P de una cola, pero si estamos interesados ??en si una muestra es miembro de un grupo basado en mediciones multivariadas, a menudo no están interesados ??en la dirección de la desviación. Los valores  P para distribuciones multivariadas pueden ser muy complicados de calcular y están fuera del alcance de la estadística básica, especialmente si existe correlación entre las variables. La mayor parte de la literatura tradicional sobre valores P se ilustra mediante distribuciones univariadas. El dilema para el observador es que suposiciones como la normalidad multivariante rara vez se obedecen, ni siquiera aproximadamente. Sin embargo, la comprensión de la historia y la base de los valores P es esencial para la interpretación de gran parte de la ciencia experimental moderna.

Ronald Fischer utilizó P<0.05 y P<0.01 como umbrales críticos convenientes para indicar la importancia, y produjo tablas de los valores críticos de las estadísticas de pruebas necesarias para alcanzar estos niveles de importancia. La popularidad de estas tablas llevó a que 0.05 y 0.01 se conviertan en convenciones establecidas, aunque ahora se recomienda que se informen los valores P exactos a condición no solo a la verdad de la hipótesis nula, sino también a todas las demás suposiciones subyacentes al modelo estadístico, como la falta de sesgo sistemático, las observaciones independientes, etc. 

Todo este proceso se ha conocido como Pruebas de Significado de Hipótesis Nulas (NHST por las siglas en inglés). 

Las principales diferencias entre las "pruebas de significación" de Fisher y las "pruebas de hipótesis" de Neyman Pearson. Nos dicen que ''en el razonamiento científico, la prueba más definitiva de una hipótesis es el silogismo del modus tollensor “prueba por contradicción'' y que '' esta es también la forma lógica utilizada en NHST, sin embargo, el problema crucial es que el modus tollens se vuelve formalmente incorrecto con declaraciones probabilísticas que pueden llevar a conclusiones seriamente incorrectas''.

En esta breve nota, señalo un importante ingrediente que falta en la aplicación del silogismo del modus tollens a la Prueba de significación de hipótesis nulas (NHST) utilizada por el artículo original de Schneider^[41] y la respuesta de Schneider al comentario de Wu^[42] en el artículo original de Schneider.

El silogismo del modus tollens es el siguiente:

  Esquema (1)

Es decir, sí "A implica B" y "B no es cierta”, entonces concluya que "A no es cierta”. Modus tollens es un procedimiento de inferencia válido y a menudo se emplea en inferencia estadística, especialmente en NHST, en el siguiente sentido: sí A es un supuesto que implica un evento observable B (obtenido a partir de un experimento) y, después de realizar el experimento, se sí observamos la negación de B, entonces debemos concluir que nuestro supuesto A no es verdadero. Schneider proporciona el siguiente esquema para aplicar el modus tollens en NHST:

Premisa 1: Si Ho (es decir, A) es verdadera, entonces Q (es decir, B) es muy probable ...

Premisa 2: No-Q (es decir,: B) ...

Conclusión: Ho es muy poco probable.  

Esquema (2)    

La afirmación Q se refiere a que el valor p es mayor que un cierto valor umbral (el nivel de significancia). Al utilizar el esquema (2) e interpretar los valores p como probabilidades condicionales, se concluye que: “… dado que NHST se basa en una probabilidad condicional sola y se enmarca en un marco de razonamiento probabilístico modus tollens, es por definición lógicamente inválido''. Para ilustrar el esquema (2) en notación estadística, consideremos la hipótesis nula , los datos observados y un estadístico de prueba positivo que ordena el espacio muestral en el siguiente sentido: cuanto más discrepante es Ho de los datos observados x, mayor es el valor observado ; por ejemplo, ; donde es la estadística de razón de verosimilitud y es la función de verosimilitud. La siguiente definición del valor P satisface los requisitos de Fisher para las pruebas de significancia:

Es bien sabido que, bajo Ho y algunas condiciones regulares en el modelo estadístico y en la geometría de , asintóticamente tiene una distribución uniforme. El valor p es la probabilidad de observar un evento extremo en el mejor escenario de Ho. Además, es digno de mención que el valor p no es una probabilidad condicional dada Ho como se indica típicamente. No es correcto operar el valor p anterior como si fuera una probabilidad condicional genuina, ya que los eventos Ho y no son medibles en el mismo espacio y, por lo tanto, la probabilidad condicional no debe emplearse para ellos. Las conclusiones sobre la validez de los valores p basadas en argumentos de probabilidad condicional son más incorrectas en el dominio de los marcos clásico o frecuentista (utilizamos el término "marco clásico" cuando el modelo estadístico clásico se emplea como herramienta matemática sin adoptar necesariamente el paradigma frecuentista).

Volvamos al esquema (2). Tenga en cuenta que se puede reescribir en términos de declaraciones estadísticas como

Esquema (3)

El problema con (3) es que la hipótesis nula Ho no puede garantizar por sí sola que , ya que podríamos haber observado un evento "raro" bajo Ho tal que . Es decir, no es el caso de que Ho implique . Por lo tanto, el silogismo de modus tollens no debe aplicarse en esquema (3). Además, esta línea de razonamiento no representa la disyunción de Fisher sobre un resultado significativo: "o ocurrió un evento raro o Ho no es cierta^[43]”. El ingrediente que falta en (3) se analiza a continuación.

Sea un subconjunto del espacio muestral que indica el evento raro relevante bajo la hipótesis nula Ho tal que implica . Tomamos A como el enunciado ‘‘’’ y B el enunciado ‘‘’’, entonces el silogismo presentado en la Ec. para una prueba de significancia debe leerse como sigue

Esquema (4)

El enunciado completo (4) se interpreta en un lenguaje sencillo como sigue: siempre que x no sea un evento raro y la hipótesis nula H₀ sea verdadera, entonces . Sin embargo, si observamos , entonces debemos concluir que ocurrió un evento raro o que H₀ no es cierto. Esto me parece muy razonable.

El esquema (4) sugiere que es responsabilidad del analista decidir si un resultado significativo es relevante. No debemos culpar a la herramienta estadística cuando en realidad el problema radica en otro dominio. El factor humano debe considerarse más seriamente, ya que parece ser común en la ciencia moderna que algunos experimentos no sean reproducibles^[44] y también tienden a sobreestimar los tamaños del efecto^[45]. Además, aunque el valor P habitual tiene algunos problemas técnicos, pueden evitarse redefiniéndolo mediante conjuntos de confianza^[46].

En síntesis 

1. Las pruebas de hipótesis nulas (suposiciones predeterminadas sobre modelos estadísticas) forman una parte importante de la práctica estadística.

2. Un valor P es una medida de la incompatibilidad entre datos observados y una hipótesis nula: formalmente es la probabilidad de observar un resultado resultado tan extremo, si la hipótesis nula fuera cierta.

3. Tradicionalmente, se han establecido umbrales de P-valor 0.05 y 0.01 para declarar la significancia estadística.

4. Estos umbrales deben ajustarse si se realizan varias pruebas, por ejemplo, en diferentes subconjuntos de datos o en múltiples medidas de resultados.

5. Hay una correspondencia precisa entre intervalos de confianza y valores P: si, por ejemplo, el intervalo del 95% excluye 0, podemos rechazar la hipótesis nula de 0 en P<0.05.

6. Se han desarrollado de manera separada formas de pruebas de hipótesis para pruebas secuencia.

7. Los valores P a menudo se malinterpretan: en particular, no transmiten la probabilidad de que la hipótesis nula sea verdadera, ni que un resultado no significativo implica que la hipótesis nula sea cierta.

1.7 La ciencia de datos 

La causalidad ha experimentado una transformación importante, de un concepto envuelto en misterio, a en un objeto matemático con semántica bien definida y lógica bien fundada^[47]. La ciencia de datos ha cambiado la forma en que distinguimos los hechos de la ficción y, sin embargo, ha permanecido bajo el radar de las universidades y la sociedad en general. Las consecuencias de esta ciencia ya están afectando facetas cruciales de nuestra vida y tiene un potencial aún mayor, el diseño de fármacos, fertilizantes, políticas económicas, control de la violencia y el calentamiento global^[48]. La inferencia causal, la probabilidad subjetiva y lenguajes informáticos como R, se trata de tomar muy enserio emular la razón de nuestra mente y hacer de la pregunta ¿Por qué? el motor matemático de sus métodos. Consideramos que el cerebro humano es la herramienta más potente para el manejo causal. La memoria está llena de causas y efectos reconocido en la experiencia de nuestra vida; se mejora con nuevos datos, aprovecha la lógica detrás de neutros pensamientos causales, emula esta lógica en computadoras y crea la Inteligencia Artificial y las Máquinas de Aprendizaje. 

Las herramientas bayesianas de la probabilidad subjetiva, nos permiten nuevos experimentos y extraer continuamente más datos, procesarlos (información) y sacar inferencias de conclusión causal. ¿Qué tan eficaz es un tratamiento para combatir una enfermedad? ¿Los nuevos reglamentos hacen que aumente el desempeño académico de universidades o gobiernos? ¿Cuál es el daño atribuible al intelecto de los estudiantes que con énfasis realizan plagio en sus trabajos académicos? ¿Pueden los registró de atención al público demostrar discriminación sexual? ¿Debería dejar de producir libros en el tema de STEM, cuando no hay interés alguno por la autoridad universitaria?

Estas preguntas tienen un factor común, la relación causa-efecto reconocible a través de palabras como prevenir, causa, atribuible a, política y debería yo. La ciencia de datos a transformado este lenguaje común en objetos matemáticos en la importante inferencia causal. Las relaciones causales se escriben en lenguaje matemático y se desarrollan en métodos para lidiar con la incertidumbre de responder a causales. El arte del diseño experimental basado en la filosofía de Bayes resuena en las publicaciones de biología experimental, estudios de redes bayesianas bioquímicas, internet, eléctricas, genéticas… y, en el centro de atención a la eficacia de las políticas publicas de gobiernos. Esta ciencia de datos no se pudo desarrollar antes, porque la tecnología computacional no se encontraba en una madurez como la actual. 

Fueron Francis Galton y Karl Pearson, quienes por primera vez descubrieron que los datos de poblaciones pueden arrojar luz sobre cuestiones científicas. Hay además, una larga historia detrás de su desafortunado fracaso en aceptar la causalidad en esta coyuntura de su tiempo. Esto retrasó el progreso del vocabulario tradicional científico, solo se comunicaba a las ideas hipotético deductivas, pero, las nuevas formas científicas de vocabulario con verdades entre uno y cero de probabilidad, lanzan preguntas causales hipotético inductivas que revolucionan la ciencia. Irónicamente, la necesidad de una teoría de la causalidad comenzó a surgir al mismo tiempo que las estadísticas surgieron con fuerza. De hecho, las estadísticas modernas surgieron de las preguntas causales Galton y Pearson hicieron sobre sus ingeniosos intentos de responder preguntas utilizando datos de intergeneraciones de poblaciones. Este fue un momento crítico para la ciencia. La oportunidad de hacer preguntas causales y responder con verdades graduadas entre cero y uno. En los años siguientes, fueron declaradas poco científicas y pasaron a la clandestinidad. A pesar de los esfuerzos heroicos del genetista Sewall Writht (1889-1988), el vocabulario causal estuvo virtualmente prohibido durante más de medio siglo. Y cuando prohibes el habla, prohíbes los principios fundamentales de ese pensamiento y se asfixia en la cultura métodos y herramientas intelectuales.

Los lectores no tiene que ser científicos para ser testigos de esta prohibición. La frase “la correlación no es casual”, tendría que esperar a su discusión, y con ello el nacimiento de la inferencia causal.

Por el tipo de curso clásico de estadística en su modo en que se aborda, el estudiante se le permite decir X está relacionada con Y, X esta asociada con Y, pero no X es causal de Y. Debido a esta restricción, las herramientas matemáticas para gestión de causales se consideran necesarias y hacen de las estadísticas solo un resumen de datos, no en cómo interpretarlos. Una excepción brillante fue el análisis de caminos (path), inventado por Sewall Writht en 1920. Sin embargo el método de path fue subestimado en las estadísticas y sus comunidades por décadas, y fue hasta 1980 que la inferencias causal se abrió camino, cuando se hace conciencia que la falsa repuesta a las preguntas científicas residen en los datos, que se revelarían a través de ingeniosos trucos de mentira de datos. 

Los datos pueden decir que una planta que se aplicó un químico se recupero de una infección más rápido que aquellas que no se expusieron, pero no puede decirle por qué. Cada vez en la ciencia y las empresas industriales se observo que los meros datos no son suficientes. Hoy en día, gracias a modelos causales cuidadosamente elaborados, los científicos contemporáneos pueden abordar problemas que alguna vez se habrían considerado irresolubles o incluso más allá de la pálida investigación científica. Hace cien años no consideró afirmar que fumar tabaco era causa de un peligro para salud, porque esta proporción resultaba poco rigurosa en la ciencia. La mera mención de la palabra causal o efecto, crearía una tormenta de objeciones en cualquier publicación científica de buena reputación.

Pero hoy en día, epidemiológicos, biólogos, científicos sociales, informáticos y economistas plantean tales preguntas rutinariamente y las responden con precisión matemática. Este cambio a solo 20 años, conduce a una ciencia de datos de probabilidad subjetiva que abraza el don cognitivo innato de nuestra mente causal para proponer efectos. Este cambio en el diseño experimental no ocurrió en el vacío; tiene un secreto matemático detrás que puede describirse como cálculo causal. Responde a los problemas de relaciones causa-efecto. Este potencial matemático transformó la investigación biología en una ciencia de precisión matemática.

El cálculo de la causalidad consta de dos objetos: grafos casuales, para expresar lo que sabemos, y un lenguaje simbólico, parecido al álgebra, para expresar lo que queremos saber. Los diagramas causales son simplemente grafos de nodos y flechas que resumen nuestro conocimiento científico existente dentro de redes causales. Los nodos representan cantidades o variables de interés y las flechas o ramas representan interacciones causales entre variables y cadenas o path a saber, qué variables escuchan la interacción a qué otras transmiten el efecto. Se puede navegar en los grafos utilizando nodos y ramas como calles unidireccionales, se pueden comprender los grafos como vías causales y resolver el tipo de preguntas qué causa qué. 

Referencias

[1] Lee, Hyo & Chung, Yoon & Jang, Sungbong & Seo, Dong & Lee, Hak & Yoon, Duhak & Lim, Dajeong & Lee, Seung. (2020). Genome-wide identification of major genes and genomic prediction using high-density and text-mined gene-based SNP panels in Hanwoo (Korean cattle). PLOS ONE. 15. e0241848. 10.1371/journal.pone.0241848.

[2] Allen, Hana & Estrada, Karol & Lettre, Guillaume & Berndt, Sonja & Weedon, Michael & Rivadeneira, Fernando & Willer, Cristen & Jackson, Anne & Vedantam, Sailaja & Raychaudhuri, Soumya & Ferreira, Teresa & Wood, Andrew & Weyant, Robert & Segrè, Ayellet & Speliotes, Elizabeth & Wheeler, Eleanor & Soranzo, Nicole & Park, Ju-Hyun & Yang, Jian & Hirschhorn, Joel. (2010). Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature. 467. 832-8. 10.1038/nature09410.

[3] Littlefield, Joanne. (2013). Howard Wainer: A review of four books. Visual Studies. 28. 10.1080/1472586X.2013.765222.

[4] Crowther, T. W., Glick, H. B., Covey, K. R., Bettigole, C., Maynard, D. S., Thomas, S. M., . . . Amatulli, G. (2015). Mapping tree density at a global scale. Nature, 525(7568), 201.

[5] Simmons, J. P., & Simonsohn, U. (2017). Power posing: P-curving the evidence. Psychological science.

[6] Anderson, D. R., & Burnham, K. P. (1999). General strategies for the analysis of ringing data. Bird study.

[7] Blyth, Stephen. (1994). Karl Pearson and the Correlation Curve. International Statistical Review. 62. 10.2307/1403769.

[8] Norton, Bernard. (1979). Charles Spearman and the general factor in intelligence: Genesis and interpretation in the light of sociopersonal considerations. Journal of the history of the behavioral sciences. 15. 142-54. 10.1002/1520-6696(197904)15:23.0.CO;2-X.

[9] https://esa.un.org/unpd/wpp/Download/Standard/Population/. 6.   ONS popular names is at https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/livebirths/bulletins/babynamesenglandandwales/2015.

[10] Cuffe, Paul. (2019). Data Visualization: A Practical Introduction. IEEE Transactions on Professional Communication. PP. 1-2. 10.1109/TPC.2019.2922787.

[11] Knepper, David. (1944). A Guide to Public Opinion Polls. By George Gallup. Journal of Politics - J POLIT. 6. 10.2307/2125722.

[12] Talbäck, Mats & Brooke, Hannah & Mogensen, H & Mathiesen, Tiit & Feychting, Maria & Ljung, Rickard. (2017). Socioeconomic position and mortality from brain tumour – A Swedish national cohort study. European Journal of Public Health. 27. 10.1093/eurpub/ckx187.456.

[13] Khanolkar, Amal & Ljung, Rickard & Talbäck, Mats & Brooke, Hannah & Carlsson, Sofia & Mathiesen, Tiit & Feychting, Maria. (2016). Socioeconomic position and the risk of brain tumour: A Swedish national population-based cohort study. Journal of Epidemiology and Community Health. 70. jech-2015. 10.1136/jech-2015-207002.

[14] https://www.tylervigen.com/spurious-correlations

[15] Brereton, Richard. (2020). P values and Ronald Fisher. Journal of Chemometrics. 10.1002/cem.3239.

[16] Malinowski, Jacek. (2005). Logic of Simpson paradox. Logic and Logical Philosophy. 14. 10.12775/LLP.2005.013.

[17] Modica, Salvatore & Pennisi, Aline. (2009). The Simpson paradox of school grading in Italy. Research in Economics. 63. 91-94. 10.1016/j.rie.2009.04.004.

[18] Petit, J.L.. (1992). Generalization of the Simpson paradox. Revue de Statistique Appliquée. 40.

[19] https://es.wikipedia.org/wiki/Paradoja_de_Simpson

[20] Alshamlan, Hebah & Alqadeeb, Maha & Alwabel, Sarah & Aljbreen, Munerah. (2020). House Price Prediction.

[21] Masip, J. & Lluch, J.R.. (2019). Alcohol, health and cardiovascular disease. Revista Clínica Española (English Edition). 10.1016/j.rceng.2019.07.001.

[22] Huang, Dayan & Hunter, Zoë & Francescutti, Louis. (2012). Alcohol, Health, and Injuries. American Journal of Lifestyle Medicine. 7. 232-240. 10.1177/1559827612468836.

[23] Gardner, M.. (1985). A Short Textbook of Medical Statistics. by Austin Bradford Hill. Journal of the Royal Statistical Society. Series A (General). 148. 170-171. 10.2307/2981960.

[24] Gardner, M.. (1985). A Short Textbook of Medical Statistics. by Austin Bradford Hill. Journal of the Royal Statistical Society. Series A (General). 148. 170-171. 10.2307/2981960.

[25] Dudbridge, Frank. (2020). Polygenic Mendelian Randomization. Cold Spring Harbor Perspectives in Medicine. a039586. 10.1101/cshperspect.a039586.

[26] Senn, Stephen. (2011). Francis Galton and regression to the mean. Significance. 8. 124 - 126. 10.1111/j.1740-9713.2011.00509.x.

[27] Saito, Chihiro & Minami, Yuichiro & Arai, Kotaro & Haruki, Shintaro & Shirotani, Shota & Higuchi, Satoshi & Ashihara, Kyomi & Hagiwara, Nobuhisa. (2020). Prognostic Significance of the Mitral L-Wave in Patients With Hypertrophic Cardiomyopathy. The American Journal of Cardiology. 10.1016/j.amjcard.2020.05.040.

[28] Nwanganga, Fred & Chapple, Mike. (2020). Logistic Regression. 165-219. 10.1002/9781119591542.ch5.

[29] Jones, Stephen. (2014). George Box and Robust Design. Applied Stochastic Models in Business and Industry. 30. 10.1002/asmb.2023.

[30] https://es.wikipedia.org/wiki/Teorema_del_l%C3%ADmite_central

[31] Wild, C.J. y Pfannkuch, M. (1999). Statistical Thinking in Empirical Enquiry. International Statistical Review (1999), 67, 3, 223-265

[32] Luciano, Giorgio. (2021). Design of Experiment. 10.1201/b21873-4.

[33] https://es.wikipedia.org/wiki/Distribución_hipergeométrica

[34] Molina Arias, M. (2017). ¿Qué significa realmente el valor de p?. Pediatría Atención Primaria, 19(76), 377-381. Recuperado en 06 de marzo de 2021, de http://scielo.isciii.es/scielo.php?script=sci_arttext&pid=S1139-76322017000500014&lng=es&tlng=es.

[35] Read, Colin. (2016). Later Life and Legacy of Ronald Fisher. 10.1057/978-1-137-34137-2_14.

[36] DEMPSTER, A.. (1979). Life and Work of Ronald Fisher. Science. 203. 537-537. 10.1126/science.203.4380.537

[37] Arbuthnott, John. (1710). An Argument for Divine Providence, Taken from the Constant Regularity Observ'd in the Births of Both Sexes. History of Economic Thought Articles. 27. 186-190. 10.1098/rstl.1710.0011.

[38] Bernoulli D. Recherches physiques et astronomiques. Pieces Qui Ont Remporte le Prix Double de l'Academie Royale Des Sciences en. 1735; 1734:93-122

[39] Laplace P. Mémoire sur les probabilités. Mémoires de l'Académie Royale Des Sciences de Paris. 1778;9:227-332.

[40] Fisher RA. The Design of Experiments. New York: Oliver and Boyd; 1935.

[41] Schneider, J. W. (2015). Null hypothesis significance tests. A mix-up of two different theories: The basis for widespread confusion and numerous misinterpretations. Scientometrics, 102, 411–432.

[42] Wu, J. (2018). Is there an intrinsic logical error in null hypothesis significance tests? Commentary on: ‘‘Null hypothesis significance tests. A mix-up of two different theories: The basis for widespread confusion and numerous misinterpretations’’. Scientometrics, 115, 621–625.

[43] Fisher, R. A. (1959). Statistical methods and scientific inference (2nd ed.). Edinburgh: Oliver and Boyd

[44] Nosek, Brian & Cohoon, Johanna & Kidwell, Mallory & Spies, Jeffrey. (2016). Estimating the Reproducibility of Psychological Science. 10.31219/osf.io/447b3

[45] Fanelli, Daniele & Costas, Rodrigo & Ioannidis, John. (2017). Meta-assessment of bias in science. Proceedings of the National Academy of Sciences. 114. 201618569. 10.1073/pnas.1618569114.

[46] Patriota, Alexandre. (2018). Is NHST logically flawed? Commentary on: “NHST is still logically flawed”. Scientometrics. 116. 10.1007/s11192-018-2817-4.

[47] Markus, Keith. (2021). Causal effects and counterfactual conditionals: contrasting Rubin, Lewis and Pearl. Economics and Philosophy. 1-21. 10.1017/S0266267120000437.

[48] Münch, Maximilian & Raab, Christoph & Biehl, Michael & Schleif, Frank-Michael. (2020). Data-Driven Supervised Learning for Life Science Data. Frontiers in Applied Mathematics and Statistics. 6. 10.3389/fams.2020.553000.

Autores:

Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Berenice Yahuaca Juárez
Erasmo Cadenas Calderón
Abraham Zamudio Durán
Lizbeth Guadalupe Villalon Magallan
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán
Monica Rico Reyes