Texto universitario

_____________________________

Módulo 3: Teoría de matrices 

3.1 Definiciones básicas y notación

A menudo es útil tratar las filas o columnas de una matriz como vectores. Términos como la independencia lineal que hemos definido para vectores también se aplican a filas y/o columnas de una matriz. El espacio vectorial generado por las columnas de la matriz A de n×m es de orden n y de dimensión m, se llama espacio columna de A, rango de A o variedad de A. Este espacio vectorial se denota por V(A) o span(A).

No hacemos distinción entre estas dos notaciones. La notación V(·) enfatiza que el resultado es un espacio vectorial. Tenga en cuenta que si A ∈ × m, entonces V(A) ⊆ .

El argumento de V(·) o span(·) también puede ser un conjunto de vectores en lugar de una matriz. Recordemos que si G es un conjunto de vectores, el intervalo de símbolos (G) denota el espacio vectorial generado por los vectores en G.

También definimos el espacio de fila de A como el espacio vectorial de orden m (y de dimensión n o menos) generado por las filas de A; observe, sin embargo, la preferencia dada al espacio de la columna.

Muchas de las propiedades de las matrices que discutimos son válidas para matrices con un número infinito de elementos, pero a lo largo de este libro asumiremos que las matrices tienen un número finito de elementos y, por lo tanto, los espacios vectoriales son de orden finito y tienen un número finito. de dimensiones.

Dada una matriz A  n × m con elementos a_ij, la matriz m × n con elementos a_ji se llama la transposición de A. Utilizamos un superíndice "T" para denotar la transposición de una matriz; así, si A = (a_ij), entonces

Si, en la matriz A con elementos a_ij para todos i y j, a_ij = a_ji, se dice que A es simétrica. Una matriz simétrica es necesariamente cuadrada. Una matriz A tal que se dice que a_ij=−a_ji es simétrica sesgada. Obviamente, las entradas diagonales de una matriz simétrica oblicua deben ser 0. Si (donde representa el conjugado del número complejo a), se dice que A es Hermitiano. Una matriz hermitiana también es necesariamente cuadrada con elementos reales en la diagonal y, por supuesto, una matriz simétrica real es hermitiana. Una matriz hermitiana también se denomina matriz autoadjunta.

3.1.1 Multiplicación de una matriz por un escalar

Similar a nuestra definición de multiplicación de un vector por un escalar, definimos la multiplicación de una matriz A por un escalar c como

3.1.2 Elementos diagonales

Los a_iielementos de una matriz se denominan elementos diagonales. Un elemento aij con i < j se dice que está "por encima de la diagonal", y uno con i> j se dice que está "por debajo de la diagonal". El vector que consta de todas las a_ii se llama diagonal principal o simplemente diagonal. Esta definición de diagonal principal se aplica tanto si la matriz que es cuadrada como a la que no.

Denotamos la diagonal principal de una matriz A por diag(A) o por vectores vecdiag(A). La función diag o vecdiag definida aquí como un mapeo 

Si A es una matriz de n × m, y k = min (n, m),

Como se señaló anteriormente, también podemos denotar esto como vecdiag (A), pero generalmente usaremos  la notación “diag (·)”.

Tenga en cuenta de la definición que

y esto es cierto tanto si A es cuadrado como si no.

La diagonal comienza en la primera fila y la primera columna (es decir, a₁₁) y termina en a_kk, donde k es el mínimo del número de filas y el número de columnas.

Para c = ± 1,..., los elementos a_i,i+c se denominan "codiagonales" o "diagonales menores". Las codiagonales a_{i,i +1} se denominan “supradiagonales” y las codiagonales a_i,i−1se denominan “infradiagonales”. Si la matriz tiene m columnas, los elementos 

a_{i, m+1- i} de la matriz se denominan elementos diagonales oblicuos . Usamos términos similares a los de los elementos diagonales para los elementos por encima y por debajo de los elementos diagonales sesgados. Estas frases se utilizan con matrices cuadradas y no cuadradas.

3.1.3 Matrices diagonales y huecas

Si todos excepto los elementos diagonales principales de una matriz son 0, la matriz se denomina matriz diagonal. Una matriz diagonal es el tipo más común y más importante de "matriz dispersa". Si todos los elementos diagonales principales de una matriz son 0, la matriz se llama matriz hueca. Una matriz simétrica sesgada es hueca, por ejemplo. Si todos excepto los principales elementos diagonales oblicuos de una matriz son 0, la matriz se denomina matriz diagonal oblicua.

3.1.4 Matrices con patrones especiales de ceros

Si todos los elementos debajo de la diagonal son 0, la matriz se llama matriz triangular superior; y una matriz triangular inferior se define de manera similar. Si todos los elementos de una columna o fila de una matriz triangular son cero, todavía nos referimos a la matriz como triangular, aunque a veces hablamos de su forma como trapezoidal. Otra forma llamada trapezoidal es aquella en la que hay más columnas que filas, y las columnas adicionales posiblemente sean distintas de cero. Las cuatro formas generales de matrices triangulares o trapezoidales se muestran a continuación, utilizando una notación intuitiva con X y 0 para indicar el patrón.

En esta notación, X indica que el elemento posiblemente no es cero. No significa que todos los elementos sean iguales. En algunos casos, X y 0 pueden indicar "submatrices".

Si todos los elementos son 0 excepto a_{i, i + ck} para un pequeño número de enteros c_k, la matriz se llama matriz de bandas. En muchas aplicaciones, c_k ∈ {−w_l, −_wl + 1,. . . , −1, 0, 1,. . ., w_u - 1, w_u}. En tal caso, w_l se denomina ancho de banda inferior y w_u se denomina ancho de banda superior. Estas matrices con patrones surgen en series de tiempo y otros modelos de procesos estocásticos, así como en soluciones de ecuaciones diferenciales, por lo que son muy importantes en ciertas aplicaciones. Aunque a menudo ocurre que las matrices de bandas interesantes son simétricas, o al menos tienen el mismo número de codiagonales que no son cero, ninguna de estas condiciones siempre ocurre en aplicaciones de matrices de bandas. Si todos los elementos debajo de los principales elementos diagonales sesgados de una matriz son 0, la matriz se denomina matriz triangular superior sesgada. Una forma común de la matriz de Hankel, por ejemplo, es la matriz triangular superior sesgada. Observe que los diversos términos definidos aquí, como triangular y banda, también se aplican a matrices no cuadradas.

Las matrices de bandas ocurren a menudo en soluciones numéricas de ecuaciones diferenciales parciales. Una matriz de bandas con anchos de banda inferior y superior de 1 es una matriz tridiagonal. Si todos los elementos diagonales y todos los elementos a_{i, i ± 1} son distintos de cero, una matriz tridiagonal se denomina "matriz de tipo 2". La inversa de una matriz de covarianza que ocurre en modelos comunes de series de tiempo estacionarias es una matriz de

tipo 2. Usando la notación intuitiva de X y 0 como arriba, una matriz de bandas puede escribirse como

3.1.5 Operadores de conformación de matrices

Para realizar ciertas operaciones en matrices y vectores, a menudo es útil primero remodelar una matriz. La operación de remodelación más común es la transposición, que definimos en líneas atrás. A veces, es posible que necesitemos reorganizar los elementos de una matriz o formar un vector en una matriz especial. 

Transponer

Como se definió anteriormente, la transposición de una matriz es la matriz cuya 

i-ésima fila es la i-ésima columna de la matriz original y cuya j-ésima columna es la 

j-ésima fila de la matriz original. Notamos inmediatamente que

Si los elementos de la matriz son del campo de los números complejos, la transpuesta conjugada, también llamada adjunta, es más útil que la transpuesta.

("Adjoint" también se usa para denotar otro tipo de matriz, por lo que generalmente evitaremos usar ese término. Este significado de la palabra es el origen del otro término para una matriz hermitiana, una "matriz autoadjunta") usa un superíndice "H" para denotar la transposición conjugada de una matriz; así, si A = (aij), entonces

3.1.6 Matrices particionadas

A menudo nos resulta útil dividir una matriz en submatrices; por ejemplo, en muchas aplicaciones de análisis de datos, a menudo es conveniente trabajar con submatrices de varios tipos que representan diferentes subconjuntos de datos.

Usualmente denotamos las submatrices con letras mayúsculas con subíndices que indican las posiciones relativas de las submatrices. Por lo tanto, podemos escribir...

3.1.7 Adición de matrices

La suma de dos matrices de la misma forma es la matriz cuyos elementos son las sumas de los elementos correspondientes de los sumandos. Como en el caso de la suma de vectores, sobrecargamos los símbolos habituales para las operaciones sobre los reales para significar las correspondientes operaciones sobre matrices cuando se definen las operaciones; por tanto, la adición de matrices también se indica mediante “+”, como ocurre con la adición escalar y la adición de vectores. Suponemos que escribir una suma de matrices A + B implica que tienen la misma forma; es decir, que sean aptos para la adición.

El operador "+" también puede significar la adición de un escalar a una matriz, como en A + a, donde A es una matriz y a es un escalar. Aunque este significado de “+” generalmente no se usa en tratamientos matemáticos de matrices, en este curso lo usamos para referirnos a la adición del escalar a cada elemento de la matriz, dando como resultado una matriz de la misma forma. Este significado es consistente con la semántica de los lenguajes informáticos modernos como Fortran y R.

La adición de dos matrices n × m o la adición de un escalar a una matriz n × m requiere adiciones escalares nm.

La identidad aditiva de la matriz es una matriz con todos los elementos cero. A veces denotamos una matriz de este tipo con n filas y m columnas como 0_n×m, o simplemente como 0. Podemos denotar una identidad aditiva cuadrada como 0_n.

3.1.8 Operadores con valores escalares en matrices cuadradas

En la traza hay varias asignaciones útiles de matrices a números reales; es decir, de 

IRn × m a IR. Definimos dos operadores con valores escalares, la traza y el determinante, que se aplican a las matrices cuadradas.

3.1.8.1 La traza: tr (·)

La suma de los elementos diagonales de una matriz cuadrada se llama traza de la matriz. Usamos la notación "tr(A)" para denotar la traza de la matriz A:

3.1.9  El determinante

El determinante, como la traza, es un mapeo de a . Aunque puede que no sea obvio a partir de la definición siguiente, el determinante tiene aplicaciones de gran alcance en la teoría de matrices.

Para una matriz A n×n (cuadrada), considere el producto donde es uno de los n! permutaciones de los números enteros de 1 a n.

Defina que una permutación sea par o impar según el número de veces que un elemento más pequeño sigue a uno más grande en la permutación. Por ejemplo, dada la tupla (1, 2, 3), entonces (1, 3, 2) es una permutación impar y (3, 1, 2) y (1, 2, 3) son permutaciones pares.

El determinante también se escribe a veces como | A |.

Preferimos la notación det (A), debido a la posible confusión entre |A| y el valor absoluto de alguna cantidad.  El determinante de una matriz puede ser negativo y, a veces, como en la medición para volúmenes especiales llamados jacobianos, necesitamos especificar el valor absoluto del determinante, por lo que necesitamos algo de la forma |det (A)|.

La definición del determinante no es tan abrumadora como puede parecer a primera vista. Muchas propiedades se vuelven obvias cuando nos damos cuenta de que la permutación σ(·) es siempre ± 1, y puede construirse mediante intercambios elementales de elementos adyacentes. Por ejemplo, considere σ (3, 2, 1). Hay dos formas en que podemos usar tres intercambios elementales, cada uno comenzando con el orden natural:

 (1,  2,  3) →  (2,  1,  3) →  (2,  3,  1) →  (3,  2,  1),

0

 (1,  2,  3) →  (1,  3,  2) →  (3,  1,  2) →  (3,  2,  1);

por lo tanto, de cualquier manera, σ (3, 2, 1) = (−1) 3 = −1.

Además, vemos que el producto a_1j1 · · · a_njn tiene exactamente un factor de cada par único fila-columna. Estas observaciones facilitan la derivación de varias propiedades del determinante (aunque los detalles a veces son bastante tediosos).

Vemos inmediatamente de la definición que el determinante de una matriz triangular superior o inferior (o una matriz diagonal) es simplemente el producto de los elementos diagonales (porque en cada término de la ecuación (3.24) hay un 0, excepto en el término en que los subíndices de cada factor son los mismos).

Considere la matriz 2 × 2

De la definición del determinante, vemos que

 det(A ) = a11a22 − a12a21

Ahora sea A una matriz de 3 × 3:

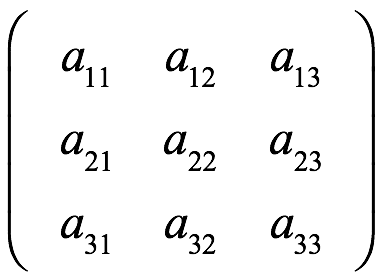
En la definición del determinante, considere todos los términos en los que aparecen los elementos de la primera fila de A. Con alguna manipulación de esos términos, podemos expresar el determinante en términos de determinantes de submatrices como

Ec. 1

 det(A ) = a11 (1)det(a22 ) + a12 (− 1)det(a21 )

La manipulación en la Ec. 1 de los términos del determinante podría realizarse con otras filas de A. Los determinantes de las submatrices 2 × 2 en la Ec. 1 se denominan menores o menores complementarios del elemento asociado. La definición se puede extender a (n − 1) × (n − 1) submatrices de una matriz n × n, para n ≥ 2. Denotamos el menor asociado con el elemento a_ij como

en el que A_{− (i) (j)} denota la submatriz que se forma a partir de A al eliminar la i-ésima fila y la j-ésima columna. El signo asociado con el menor correspondiente a a_ij es . El menor junto con su signo apropiado se denomina cofactor del elemento asociado; es decir, el cofactor de a_ij es det A_{− (i) (j)}. Denotamos el cofactor de a_ij como:

Observe que tanto los determinantes menores como los cofactores son escalares.

Las manipulaciones que conducen a la ecuación 1, aunque algo tediosas, se pueden realizar para una matriz cuadrada de cualquier tamaño mayor que 1 × 1, y los menores y cofactores se definen como antes. Una expresión como la de la Ec. 1 se llama expansión en menores o expansión en cofactores.

La extensión de la expansión Ec. 1 a una expresión que involucra una suma de productos con signo de menores complementarios que surgen de (n - 1) × (n - 1) submatrices de una matriz A de n × n es

Ec. 2

Estas expresiones se denominan expansiones de Laplace. Cada determinante también puede expresarse de forma recursiva en una expansión similar.

Las expresiones Ec. 2  son casos especiales de una expansión de Laplace más general basada en una extensión del concepto de un menor complementario de un elemento al de un menor complementario de un menor. La derivación de la expansión general de Laplace es sencilla pero bastante tediosa.

Las expansiones de Laplace podrían usarse para calcular el determinante, pero el valor principal de estas expansiones es demostrar las propiedades de los determinantes. Por ejemplo, a partir de la expansión especial de Laplace, podemos ver rápidamente que si el determinante de una matriz con dos filas iguales es cero.

Vemos esto al expandir recursivamente todos los menores hasta que solo tengamos matrices de 2 × 2 que consisten en una fila duplicada. El determinante de dicha matriz es 0, por lo que la expansión es 0.

El determinante de la transposición de matrices cuadradas. Una propiedad importante que vemos inmediatamente a partir de una manipulación de la definición del determinante es

El determinante de productos escalares de matrices cuadradas

Para un escalar c y una matriz A n × n,

El determinante de ciertas matrices cuadradas particionadas

Los determinantes de las matrices divididas cuadradas que son diagonales de bloque o triangulares de bloque superior o inferior dependen solo de las particiones diagonales:

El determinante de la suma de matrices cuadradas. De vez en cuando es interesante considerar el determinante de la suma de matrices cuadradas. Observamos en general que

3.1.9.1 Calcular el determinante

Para una matriz arbitraria, el determinante es bastante difícil de calcular. El método para calcular un determinante no es el que surgiría directamente de la definición o incluso de una expansión de Laplace. Los métodos más eficientes implican primero factorizar la matriz… suele ser directamente útil, pero aunque puede que no sea obvio por su definición, el determinante, junto con los menores, cofactores y matrices adjuntas, es muy útil para descubrir y probar las propiedades de las matrices. El determinante se usa ampliamente en autoanálisis.

Una perspectiva geométrica del determinante

La interpretación geométrica útil de vectores en un espacio lineal con un sistema de coordenadas cartesiano. Los elementos de un vector corresponden a medidas a lo largo de los respectivos ejes del sistema de coordenadas. Cuando se trabaja con varios vectores, o con una matriz en la que las columnas (o filas) están asociadas con vectores, podemos designar un vector xi como x_i = (x_i1,..., x_id). Un conjunto de d vectores d linealmente independientes define un paralelogramo en d dimensiones. Por ejemplo, en un espacio bidimensional, los 2 vectores linealmente independientes x₁ y x₂ definen un paralelogramo, como se muestra en la figura.

El área de este paralelogramo es la base multiplicada por la altura, bh, donde, en este caso, b es la longitud del vector x1 y h es la longitud de x2 multiplicada por el seno del ángulo θ. Por lo tanto, utilizando la ecuación (2.54) de la página 37 para el coseno del ángulo, tenemos

Donde 

 x1 = ( x11 , x12),  x2 = ( x21 , x22),

Y

Aunque aquí no pasaremos por los detalles, se extiende esta equivalencia de un volumen de un paraleloótopo que tiene un vértice en el origen y el valor absoluto del determinante de una matriz cuadrada cuyas columnas corresponden a los vectores que forman los lados del paraleloótopo a dimensiones superiores.

Usamos el valor absoluto del determinante del jacobiano como un elemento de volumen. Otro ejemplo de la interpretación del determinante como volumen es la varianza generalizada.

3.1.9.2 Matriz inversa por la matriz adjunta

La inversa de una matriz cuadrada A, a veces llamada matriz recíproca, es una matriz tal que

donde I es la matriz de identidad. Una matriz cuadrada A tiene una inversa si el determinante . El llamado teorema de la matriz invertible es un resultado importante en el álgebra lineal que asocia la existencia de una matriz inversa con una serie de otras propiedades equivalentes. Una matriz que posee una inversa se llama no singular o invertible.

La matriz inversa de una matriz cuadrada A. Para una matriz de 2 × 2

La matriz es invertible si

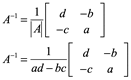
Para una matriz 3x3 o mayor se suele usar la matriz adjunta, que es la matriz de transpuesta de la matriz de cofactores de A.  

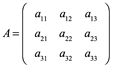
Su matriz de cofactores está dada por(cada submatriz se construye cancelando renglones y columna de cada Cofactor de A_{ij  y signo es dado por (-1)}i+j

:

Propiedades de la matriz inversa

Una matriz general n × n se puede invertirse utilizando otros métodos como la eliminación de Gauss-Jordan, la eliminación de Gauss o la descomposición de LU.

Ejemplo 1: Calcule la inversa por la matriz adjunta, dada la matriz A

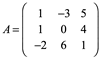
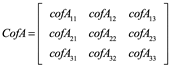
Calculamos cada cofactor de A:

Entonces la matriz de cofactores es:

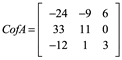
Se calcula el determinante de A

Det A=33

Finalmente con la traspuesta de cof A^T 

Comprobar multiplicando

3.2 Multiplicación de matrices y multiplicación de vectores y matrices

Los elementos de un vector o matriz son elementos de un campo, y la mayoría de las operaciones matriciales y vectoriales se definen en términos de las dos operaciones del campo. Por supuesto, en este libro, el campo de mayor interés es el campo de los números reales.

3.2.1 Multiplicación de matrices (Cayley)

Hay varios tipos de multiplicación de matrices que pueden resultar útiles. El tipo más común de multiplicación es la multiplicación de Cayley. Si el número de columnas de la matriz A, con elementos a_ij, y el número de filas de la matriz B, con elementos b_ij, son iguales, entonces el producto (Cayley) de A y B se define como la matriz C con elementos:

Este es el tipo más común de producto matricial, y nos referimos a él con la frase no calificada "multiplicación de matrices".

La multiplicación de la matriz de Cayley se indica por yuxtaposición, sin símbolo intermedio para la operación: C = AB.

Si la matriz A es n × m y la matriz B es m × p, el producto C = AB es n × p:

La multiplicación de matrices de Cayley es un mapeo,

La multiplicación de una matriz n × m y una matriz m × p requiere multiplicaciones escalares nmp y adiciones escalares np(m - 1). Aquí, como siempre en el análisis numérico, debemos recordar que la definición de una operación, como la multiplicación de matrices, no necesariamente define un buen algoritmo para evaluar la operación.

Es obvio que si bien el producto AB puede estar bien definido, el producto BA se define solo si n = p; es decir, si las matrices AB y BA son cuadradas.

Suponemos que escribir un producto de matrices AB implica que el número de columnas de la primera matriz es el mismo que el número de filas de la segunda; es decir, se pueden multiplicar en el orden dado.

Es fácil ver en la definición de multiplicación de matrices que en general, incluso para matrices cuadradas, AB = BA. También es obvio que si AB existe, entonces existe:

Debido a que la multiplicación de matrices no es conmutativa, a menudo usamos los términos "premultiplicar" y "postmultiplicar" y las formas nominales correspondientes de estos términos. Por lo tanto, en el producto AB, podemos decir que B es premultiplicado por A o, de manera equivalente, A es posmultiplicado por B.

Aunque la multiplicación de matrices no es conmutativa, es asociativa; es decir, si las matrices son conformables,

A (BC) = (AB) C.

También es distributiva sobre la suma; es decir,

A (B + C) = AB + AC 

y

(B + C) A = BA + CA. 

Estas propiedades son obvias a partir de la definición de multiplicación de matrices.

(Tenga en cuenta que la distribución del lado izquierdo no es lo mismo que la distribución del lado derecho porque la multiplicación no es conmutativa).

Una matriz n×n que consta de unos a lo largo de la diagonal y ceros en cualquier otro lugar es una identidad multiplicativa para el conjunto de matrices n×n y la multiplicación de Cayley. Tal matriz se llama matriz identidad de orden n, y se denota por I_n, o simplemente por I. Las columnas de la matriz identidad son vectores unitarios.

La matriz de identidad es una identidad multiplicativa para cualquier matriz siempre que las matrices sean conformes para la multiplicación. Si A es n × m, entonces

Otra matriz de interés es una matriz cero o matriz nula, que es cualquier matriz que consta de todos ceros. Denotamos una matriz cero como 0, con su forma implícita en el contexto. Dos propiedades para cualquier matriz A y una matriz cero de la forma apropiada son inmediatamente obvias:

 0A  = 0

y 

0 + A  = A.

Multiplicación de matrices particionadas. La multiplicación y otras operaciones con matrices particionadas se realizan con sus submatrices de la forma obvia. Por lo tanto, asumiendo que las submatrices son compatibles con la multiplicación,

Está claro que el producto de las matrices diagonales de bloques conformables es la diagonal de bloques.

3.2.2 Operaciones elementales en matrices

Muchos cálculos comunes que involucran matrices se pueden realizar como una secuencia de tres tipos simples de operaciones en las filas o columnas de la matriz:

• el intercambio de dos filas (columnas),

• una multiplicación escalar de una fila (columna) dada, y

• el reemplazo de una fila (columna) dada por la suma de esa fila (columnas)

y un múltiplo escalar de otra fila (columna); es decir, una operación axpy.

Una operación de este tipo en las filas de una matriz se puede realizar mediante la premultiplicación mediante una matriz en una forma estándar, y una operación en las columnas de una matriz se puede realizar mediante una multiplicación posterior mediante una matriz en una forma estándar. Repetir:

• premultiplicación: operación en filas;

• posmultiplicación: operación en columnas.

La matriz utilizada para realizar la operación se denomina matriz de transformación elemental o matriz de operador elemental. Tal matriz es la matriz de identidad transformada por la operación correspondiente realizada en sus filas unitarias, , o columnas, e_p.

En los cálculos reales, no formamos las matrices de transformación elementales explícitamente, pero su formulación nos permite discutir las operaciones de una manera sistemática y comprender mejor las propiedades de las operaciones.

Los productos de cualquiera de estas matrices de operadores elementales se pueden utilizar para efectuar transformaciones más complicadas.

Las operaciones en las filas son más comunes, y eso es lo que discutiremos aquí, aunque las operaciones en las columnas son completamente análogas. Estas transformaciones de filas se denominan operaciones de fila elementales.

Intercambio de filas o columnas: matrices de permutación

Intercambiando primero las filas o columnas de una matriz, puede ser posible dividir la matriz de tal manera que las particiones tengan propiedades interesantes o deseables. Además, en el transcurso de realizar cálculos en una matriz, a menudo es deseable intercambiar las filas o columnas de la matriz. (Este es un caso de “pivotar”, que se discutirá más adelante) En los cálculos matriciales, casi nunca movemos datos de una fila o columna a otra; más bien, los intercambios se efectúan cambiando los índices a los datos. El intercambio de dos filas de una matriz se puede lograr multiplicando previamente la matriz por una matriz que es la identidad con esas mismas dos filas intercambiadas; por ejemplo,

La primera matriz de la expresión anterior se llama matriz de permutación elemental. Es la matriz de identidad con su segunda y tercera filas (o columnas) intercambiadas. Una matriz de permutación elemental, que es la identidad con las filas p^th y q^th intercambiadas, se denota por E_pq. Es decir, E_pq es la identidad, excepto que la p-ésima fila es y la q-ésima es . Tenga en cuenta que E_pq = E_qp.

Así, por ejemplo, si la matriz dada es 4 × m, para intercambiar la segunda y tercera filas, usamos

Es fácil ver por la definición que una matriz de permutación elemental es simétrica. Tenga en cuenta que la notación E_pq no indica el orden de la matriz de permutación elemental; que debe especificarse en el contexto.

Multiplicar previamente una matriz A por un E_pq (conforme) da como resultado un intercambio de las filas p^th y q^th de A como vemos arriba. Cualquier permutación de filas de A puede lograrse mediante premultiplicaciones sucesivas mediante matrices de permutación elementales. Tenga en cuenta que el orden de la multiplicación es importante. Aunque una determinada permutación puede lograrse mediante diferentes permutaciones elementales, el número de permutaciones elementales que efectúan una determinada permutación es siempre par o impar; es decir, si un número impar de permutaciones elementales da como resultado una permutación dada, cualquier otra secuencia de permutaciones elementales para producir la permutación dada también es impar en número. Cualquier permutación dada puede efectuarse mediante intercambios sucesivos de filas adyacentes. Postmultiplicar una matriz A por un E_pq (conforme) da como resultado un intercambio de las columnas p^th y q^th de A:

Tenga en cuenta que

es decir, como operador, una matriz de permutación elemental es su propio operador inverso:

Debido a que todos los elementos de una matriz de permutación son 0 o 1, la traza de una matriz de permutación elemental n×n es n-2.

El producto de las matrices de permutación elementales es también una matriz de permutación en el sentido de que permuta varias filas o columnas.

Una matriz de permutación general (es decir, un producto de matrices de permutación elementales) no es necesariamente simétrica, pero su transposición es también una matriz de permutación. No es necesariamente su propia inversa, pero sus permutaciones pueden invertirse mediante una matriz de permutación formada por productos de matrices de permutación en el orden opuesto; es decir,

Transformaciones de fila o columna de axpy. La otra operación elemental es un axpy en dos filas y un reemplazo de una de esas filas con el resultado

Esta operación también se puede efectuar por premultiplicación mediante una matriz formada a partir de la matriz identidad insertando el escalar en la posición (p, q). Esta matriz se denota por E_pq(a). Así, por ejemplo, si la matriz dada es 4×m, para sumar a veces la tercera fila a la segunda fila, usamos

Premultiplicación de una matriz A por dicha matriz,

produce una matriz cuya p-ésima fila es a multiplicada por la quinta fila más la fila original. Dada la matriz A  de 4 × 3 = (a_ij), tenemos

Postmultiplicación de una matriz A por una matriz de operador axpy,

produce una matriz cuya quinta columna es a multiplicada por la pésima columna más la columna original. Para esto, E_pq(a) es una matriz cuadrada de orden igual al número de columnas de la matriz dada. Tenga en cuenta que la columna que se cambia corresponde al segundo subíndice en E_pq (a).

Tenga en cuenta que

es decir, como operador, el operador inverso es la misma matriz de operador elemental axpy con el negativo del multiplicador.

Un uso común de las matrices de operadores axpy es formar una matriz con ceros en todas las posiciones de una columna dada debajo de una posición dada en la columna. Estas operaciones suelen seguir una operación mediante una matriz multiplicadora de filas escalar que coloca un 1 en la posición de interés. Por ejemplo, dada una matriz A de n×m con a_ij = 0, para poner un 1 en la posición (i, j) y ceros en todas las posiciones de la j-ésima columna debajo de la i-ésima fila, formamos el producto

Este proceso se llama eliminación gaussiana.

La matriz

se llama matriz de transformación gaussiana. Observe que es triangular inferior, y su inverso, también triangular inferior, es

La eliminación gaussiana se realiza a menudo de forma secuencial por los elementos diagonales de una matriz.

Ejemplo 2: Calcule la matriz inversa por eliminación gaussiana

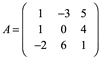
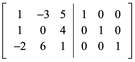
Restar renglón 1 al renglón 2 o Restar -R1+R2

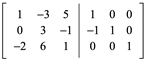
Sumar 2(R1) a R3

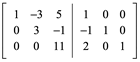
Dividir R3 por 1/11

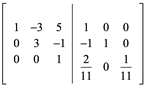
Sumar R3 a R2

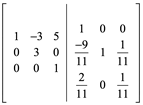
Multiplicar 5R3 y restar el resultado a R1

Dividir R3/3

3xR2 y sumar R1

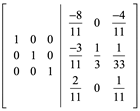
El resultado es idéntico al realizado por el método de la Adjunta:

__________________________________________________

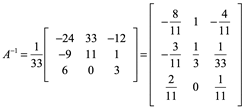
Autores:

Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Lizbeth Guadalupe Villalon Magallan
Mónica Rico Reyes
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán