Texto universitario

_____________________________

Módulo 5. Continuidad y límites 

Una idea común de continuidad es que una función es continua “si puedes dibujarla sin quitar tu pluma de la página”. Esto no es malo como una primera aproximación, para muchas funciones simples conducirá a conclusiones correctas. Pero es fácticamente limitada en un sentido bastante trivial y, operativamente limitada de una manera más seria. Es limitado de hecho porque un gráfico puede mostrar solo una parte finita de una función de los reales a los reales; a menudo dibujada con el bit alrededor del origen (0,0). Así que lo que la gente realmente quiere decir es que creen que todo el gráfico sería  “en una solo pieza conectada”. El problema más grave es que aunque la descripción del dibujo suena práctica porque se trata de una acción física, no se puede utilizar en el razonamiento matemático. 

Un primer paso sensato hacia la definición matemática, es dejar la continuidad como una propiedad de un todo en la función y, empezar a pensar en ella como una propiedad que podría tener en un punto. Casi con toda seguridad ya lo hace, si definimos una función por partes no lo consideramos continua en 1, ¿pero es continua en todas partes?

Los matemáticos toman esto como un lugar para comenzar, definen lo que  significa que una función sea continua en un punto y solo entonces hablan de funciones que son continuas en todas partes. Ya en esta instancia la mayoría de los estudiantes han trabajado con funciones estándar, como la cuadrática, cúbica, polinomial de orden superior, racionales, exponenciales, logarítmicas, trigonométricas. En el análisis matemático en general las personas se ocupan de los dominios de la función. Esto es por la necesidad adecuada de especificar estos objetos matemáticos. Se identifica que hay funciones, por ejemplo que no son continuas en cero y se definan en el resto en todos los reales. Los estudiantes cuidan el rango o imagen de una función, considerándolo el conjunto de valores que realmente obtienen salida de una función. Y al dominio como los valores que la función asigna. 

Siempre que denotamos un intervalo que se extiende hasta el infinito usamos , el paréntesis se emplea para expresar un intervalo abierto, porque no es un número, mucho menos un número muy grande o un intervalo. Cuando trabajamos funciones por piezas en intervalos, pero que es solo una función que asigna solo un valor único. Incluso podemos construir funciones que asignan un número aleatorio. Por supuesto son difíciles de trabajar. Pero a un teorema no le importan los detalles de una función siempre que se aplique sus premisas, y una función no tiene que especificar mediante una única fórmula simple, o incluso mediante una fórmula en absoluto. Podemos emplear funciones por piezas son ellas en esos intervalos son continuas. Otras funciones no satisfacen esta propiedad. 

Los números racionales e irracionales se distribuyen de una manera complicada en la línea numérica, sea cual sea el número racional que se escoja, hay irracionales tan cercanos dentro de intervalos y esta función no es continua en esos valores, es imposible dibujar su gráfico de una manera realista. Tenga presente que la continuidad es definida por los matemáticos en un punto. Supongamos que f(a) es continua donde toma el valor a. ¿Cómo podríamos capturar esta idea? Podemos decir, a medida que x se acerca a un a, f(x) se acerca a a. Este es un comienzo sensato, pero no es suficiente, que podemos ver mirando las Imag5 que muestra una función que es continua en un a y en uno que no lo es. En ambos casos es cierto que a medida que x se acerca a a, f(x) se acerca f(a). Es solo que no es un acercamiento lo suficientemente preciso. 

Una función f es continua para a sí y solo si, haciendo x lo suficientemente cerca de a, podemos hacerlo f(x) cerca muy cerca de f(a). Para convertir la descripción informal en una más formal, necesitamos obtener una idea algebraica sobre la idea de cerrar. Supongamos que queremos f(x) estar a poca distancia de f(a). Se denota epsilon letra griega. Así que queremos o en forma más abreviada

En este contexto podemos leer como la distancia entre f(x) y f(a) es menos que . Ahora, toda la descripción dice …haciendo x los suficientemente cerca de a, podemos f(x) hacerlo siempre más cerca f(a)… para capturar esta idea los matemáticos escriben la siguiente letra griega delta . 

Considere leer esta expresión en voz alta y piense en cómo se relaciona cada parte con el dibujo. Piense en ello así, la repuesta que buscamos es la distancia más pequeña que incluiría algunos valores de x a la izquierda de a para el cual:

Todo esto es solo para un valor de , sin embargo. Si imaginamos un pequeño, esto captura la noción que podemos hacer acercar f(x) cerca de f(a). Pero no captura la idea de que podemos hacerlo lo más cerca que queremos. Para eso, ayuda que imaginemos cada vez más pequeño; necesitamos que sea cierto que para que podamos obligar f(x) a estar a una distancia de f(a) haciendo x lo suficientemente cerca de a. Esto conduce a la definición:

Una función es continua para sí y solo si

Si ya ha iniciado un curso de análisis, es posible que haya visto esta definición expresada de forma ligeramente más diferente, o que haya visto una variante que implique una función límite o quizá, expresada en secuencias infinitas. 

Esta definición se trata de que f sea continua en a, donde a se trata como un punto de interés fijo. La definición también implica un punto general x y su valor f(x) asociado. Esta notación es bastante estándar, los matemáticos a menudo usan letras del principio del alfabeto para cosas contantes y letras del final para cosas variables. Esta definición es de convergencia de secuencias. 

Para ver la importancia de esto, tenga en cuenta que puede que no exista un apropiado para la función que no es continua en a. 

¿Y el resto del bit?

Esto refiera a los epsilon mayores que cero, lo que ya sabemos es cierto. Para la función continua, podríamos imaginar permitir varíe, para valores más pequeños de pero tales valores todavía existirían. 

En general hemos capturado la idea informal y formal pensando en la definición, el diagrama y la interpretación de:

Una función es continua para sí y solo si

La continuidad está estrechamente relacionada con los límites. Las dos funciones que se muestran a continuación son discontinuas en a. Pero son discontinuas de maneras cualitativamente diferentes. La primera no tiene un límite como x tiende a a: puntos a la izquierda y a la derecha de a tienen valores de función que están lejos entre sí. La segunda función tiene un límite como x tiende a a: si imaginamos acercarse por un lado, los valores de la función se acercan al números l, y los matemáticos dirían que tiende a l como x ende a a. Sucede que, por lo que la función no es continua en a, pero tiene un límite. 

Esto, en nuestra opinión, proporciona la visión clave de la relación entre los límites y la continuidad, explica una variante de la definición de continuidad: 

Una función es continua para sí y solo si existe y es igual para f(a).

En efecto, la continuidad requiere que exista el límite y que el valor esté en el lugar correcto. Esa es la intuición o al menos la versión de la misma que tiene sentido para nosotros, cuidado con otras explicaciones si no estás del todo satisfecho. Las definiciones de límite y continuidad aparecen a continuación para que pueda compararlas.

Definición de límite 

sí y solo si 

Definición de continuidad

Una función es continua para sí y solo si

La definición de límite implica un límite general l en lugar del valor f(a). La única otra diferencia es que para los límites requerimos que algo se mantenga si en lugar de .¿Qué efecto tiene esto? Pensar en términos de distancias, significa que la distancia entre x y a es estrictamente mayor que cero, por lo que y la definición no dice nada sobre lo que sucede en el punto x=a. Por lo tanto, una función puede tener un límite en a sin tener el valor correcto f(a). De hecho, puede tener un límite incluso si f(a) no está definido.

La versión límite de la definición de continuidad proporciona una forma sencilla de pensar sobre algunas de las funciones citadas anteriormente. De las siguientes funciones, por ejemplo, solo la izquierda no es continua en cero. Las demás son continuas en cero porque, aunque se definen de manera diferente a la izquierda y a la derecha de cero, cada uno tiene el mismo límite desde la izquierda y desde la derecha, este limite es igual a f(0). 

  Lo que se requiere para probar esto puede depender del enfoque de su curso. En cursos de bachillerato a menudo es suficiente simplemente observar que los límites de la izquierda y de la derecha son los mismos o diferentes. En el análisis, es probable que se espera que pruebe cualquier reclamo de este tipo a partir de la definición de límite. Debido a que las definiciones de límite y continuidad tienen estructuras similares, la información ya discutida debería ser útil para pensar cómo diferenciar esto. 

La continuidad es un tema sustancialmente complejo de su definición central. Ya que hemos hecho algo de trabajo en continuidad, ahora pasaremos a la diferenciación, tiende a ser más fácil que la continuidad. Pero se necesita un tema puente, el teorema de valor extremo:

Supongamos que es continuo sobre [a,b] entonces

1. f está limitada a [a,b]

2. de tal manera que

Esto se afirma a menudo más brevemente como una función continua en un intervalo cerrado que está limitada y alcanza sus límites, ¿puede ver por qué? Y bueno realice una práctica para comprensión del teorema. Dibuje algunos diagramas y pregúntese por qué tiene que ser cierto, luego intente dejar caer una de las premisas, ¿la conclusión seguiría siendo si la función no tuviera que ser continua? ¿Qué pasaría si se definiera en un intervalo abierto en lugar de un un intervalo cerrado? ¿Y por qué cree que esto se llama el Teorema de valor extremo? Un intervalo cerrado es un ejemplo de la noción más general de un conjunto compacto. 

5.1 ¿Qué es la diferenciabilidad? 

No sobre qué es diferenciación. Probablemente ha estado estudiando la diferenciación durante un año y nada sube su capacidad para diferenciar funciones estándar usando fórmulas. Estamos más interesados en lo que realmente significa que una función sea diferenciable. Es posible que hayas pensado esto, pero luego lo olvidaste porque no estaba en un examen, o tal vez nunca lo hayas pensado, tal vez acabas aprender diferenciar usando tablas de derivadas. Cualquiera que sea el caso, uno de los objetivos es fortalecer su conocimiento de formas intuitivas y formales de pensar en la diferenciabilidad y asegurarse de que usted tiene un buen sentido de esos vínculos entre las dos. 

En una primera aproximación, una función es diferenciable en un punto si tiene sentido hablar de ella como que tiene un cierto gradiente o pendiente en ese punto. Equivalentemente una función es diferenciable en un punto si tiene sentido colocar una línea tangente en el gráfico en ese punto. Consideremos, por ejemplo, una función lineal dada por . Esta función gradiente 3 en todas partes. Probablemente no has pensado mucho en las líneas tangentes para las funciones lineales, porque las tenientes son realmente solo interesantes cuando un gráfico es curvilíneo en lugar de recto. Pero la tangente a este gráfico lineal es la misma que el gráfico en sí, para ver cómo funciona algebraicamente, elija un punto y siga su enfoque habitual para encontrar líneas tangentes. Ciertamente tiene sentido haber de gradientes para funciones como esta. 

A continuación, considere una función no lineal, por ejemplo dada por . Claramente la noción de gradiente que se aplica a las funciones de este tipo dadas por el formulario no es y=mx+b. El gráfico es curvo, pero si imaginamos hacer zoom una y otra vez, lo que vemos se parece cada vez más a una línea recta del polígono regular de n números de lados. En realidad nunca es una línea recta, pero para la mayoría de la gente estaría feliz de decir que en el límite, es posible poner una línea tangente sensible en el gráfico: estaríamos satisfechos de que esta línea coincide con la función en un punto en el sentido de que su valor es el mismo y su gradiente es el mismo. 

Por lo tanto, para una función como , el gráfico es curvo, pero tiene sentido intuitivo hablar de degradados. No podemos hablar del gradiente del gráfico, como podemos para , porque el degradado sigue cambiando. Pero podemos hablar del gradiente en un punto, que es lo suficientemente bueno. 

Sin embargo, no todas las funciones son así.  Considere, por ejemplo, la función dada por . En la mayoría de los puntos, esto tiene un gradiente sensible: a la izquierda de 0,m el gradiente es -1; a la derecha es 1. Pero ¿qué pasa en el punto? ¿Qué pasa si nos acercamos allí? Algo diferente, podemos acercarnos todo lo que queramos y el gráfico nunca se ve más recto. Siempre tiene una esquina  ni menos puntiaguda. Así que no tiene sentido decir que el gráfico tiene un gradiente en cero y no podemos dibujar una línea tangente que “coincide” con el gráfico. 

De esto se trata la diferenciabilidad. Informalmente, una función es diferenciable en un punto si tiene sentido especificar un gradiente en ese punto y, por lo tanto, pensar en una línea tangente significativa en ese punto. Una función no es diferenciable en un punto si tiene una esquina allí. 

Una función no es diferenciable en un punto si tiene una esquina allí. Esto glosa muchos detalles técnicos y consideraciones más sofisticadas, pero queremos que piense en la diferenciabilidad como un concepto significativo y este es un lugar decente para empezar.

Antes de ver la definición formal de diferenciabilidad, queremos llamar su atención sobre algunos conceptos erróneos comunes sobre derivadas y líneas tangentes. En primer lugar, frente a un punto en un gráfico para el que no hay un línea tangente significativa, las personas a veces se sienten tentadas a poner una de todos modos. En una esquina, pueden dibujar una “tangente” que está a mitad de camino entre las tangentes de ambos lados o incluso dibujar varias “tangentes” a ambos lados como si giran alrededor del punto a medida que se mueve de una parte a otra del gráfico. 

En relación a la teoría matemática de la geometría de polígonos regulares infinitos, esto está mal. En cualquier momento, un gráfico tiene un único gradiente significativo y por lo tanto, una línea tangente significativa o no. No hay ningún problema con trabajar con bocetos gráficos de funciones, pero debemos asegurarnos de que nuestra interpretación de un gráfico esté informada por la naturaleza de la función, en lugar de permitir que la intuición sobre la función se invoque mediante un gráfico engañoso a la ligera. 

Algunos estudiantes se encuentran primero con tangentes no en relaciones con las funciones, sino en relación con los círculos. Una tangente a un círculo se encuentra con el círculo en un solo punto y no cruza el círculo, es decir, en ambas direcciones es hacia fuera de este. Eso es obvio cuando se mira una imagen:

Ninguna de estas cosas se mantiene para que las rectas tangentes funcionen  así. Es perfectamente posible que una tangente se encuentre con el gráfico en más de un punto, y que cruce el gráfico en el punto de tangencia o en algún otro punto. Por ejemplo, considere de nuevo la función  dada por . ¿Puede identificar puntos en los que la tangente cruza la curva en el punto de tangencia?  Probablemente nadie generaliza explícitamente círculos en gráficos de funciones: ningún estudiante tiene una idea en principio que círculos y funciones son lo mismo, por lo que la tangente no debe cruzar el gráfico. Pero es importante recordar que la comprensión acumulada en un área de las matemáticas podría no aplicarse en otra. Una curva está hecha de para los lados de un círculo, y una curva es para cada punto de ella, el lado de un círculo. 

La mayoría no tiene ningún problema en declarar que la derivada de una función es cero en x=0. Sin embargo, bastantes se confunden cuando comenzamos a hablar de derivadas de dada por g(x)=5. Algunos no están muy seguros de que realmente sea una función. Después de todo, 5 es solo un número, y seguramente pensarían que una función debería tener una x en ella. Un vez más, probablemente nadie piensa explícitamente esto, pero la gente se siente perturbada a veces se aclara con una mejor escritura que lo explique. Si escribimos la función dada por g(x)=5 donde cada , parece un poco mejor. Otros piensan que no se puede diferenciar un número, esto es técnicamente cierto, pero no en la forma en que lo dicen. No podemos diferenciar un número, no es el tipo correcto de objeto, pero podemos diferenciar una función que en todas sus partes tomo ese número como su valor, como en el caso de g(x)=5. La derivada de g es cero en todas sus partes porque g es una función constante por lo que su gráfico es plano. Una derivada es un operador que transforma una función en otra función que nos genera los ángulos de inclinación de las rectas tangentes a la curva en cualquier punto. 

Sabemos que una constante se diferencia de cero, son simplemente funciones constantes. Aquí cero no es nada o vacío, es un ángulo de inclinación. Incluso cuando se mira un gráfico de una función constante, por error muchos consideran que no tiene derivada, mal interpretando tener derivada cero con no existe la derivada. Es fácil ver de dónde viene esto, primero aprendemos sobre los números contando objetos del mundo y, tener cero de algo es lo mismo que no tener nada. Pero matemáticamente cero no es nada, es un número perfectamente bueno. Si usted está dispuesto a decir que la derivada es cero, no se refiere a nada, sino a algo, como un ángulo cero. 

El número cero aparece como idea justo después de que el hombre consolida los números enteros positivos, antes que aprendiera a escribir y leer. El cero llegó como algo paradójico relacionado con la nada y misterioso cuando la sociedad se preguntó ¿cómo puede existir un número para la nada? Desde el punto de vista abstracto, el cero es muy sencillo, solo es un apoyo para los sistemas de numeración con las siguientes propiedades.

0 es la identidad para la adición: 0 + a =a, para un número cualquiera a. No es todo lo que debemos saber de cero, visto como la identidad bajo la suma. Cómo demostrar que 0x3=0, donde 3 se define como 1+1+1. En primer lugar, la ley conmutativa de la multiplicación: ab=ba, para cualquiera dos números a y b. no dice que 0x3=3x0. A continuación, la ley distributiva: (a+b)c=ac+bc,  para cualesquier tres números a,b,c, nos dice que (1+1+1)x0=1x0+1x0+1x0. Pero 1x0=0 mediante 1 es en la multiplicación la identidad: 1a=a para un número a, así que esto es igual a 0 + 0. Y por la regla 0 es un la identidad para la adición: 0 + a =a, para un número cualquiera a, implica que 0+0=0, y la argumentación termina.

S1) La ley conmutativa para la adición: a + b= b + a, para cualquiera dos números a y b.

S2) La Ley asociativa de la adición: a + (b + a )= (b + a) +c, para tres números cualquier a,b,c.

S3) 0 es un la identidad para la adición: 0 + a =a, para un número cualquiera a.

M1) Ley conmutativa de la multiplicación: ab=ba, para cualquiera dos números a y b.

M2) La Ley asociativa de la multiplicación: a(bc)=(ab)c, para tres números cualquiera  a,b,c.

M3) 1 es en la multiplicación la identidad: 1a=a para un número a.

D1) La ley distributiva: (a+b)c=ac+bc, para cualesquier tres números a,b,c.

Un argumento no abstracto sería decir que 0x3 significa no sumar 3 y así nos quedamos con cero. Pero esta forma hace que el pensamiento no sea riguroso para contestar por ejemplo ¿por qué cero veces cero es cero, puesto que cero veces no representa la nada? 

0=1x0   por la regla M3

0=(0+1)x0 por la regla S3

0=0x0+1x0 por la regla D1

0=0x0+0 por la regla S1

0=0x0 por la regla S3

Estamos dando este camino de demostración, porque nos parece que las demostraciones matemáticas son interesantes para desarrollar el pensamiento, y además por el deseo de mostrar lo que significa justificar las declaraciones aritméticas abstractas, empleando reglas simples sin preocuparnos de lo que realmente es el número cero. Por supuesto que es necesario asociar el significado de un número con Imag5 mentales de los objetos matemáticos, a menudo estas asociaciones porcentuales no son suficientes para decirnos qué hacer en contextos nuevos y desconocidos. Entonces el método abstracto se convierte en indispensable.

El concepto de cero no solo es misterioso por evocar a la nada, un vacío primordial, además, resulta de un peligro real, dado que con el cero existe la posibilidad de romper el marco de la lógica. Hemos dicho que el cero nace después de los números enteros positivos, dado que la hipótesis que sostenemos, afirma que los hombres necesitaron primero registrar todo lo existente, como animales y otras cosas; y así durante algún tiempo al hombre no se le presentó más necesidad de contar y registrar. Cero resultó tan extraño que algunas culturas nunca lo demandaron, les resultó absurdo contar la nada. Los primeros registros que se conocen de los números fueron sobre tablas de arcilla y huesos de lobo. Pero en ellos hay evidencia que el hombre solo pensó la unidad y una serie creciente positiva de muchos números más. La base numérica de base 10, se cree es un accidente a través de las culturas que tomaron la cantidad de los dedos de las manos como el número de símbolos base para contar. Los griegos emplearon la palabra "oscuro" para referir el proceso de recuento. Otras culturas emplearon el sistema de base 5, o quinario; los Mayas emplearon la base 20 por corresponder a la cuenta de dedos de pies y manos, parece que las culturas antiguas  gustaron de emplear al cuerpo humano como referencia para contar. 

Hemos argumentado que contar cero caballos o cero niños pudiera parecer que no es necesario, un número para contar algo que representa la ausencia de ese objeto. Quizá por ello muchas culturas siguieron con sistemas sin incluir el cero. Las personas que podían llevar la cuenta del tiempo, del espacio, de cosechas, eran considerados dioses, sacerdotes y su rango social era una jerarquía muy cercana a jerarcas, emprendedores y líderes. Pero para evitar hacer del conteo un recital apoyado en el número de dedos, se hace necesario un sistema numérico simbólico para registros complejos. Se sabe que las cifras de conteo se crean mucho antes que la escritura y la lectura tempranas en la civilización. Las piedras, huesos y arcillas labradas anteceden a las tintas. Transcribir el sistema oral ha escrito, fue un sistema de descodificación por el que escribas podían fijar los números en primer lugar, antes que las narrativas de la condición humana. 

Lo primero fue resolver un sistema base que hiciera pensar a los números como contenedores de la noción de cantidad, en lugar de marcas, se emplean símbolos para cada agrupación base, donde cada uno de ellos pudiera ser reciclado para expresar series más complejas. Fueron los Egipcios los que desarrollaron un sistema decimal hace más de 5000 años, donde cuadros estaban separados para recibir números, con una sola marca vertical se representaba la unidad. Para escribir 135 con este sistema, en lugar de emplear 135 marcas para esa misma cantidad de unidades, los egipcios escribían seis símbolos: una trampa, tres talones y cinco marcas verticales. Fue la manera típica de hacer matemáticas en la antigüedad, y como muchas otras civilizaciones no emplearon el cero para contar, aunque en su geometría lo emplearon para referir al origen de todo sistema geométrico.

Los griegos también conocieron la unidad, a partir de ella mediante un sistema decimal desarrollaron una serie de números positivos crecientes, pero en este caso cuando la unidad era dividida 1/10, 1/100, 1/1000, 1/10000, 1/n = átomo. El átomo fue resultado de dividir una unidad de roca, donde el límite era un átomo o parte indivisible de la materia. Aquí es de destacar que la nada y la realidad material tenían como frontera los átomos. Donde n representaba al número de lados de un círculo, es decir, un círculo es un polígono regular,  mismos ángulos interiores y longitudes de lado para un polígono que se le aumenta indefinidamente en número hasta llegar al átomo. Y al igual que los Egipcios no necesitaron del número cero.

La necesidad de contar con un calendario, una vez que la conciencia humana alcanzó certeza sobre ciclos de repetición en cambios lunares y climáticos relacionados con la inclinación de los ángulos de la luz solar, es que el hombre perfecciona los sistemas numéricos para cuentas más precisas y complejas. El mes lunar se calculó entre 29 y 39 días, que son 12 meses lunares de 354 días,  11 días por debajo del calendario solar pensado por los Mayas. Corregir el año lunar es una tarea compleja, pero necesaria para empatar con precisión las estaciones del año. También los Egipcios emplearon el año solar para ello; sobre un sistema numérico de base 10, para la semana llamada década fue de 10 días, que suman en un año 365 días. Este calendario fue adoptado por los griegos y luego por el imperio romano, este último modificó la adición de años bisiestos y entonces se convirtió en el calendario occidental sin ceros en su estructura, un problema que podría causar sesgos de milenios más tarde. La innovación Egipcia del calendario no fue la mayor aportación a la civilización occidental, sino el arte de la invención de la geometría. Incluso sin un cero, los egipcios habían representado el origen geométrico como un lugar sin dimensiones. La geometría nace por la necesidad de tomar muy en serio el respeto a la propiedad de áreas de cultivo. Las parcelas se dividieron en rectángulos y triángulos buscando ser lo más preciso posible. La geometría plana egipcia evoluciona al espacio tridimensional para calcular volúmenes de materia en la arquitectura. Así que el punto de origen geométrico sin expresarlo así, fue el cero egipcio para referir un lugar de referencia sin dimensiones y a partir de este medir el espacio circundante.

Los griegos a diferencia de los Egipcios, incluyen en las matemáticas el pensamiento filosófico. Es extraño que los griegos no descubrieran al cero, pero mejoraron el sistema decimal incorporando letras en lugar de iconos y el sistema de base 10 se hace más sofisticado. Pero no aparece cero en su cultura, es en el actual Irak que los babilonios introducen el cero en el sistema numérico sexagecimal, es decir, de base 60 para sus símbolos básicos. En lugar de emplear nuevos símbolos para diferentes números, era posible hacerlo solo con los básicos. Esto les permite a los babilonios crear las primeras máquinas en ayuda a las cuentas, aunque fueron los chinos y su ábaco la primer máquina de contar conocida. Los babilonios crean las palabras calcular y cálculo precursoras de la informática moderna. El sistema babilonio es posicional, muy parecido al ábaco en este sentido. Cada agrupación tiene un valor diferente dependiendo de su posición. De esta manera, el sistema babilonio no era tan diferente al que hoy usamos. Posiciones de unidad, de derecha a izquierda para referir 1, 10,100,1000,10000 respectivamente. Del mismo modo, el símbolo para escribir la unidad fue un símbolo único, y hasta representar 60, ese mismo símbolo se desplaza a la posición inmediata izquierda agregando cero. Cero toma significado de los otros dígitos a la izquierda, aquí cero es un dígito, no es un número. No tiene ningún valor. Quizá importado de la India, donde el cero representa el conjunto vacío.

El valor de un número viene de su lugar en la línea de posición derecha izquierda. Sin embargo, los babilonios consideran al cero el primer número en la recta numérica, solo como un símbolo sin ningún referente a su concepto de número. En resumen, los babilonios crean el dígito cero como marcador del sistema numérico sin lograr conectarlo con alguna noción de número. Esta herencia hasta hoy es clara en el sistema numérico decimal moderno de base 10, es decir, de 10 símbolos: 0,1,2,3,4,5,6,7,8,9. Además, los babilonios emplearon un símbolo para separar los negativos de los positivos, este fue el cero. Desde entonces, hasta hoy, el registro de la cuenta de memoria de las computadoras modernas empieza en el registro del byte 00000000, de allí empieza la cuenta. 

Los Mayas concibieron que la cuenta empieza en cero, a partir de la idea en que el universo se crea de la nada. Los Mayas crearon uno de los mejores calendarios solares y sistemas numéricos gracias a que en su estructura está contenido cero como número.  El propio sistema Maya es posicional, pero además introducen la idea de cifras de base 20, pero con dos tipos de dígitos. El tipo de dígito simple se basa en puntos y líneas, mientras el tipo de cuenta larga emplea un símbolo parecido a un ojo, este cero no es aquí un símbolo, sino un número.

Al cero Maya se llega por divisiones sucesivas 1/1, 1/20, 1/200, 1/200, 1/2000, 1/20000, hasta

Este cero Maya, representa un número que asocia indeterminación de cantidad y es la frontera infinitesimal con la NADA: . A diferencia de otros sistemas como el Egipcio, los mayas hicieron lo obvio, comenzaron a contar desde cero. El calendario Maya se formó de meses de 20 días, numerados de 0 a 20, y no de 1 a 20 como lo hacemos hoy. Combinado con el solar, crearon un calendario con un nombre distinto para cada día, en un ciclo de 52 años.

Los egipcios manejaron las fracciones de manera muy engorrosa, donde cada fracción se puede representar como sumas de 1/n donde n es un número de cuenta. Largas cadenas de fracciones egipcias de la unidad hizo extremadamente difícil codificar la información registrada. El cero Maya hace obsoleto este sistema. Pero los babilonios son los que crean la representación con punto decimal de cifras para fracciones, tal como lo hacemos en el presente en un sistema de base 10. Es claro que el avance tecnológico se hubiera acelerado en Europa, sí los romanos y los griegos no hubieran rechazado a cero. La razón quizá fue que lo consideraran peligroso para los fines religiosos, dado que cero es la ausencia de Dios, del tiempo y del espacio. Es difícil imaginar esto, pero la nada o vacío representó a la muerte. Los griegos creyeron en una frontera hecha por los dioses 1/n, con la idea de átomo, como una forma de asegurar no entrar a la nada, la oscuridad del lenguaje, de la música y de la existencia humana. Los Indios relacionaron al vacío como desorden absoluto, un estado primitivo y natural del cosmos, donde todo empezó. Los Mayas imaginaron esto muy distinto, el cero es una manera de vivir en un plano existencial circular en su historia. La muerte es una forma de saltar a otro círculo existencial. La eternidad del tiempo, el no poder determinar donde termina la existencia y empieza la nada, se le asignó el número cero. Cero representa no el vacío del pensamiento Indio, sino la frontera de indeterminación de lo existente y la nada. Para los Mayas resulta sin ningún temor que el tiempo comenzó en cero, hoy tan importante para la Teoría del Big Bang. 

Además, la problemática de dividir una cuenta entre cero para los babilonios, griegos, romanos resultó algo peligroso. Si bien 1 + 1 no es uno,  cero + cero es cero, este hecho Maya,  violó un principio básico de los números en los axiomas de Arquímedes, que dice que cuando se añade un número a otro número, el segundo cambia su magnitud que representa cantidad. Solo baste con ver 4 + 0 es 4, es un elemento neutro para la suma o la resta, cero no tiene ninguna cantidad asociada, pero

,

amenaza con socavar lo conocido hasta ese momento del conocimiento aritmético. La división y la multiplicación 0/0=0, 0x0=0. Nada a veces cero es cero, el cero Maya irrumpe al advertir que la recta numérica pudiera tener otros infinitos ocultos en la apariencia de continuidad de su numeración, tales puntos serían por ejemplo los irracionales.

No es descabellado pensar que los Mayas llegaran al cálculo infinitesimal antes que Newton y Leibniz, por lo menos no tuvieron temor alguno para explorar el contexto de cero e infinito de la matemática moderna, probablemente allí esté la respuesta de la enorme y asombrosa precisión de sus cálculos. Multiplicar por un número diferente de cero, por cero, destruye al número, reinicia la cuenta, de la misma manera que el reinicio de las computadoras. Solo nos queda especular dado que los españoles destruyeron mucha información, que los Mayas reiniciaron las cuentas al multiplicar por cero; iniciaron la cuenta desde cero, y el propio tiempo y espacio fueron creados desde cero, y la división de un número diferente de cero entre cero no está definida dado que la nada amenaza con destruir los cimientos de la lógica y matemática. Multiplicar por cero solo destruye al número, pero dividir entre cero destruye todo marco de las matemáticas. Cómo tanto poder en un solo número es capaz de impulsar a la ciencia y la ingeniería a límites insospechados de creatividad humana. La entropía o desorden absoluto, o si la prefiere ver como información potencial de un algo es cero orden, es decir, igual a caos absoluto.

Este viaje, es un recordatorio a todos nosotros que el pensamiento matemático es el más grande de los logros de la globalización cultural de la humanidad, y deberá bastar para convencer a los jóvenes, que debieran aprender el pensamiento matemático como un camino acumulativo de conocimiento cultural, en un sentido de menor complejidad a  mayores límites insospechados de matemáticas abstractas. México es heredero de este enorme número cero que creó la revolución de la matemática moderna, honrar con orgullo este hecho debería bastar también, para hacer grandes esfuerzos pedagógicos y que nuestros jóvenes sean mejores que sus profesores, este deseo como el objetivo pedagógico más importante para guiar todo esfuerzo educativo.

Los objetos matemáticos se desarrollan más que se despliegan, y se desarrollan a partir de verdades evidentes (axiomas), para que se conciban nuevos a partir de ese punto, es necesario que el novel los desconstruya hasta sus cimientos (axiomas o teoremas). Al espiarse a sí mismo el novel, puede reconocer su propio camino matemático. Cuanto más explora en lo profundo de los objetos matemáticos, más consciente es el novel, es cuando su actitud para las matemáticas mejora desde un punto en apariencia insoluble, a un estado de nuevos límites interiores dentro del pensamiento matemático. Cada aprendizaje producto no de una habilidad de técnica matemática, sino de un análisis exhaustivo de los principales argumentos que lo definen y resuelven, al agotar los muchos de los aspectos extraños a la curiosidad, además, se gana eficacia en gran parte por precisar el papel de un objeto matemático dentro de otros más complejos.

5.2 Cero

Aunque Occidente temía al vacío, Oriente lo acogió con beneplácito. La India lo considero al cero como el conjunto vacío o la nada. En Arabia cero floreció como un marcador de posición en el sistema numérico. En Egipto floreció como el origen de todo sistema geométrico, es decir, cero dimensiones espaciales. Cero era útil, pero no era realmente un número por sí mismo, no tenía valor. Solo tomó su significado de los dígitos a su izquierda; el símbolo de cero literalmente no significaba nada si no fuera por sí mismo. En la India, todo esto cambió. Fue Alejandro Magno quien lleva el cero babilonio a India. A diferencias de Grecia, la India no tuvo miedo al infinito o al vacío. De hecho los abrazó. 

Al mismo tiempo, sin embargo, para los Indios, el cosmos nunca abandonó realmente su vacío original. Nada era de lo que venía el universo y, lo gran que el concepto nada se convirtió de nuevo en el objeto final de la humanidad. Siendo para los hindúes el cuerpo es la casa del alma, a través de la muerte deja de prestarnos la ilusión de ser reales. Y un hombre es gobernado por un cuerpo y por ello no es libre nunca. Pero una vez que sea capaz de separarse del cuerpo y abrace el silencio y la nada en su alma, será liberado. Atman volará desde la red del deseo humano y se unirá a la conciencia colectiva, el alma infinita que empapa todo el universo, a la vez en todas partes y en ningún lugar y tiempo. Es infinito y no es nada a la vez. Así que la India, como sociedad exploraba activamente el vacío y el infinito, por ello aceptaba cero. Tenga presente que los Mayas, consideraron que nuestro universo no contiene la nada, es decir, en todo lugar siempre hay algo, aunque esto sea el vacío del espacio y el tiempo. 

Los matemáticos Indios hicieron algo más que solo aceptar cero. Lo transformaron, cambiaron su papel de mero marcador babilonio o centro del origen geométrico por la idea de un conjunto vacío. Una vez que los números arrojan su importancia geométrica, los matemáticos ya no tenían que preocuparse por las operaciones matemáticas que tuvieran sentido geométrico. Sin embargo, los Indios, pensaban que cero es un número bastante extraño, por todas las razones que lo implican en la multiplicación y en la división que desata un infierno, al presentarse una no definición de algo entre cero n/0. Para los Indios, 1x0 es infinito. No hay alteración, aunque muchos lo equipararon con Dios infinito e inmutable. Dios fue encontrado en el infinito y en cero.

Sunya, que en India significa vacío, así fue adoptado cero. Cero fue tan importante que  para el nuevo conjunto de números que la gente comenzó a llamar números cifrados o posicionales, los franceses adoptaron el concepto de dígito para cero. Los atomistas siguiendo la idea de Aristóteles, porque este odiaba el vacío, cero era un emblema de la aceptación de dos conceptos: vacío e infinito. Maimónides argumentó que había defectos en la prueba de Aristóteles de que el universo siempre había existido. Después  de todo, entraba en conflicto con las Escrituras Bíblicas. Esto, por supuesto, significaba que Aristóteles termina por irse. Maimónides declaró que el acto de creación del universo vino de la nada, fue creado del vacío, a pesar de la prohibición de Aristóteles. Con ese golpe el vacío pasó del sacrilegio a la santidad^[1].

La iglesia se aferraba a Aristóteles durante siglos, pero con la caída de Aristóteles surgió el vacío y el infinito claramente en la civilización occidental. Fue el momento propicio para que cero llegara del Oeste, a mediados del siglo XII. Cero entró justo cuando Galileo derrumbó con el argumento de Kepler la idea de que nuestro mundo con respecto al universo no está en el centro de todo. 

El hombre que reintroduce cero a Occidente es Leonardo de Pisa, más conocido como Fibonacci, aprendió matemáticas de los musulmanes y pronto se convirtió en un buen matemático por derecho propio. Con sus libros demostró lo útil que eran los números para el comercio y sus cálculos complejos, los banqueros italianos rápidamente se apoderaron del sistema, ocluido el cero. Se crearon tablas de conteo en 1299, Florencia prohibió los números árabes. La razón ostensible era que los números se cambiaban fácilmente y se falsificaban, sin embargo el comercio continuó utilizándolos y es como la palabras para cantidades se llamó cifrado, significó en secreto. 

Al final los gobiernos tuvieron que ceder ante la presión del comercio. La notación árabe se permitió en Italia y pronto se extendió a toda Europa. Cero había llegado, al igual que el vacío. La muralla aristotélica se desmoronó, musulmanes e Indios en 1400 hicieron ver la lógica de Aristóteles como errónea, ya que se basó en sus argumentos en la geometría, cuyas líneas infinitamente divisibles rechazaban automáticamente el atomismo.

Aristóteles creía que el universo existió por siempre. Sugirió un universo eterno sin creación divina. Los que creían en un universo con un comienzo se payaron en un creador llamado Dios. Si existió un comienzo, entonces nos movemos del pasado al futuro y de existir a no existir. Pero Einstein dejó de considerar que la existencias es un fondo que alberga todo lo que está en el tiempo y el espacio, aunque no dijo que es el espacio. La idea fundamental del espacio de la ciencia moderna es la de un tejido uniforme con algunas concentraciones y vacíos locales. El espacio es creado y se extiende en el infinito. Pero el espacio es distorsionado por el tiempo, significa que lo que vemos hoy, no es un estado eterno sino evolución. Las distancias tan grandes en que viaja la luz de galaxias, indicó un comienzo que pudo producirse. Todo se aleja de nosotros, el universo se expande y nada permanece constante en el tiempo más que la energía. En el Bing Bang se originó el universo, al teoría M nos dice que tenemos tres  dimensiones grandes casi planas y sobre ellas otras siete dimensiones cortas dobladas sobre estas primeras. La suma total de la energía del universo es cero, la energía oscura y la energía materia, son simétricas a la energía que representa el espacio. 

Sucede que cero en algún momento, pero no es fácil de ver cómo puede llevarnos a la idea que en un sentido es algo. 

5.3 Definición de diferenciabilidad 

El cero Maya, es una idea de que la unidad entre infinito es una , un infinitesimal , algo con infinitos ceros después del punto decimal y justo al final un uno. Esta diferencia , es un viaje de descenso infinito en la división.

Formalmente, agregamos etiquetas que nos ayudará cuando lleguemos a generalizar, y hay dos notaciones comunes en uso. La primera implica un punto principal a y un punto vecino x, 

Formalmente, agregamos etiquetas que nos ayudará cuando lleguemos a generalizar, y hay dos notaciones comunes en uso. La primera implica un punto principal a y un punto vecino x; la segunda, se refiere a un punto principal x y un a vecino. 

Ahora lo generalizamos para una curva:

La línea que une los puntos (a,f(a)) y (x,f(x)) ya no es una tangente en el gráfico, por lo que le damos el nombre de recta secante. Pero la línea secante se acerca a ser una línea tangente si nos acercamos de x a a. 

Esta es la idea utilizada por los matemáticos. Imaginamos que el punto de movimiento se acerca cada vez al punto principal, arrastrando consigo la recta secante, hasta que, en el límite, la línea secante se convierte en la línea tangente. para capturar este proceso lo escribimos así

o

En la primera expresión, se lee como f prima de a; en el la segunda, evaluando en a. Para ambas se lee 

El límite cuando x tiende a de f de x menos de de a entre x menos a. 

Es posible que desee comprobar que podría escribir la misma información utilizando el otro sistema de etiquetado. Estas fórmulas nos dan la derivada como resultado, en realidad vemos una definición de la derivada como una generadora de funciones que nos dan todos los ángulos de las rectas tangentes a la curva que derivamos. En una nomenclatura de Newton:

Observe que no se trata del valor del límite, se trata de la existencia del límite en todo lo infinito del dominio de una función. La frase siempre existe un límite es la clave, se dice que una función es diferenciable si existe este límite.

5.4 Evaluación de la derivada 

La diferenciación, entonces, se trata de la existencia o no de un límite. Así que podemos aprender mucho mirando cómo tal límite podría no existir, lo que significa que una función no es diferenciable en un punto dado. En primer lugar, aplicaremos la defección de la derivada para confirmar que los gradientes salen como esperamos para cada punto de una curva.

Considere dada por . Usando la formulación que implica , aquí demostraremos que existe la derivada y encontremos la recta tangente en x=3

Demostración

nosotros aplicamos la definición de la derivada

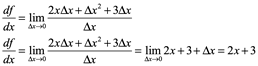
Así que tenemos 

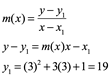
Si es 3 

es ?

La recta tangente está en el punto P(3,19)

Aplicando la ecuación de la recta:

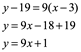
Hay varias cosas a tener en cuenta acerca de la forma en que está escrito esto. En primer lugar, hay dos declaraciones explícitas que las ecuaciones contienen para todos . Esto es una buena práctica porque en algunos casos diferentes valores de x dan resultados diferentes y, porque es educado para un lector, mejor tener demasiados lugares donde especificamos lo que estamos hablando que muy pocos. En segundo lugar, la demostración presenta todo el álgebra para el cociente diferencial antes de discutir su límite. Siempre aconsejamos a los estudiantes que trabajen de esta manera porque la gente a menudo comete errores cuando no lo hacen. En particular, tienden a poner límite delante de la primera expresión, luego se le olvida, por lo que escriben solo el cociente.

5.5 Tablas de teoremas de derivación 

En el análisis diferencial se encontrará con muchos teoremas (demostraciones de casos) que le permitirán la diferenciabilidad. 

1) Teorema álgebra de derivadas:

Supongamos que y que y son diferenciables

Entonces

1. f + g es diferenciable en a con 

el papel de suma de funciones 

2. cf es diferenciable en a con el papel de un constante por una función.

Algunos estudiantes les parece rara que escribamos esto así, porque parece obvio eso y son lo mismo. Pero esto es realmente un teorema sobre el orden de las operaciones. En , se agrega las funciones y a continuación, se diferencia el resultado. En , las funciones se diferencian y a continuación se agregan los resultados. En matemáticas más ampliamente, no es obvio que las órdenes de operación se puedan cambiar sin cambiar el resultado. Este teorema dice que siempre todas las derivadas están sensiblemente definidas en el cambio de tarea para derivarlas. 

Nos gusta usar este teorema para sacar a los estudiantes de cualquier complacencia. 

3. fg es diferenciable en a con

Demostrar la regla del producto implica un buen truco, pero las pruebas de todos estos resultados implican trabajar directamente con la definición de Newton y dedicar a trabajar la simplificación directamente hasta llegar a la fórmula de derivación. 

Un teorema que produce grandes resultados en el análisis diferencial es el teorema de Rolle y el teorema del valor medio.

2) Teorema de Rolle 

Supongamos que es continuo en y diferenciable en (a,b) y f(a)=f(b) . Entonces de tal manera que

Un teorema es una declaración sobre una relación entre conceptos. Por lo general, se trata de una relación que se mantiene en general, donde utiliza esta frase en el sentido matemático; cuando los matemáticos dicen en general, menudo significa para todos los casos, no solo en la mayoría de los casos. Un teorema posea premisas y conclusiones.

Todos los teoremas tienen una o más premisas -cosas que sumimos verdaderas- y una conclusión, algo que definitivamente es cierto si las premisas son verdaderas. En este caso para Teorema de Rolle, las premisas están marcadas con la palabra “supongamos”.  Para este teorema son

Que f es una función definida en un intervalo .

Que f es continua en el intervalo .

Que f es diferenciable sobre el intervalo .

Que f(a)=f(b)

La conclusión está marcada por la palabra “entonces”, en este caso es que existe tal que . La notación significa que la derivada de f en c es cero, y el teorema nos dice que existe un punto c en con esta propiedad (el intervalo abierto es el conjunto que contiene todos los valores entre a y b pero son incluir a a o  b).

El teorema de Rolle nos dice que exactamente dónde está c, los teoremas de existencia como este son bastantes comunes en las matemáticas avanzadas.

Al igual que con las definiciones, podemos pensar en cómo los teoremas se relacionan con los ejemplos. En este caso, podemos preguntar cómo el teorema se aplica a funciones específicas. Para satisfacer las premisas, es necesario definir una función  en un intervalo cerrado [a,b]. Así que tenemos que decidir sobre una función y sobre valores para a y b. Por ejemplo con a=-3 y b=3, entonces f(a)=f(b). f es continua y diferenciable en todas partes, por lo que todas las premisas están satisfechas. Por lo tanto, la conclusión sostiene: existe c en tal que en (a,b) en este caso la derivada que sin duda en este caso la derivada pasa a ser cero en c=0, que es sin duda entre -3 y 3. 

El siguiente diagrama nos convence de la generalidad del teorema de Rolle:

3) Teorema del valor medio

Supongamos que es continuo en y diferenciable en (a,b). Entonces de tal manera que 

Demostración

Supongamos que f es continua en [a,b] y diferenciable sobre (a,b)

Definimos por

Ahora 

es un polinomio en x

Así d es continua y diferenciable por la suma y las reglas de multiplicación de contante por función.

Tenga en cuenta que 

Además 

y

Así que el Teorema de Rolle se aplica a d en [a,b]

Así que entonces d’(c)=0 que es entonces

Así entonces 

según sea necesario.

Recuerde que las características más destacadas de una función f son:

(a) El conjunto en el que se define f, llamado dominio de f y escrito dom(f);

(b) La asignación, regla o fórmula que especifica el valor f(x) de f en cada x en dom f).

Nos ocuparemos de las funciones f de forma tal que dom (f) ⊆ R y tal que f sea una función de valor real, es decir, f(x)∈R para todo x ∈ dom (f). Hablando correctamente, el símbolo f representa la función, mientras que f(x) representa el valor de la función en x. Sin embargo, a menudo se proporciona una función especificando sus valores y sin mencionar su dominio. En este caso, se entiende que el dominio es el dominio natural: el subconjunto más grande de R en el que la función está bien definida con valor real. Entonces "la función f(x) = 1/x " es la abreviatura de "la función f dada por f(x) = 1/x con dominio natural {x ∈ R: x 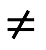0}". Del mismo modo, el dominio natural de g (x) = √(4 - x²) es [−2, 2] y el dominio natural de csc x = 1/sen x es el conjunto de números reales x no de la forma nπ, n ∈ Z.

Sea f una función de valor real cuyo dominio es un subconjunto de R. La función f es continua en x₀ en dom(f) si, para cada secuencia (x_n) en dom(f)  converge en x₀, tenemos lim_n f(x_n) = f(x₀). Si f es continua en cada punto de un conjunto S ⊆ dom (f), entonces se dice que es continua en S. La función f se dice que es continua si es continua en dom(f).

Nuestra definición implica que los valores f(x) está cerca de f(x₀) cuando los valores x están cerca de x₀. El siguiente teorema dice esto de otra manera. De hecho, la condición (1) del siguiente teorema es la definición de continuidad 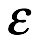, δ dada en muchos libros de cálculo.

[1] Klein-Braslavy, Sara. (2019). Maimonides as Biblical Interpreter. 10.1515/9781618110435.

______________________________________

Autores:

Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Lizbeth Guadalupe Villalon Magallan
Mónica Rico Reyes
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán