Pensamiento Matemático
proceptual-simbólico
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Filo Enrique Borjas García
Rogelio Ochoa Barragán

Lección 8: Conceptos precursores a la derivada
Isaac Newton escribió a Robert Hooke, por cierto alguien a quién no estimaba mucho, el 5 de febrero de 1676, la frase: “Si he logrado ver más lejos, ha sido porque he subido a hombros de gigantes”. Es en esta frase que nos inspiramos para abrir nuestra ignorancia a la luz en el ámbito de las matemáticas, hay una gran verdad, la verdad se construye entre todos los que la buscan como fundamento de la visión científica moderna. Newton deja ver que todo conocimiento nuevo es herencia del esfuerzo de predecesores, en su caso Copérnico, Galileo y Kepler. Un hito de las matemáticas es el cálculo infinitesimal, intentaremos hacer de la misma manera una construcción histórica, lingüística y conceptual de la derivada, con el fin de reconocer en ella el primer gran esfuerzo global de la humanidad, aunque para algunos esté claro que Newton y Leibniz son los creadores de este cálculo de infinitesimales, es decir, de tasas de cambio instantáneas. La necesidad obedecía a las fallas de las herramientas matemáticas de cálculo de la época, en su sentido de precisión y exactitud.
El primer hito de la historia lo situamos en el libro de Euclides “Elementos”, la interpretación de la derivada tiene como predecesores los conceptos de punto, línea, círculo, curva, función, punto tangente, polígono regular, hipotenusa, plano cartesiano, entre otros.
Un punto es lo que no tiene partes.
Una línea es una longitud sin anchura.
Los extremos de una línea son puntos.
¿El cálculo infinitesimal es exacto o de aproximación?
¿Qué clases de infinitesimales?
De rango, de superficie, de volumen, vectoriales, de arco, …
Línea recta
Una línea recta es una figura unidimensional que no tiene espesor y se extiende infinitamente en ambas direcciones. Una línea a veces se llama línea recta o, más arcaica, una línea a la derecha, para subrayar que no tiene "distancias negativas" en cualquier lugar a lo largo de su longitud. Mientras que las líneas son intrínsecamente objetos unidimensionales, que pueden estar incrustados en espacios dimensionales más altos, es un borde de un gráfico una "línea". Una línea está unívocamente determinada por dos puntos, y la línea que pasa por los puntos, de manera similar, la longitud del segmento de línea finita que termina en estos puntos pueden estar indicados. Una línea también puede estar indicada con una sola letra minúscula, Euclides definió una línea como una "longitud sin anchura", y una línea recta como una línea que "yace por igual respecto de los puntos en sí mismos". Consideremos primero las líneas en un plano bidimensional. Dos rectas en el mismo plano que no se cruzan entre sí se dice que son líneas paralelas. Dos líneas situadas en planos diferentes que no hay intersección entre sí, se dice que son líneas oblicuas.
La línea con intersección x=a y la línea con intersección y=b vienen dadas por la forma de intersección:
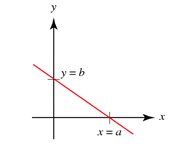
![]()
La línea a través, ![]() la pendiente está dada por la forma punto-pendiente
la pendiente está dada por la forma punto-pendiente
![]()
Determinan una ecuación de la recta:
![]()
En forma de un sistema lineal:
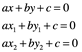
Este sistema es homogéneo, tiene una solución no trivial sí y solo si el determinante de la matriz de coeficientes es cero, esto es:
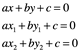
De esta manera, todo punto de la recta satisface al determinante, es decir, pertenece a la recta.
Por ejemplo, hallar la ecuación de la recta en los P(-1,-3) y Q(4,6), al sustituir:
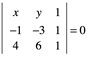
Al desarrollar el determinante:
-3x+5y-18=0
Ecuación vectorial de la recta:
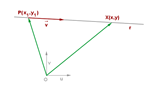
P es un punto de la recta r, el vector ![]() tiene igual dirección de
tiene igual dirección de ![]() , que es un vector dirección sobre r, el vector
, que es un vector dirección sobre r, el vector ![]() es igual al vector
es igual al vector ![]() multiplicado por un escalar k, es decir, el producto interno
multiplicado por un escalar k, es decir, el producto interno ![]()
![]()
![]()
Por ejemplo, una recta pasa por el punto X(-1,3) y tiene como vector dirección ![]() =[2,5]
=[2,5]
Su ecuación vectorial de la recta estaría dada por
![]()
Para aproximarnos a la ecuación paramétrica de la recta
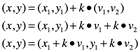
La igualdad de vectores es desdoblada en dos igualdades escalares, a esto se le llama ecuación paramétrica de la recta.
![]()
despejando k
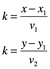
![]()
![]()
Por ejemplo, una recta pasa por el punto X(-1,3) y tiene como vector dirección ![]() =[2,5] encuentre su ecuación paramétrica en función de t:
=[2,5] encuentre su ecuación paramétrica en función de t:
![]()
Dados los puntos X(-1,3) y P(1,8) encuentre la ecuación de la recta en su forma y=mx+b sí =[2,5] aplicando
![]()
![]()
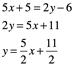
Una forma vectorial alternativa de la recta es ![]() , donde n es un vector normal a la recta, P es un punto de la recta. El vector n se obtiene de los coeficientes de la ecuación de la recta en su forma x+y=p
, donde n es un vector normal a la recta, P es un punto de la recta. El vector n se obtiene de los coeficientes de la ecuación de la recta en su forma x+y=p
![]()
Por lo tanto, n es
![]()
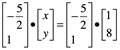
Forma vectorial de la recta.
Otras expresiones útiles son:
Para hallar la distancia al origen de una recta r, ax+by+c=0
![]()
La ecuación paramétrica en R3,
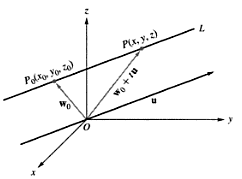
Donde ![]() es el vector asociado con
es el vector asociado con![]() , x el vector asociado al punto P(x,y,z). La recta L, que pasa por
, x el vector asociado al punto P(x,y,z). La recta L, que pasa por ![]() , y es paralela a u, donde u es un vector dirección sobre L.
, y es paralela a u, donde u es un vector dirección sobre L.
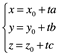
donde u=[a,b,c]
![]()
![]()
Por ejemplo, encuentre las ecuaciones paramétricas para L que pasan por el punto ![]() y vector dirección u=[2,-3,4]
y vector dirección u=[2,-3,4]
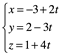
en su forma L en![]() es un plano, por lo tanto
es un plano, por lo tanto![]() , donde n es un vector normal al plano L.
, donde n es un vector normal al plano L.
n=[a,b,c]
![]()
donde la ecuación del plano es
ax + by + cz + d=0
Como ejemplo determine una ecuación del plano que pasa por los puntos P(2,-2,1), Q(-1,0,3) y R(5,-3,4) (método uno). Elaboramos el sistema de ecuaciones para un plano determinado por tres puntos.
![]()
Al resolver el sistema
![]()
r es cualquier número real, nos conviene r=17.
![]()
Por un método dos, como lo efectuamos para el caso en ![]() ,
,
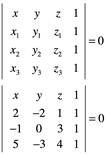
Al operar este determinante nos da:
![]()
Por un método tres, a través del producto cruz, y la ecuación plano ![]() .
.
Los vectores ![]() y
y ![]() están en el plano, ya que los tres puntos están en el plano, entonces el vector n normal al plano,
están en el plano, ya que los tres puntos están en el plano, entonces el vector n normal al plano, ![]() x
x ![]() :
:
![]()
![]()
n=![]()
Si utilizamos n y el punto ![]() , obtenemos la ecuación del plano:
, obtenemos la ecuación del plano:
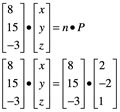
![]()
![]()
Ejemplo para determinar dos planos cuya intersección es la recta paramétrica:
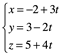
Determinamos la ecuación de la recta en forma simétrica,
![]()
![]()
Entonces la recta dada es la intersección de los planos,
![]()
y
![]() entonces los planos son,
entonces los planos son,
2x+3y-5=0
y
4x-3z+23=0