Pensamiento Matemático
proceptual-simbólico
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Filo Enrique Borjas García
Rogelio Ochoa Barragán
Lección 7: Nuestra herencia en el sol
La matemática por su precisión e inequívoca dinámica puede satisfacer criterios de refutación, de creación de nuevos objetos matemáticos con autonomía y en apariencia sin límites. Sin embargo, en el discurso de la enseñanza, el lenguaje natural agrega su naturaleza imprecisa con el fin de formar una narrativa que construya una experiencia de conocimiento y articule el tiempo en forma de vivir un aprendizaje. El aturdidor silencio de la matemática, ocasiona en muchos noveles una muerte de la vía semántica, es decir, una frustración en la interpretación de proposiciones matemáticas, en consecuencia, se nos niega el acceso al propio mundo platónico. El lenguaje natural dota de la sensibilidad necesaria para la memoria de largo plazo, incluyendo la simbología de la notación matemática, tal como lo hace, para la razón dentro de un poema el propio ritmo, como un factor de relación en nuestra memoria.
La cuenta de los soles llevó a los Mayas a la construcción del cero moderno, de cálculos asombrosos y fuertemente documentados en las esferas de la comunidad astronómica internacional, historia única que nos hace reflexionar sobre los hechos arquitectónicos emparejados con la cúpula celeste; debió haber factores culturales que motivaron a esta civilización a calcular con ayuda de las matemáticas el tiempo, el espacio y la información. Sin embargo, parece que fue también un asunto de elites, privilegiados que en la vida intelectual de sus comunidades plantearon una cosmovisión orientada al saber vivir, en función de conceptualizar la muerte. Siendo la realidad algo extraño, que nos sorprende en el viaje a su interior, la única navegación segura o más segura que hemos encontrado en el ámbito del conocimiento objetivo, es la matemática. El camino de la matemática es la búsqueda de la verdad que superpone la supervivencia individual y colectiva de una civilización. Su ausencia en una sociedad, es un factor de decadencia de permeable corrupción al desdeñar en la educación de sus ciudadanos, los valores del desafío intelectual inherente al lenguaje matemático, es decir, la indagación intelectual encaminada al discernimiento responsable de la realidad por la vía matemática, es un factor de tolerancia democrático necesario para construir acuerdos en comunidad.
Un ciudadano con más recursos para argumentar, es un ciudadano que más se aleja de la violencia y más se aproxima a su libertad creativa. Una ruta de aprendizaje de las matemáticas, es como un poema que abre un nuevo comienzo, que sus enunciados habitan en el mundo platónico; demarcación que identifica la cultura occidental. Nuestra propuesta es aspirar a renovar el encanto e iluminar el camino sistémico, simbólico y de aplicación tecnológica para nuevos ciudadanos que en la matemática puedan encontrar el nuevo diálogo para su propio progreso.
La herencia matemática
Las matemáticas nacieron con la razón, el habla y la consciencia, hace unos 10,000 años, quedaron impresas sus marcas en tablas de arcillas[1] en el Oriente Próximo. De la acción de marcar se pasó a símbolos sistematizados por los antiguos babilonios[2], movimientos de sucesos celestes periódicos fueron registrados y calculados; la agricultura avanzó con los calendarios; las matemáticas se convirtieron el ritmo cultural de una época, son la antesala de nuevas tecnologías; de la astronomía a la agricultura, del comercio con aritmética, en el comercio con Internet: teoría de la información, proceso de señales electromagnéticas, topología de redes,…, esta historia de un universo numérico se está volviendo más abstracta, ahora explorando los espacios multi - dimensionales y la dinámica del caos.
Un texto clave de la historia de las matemáticas son los 5 libros que sobreviven de Euclides los Elementos, la división de figuras, los datos, los fenómenos y la óptica[3]. El libro quinto, los elementos, nos introduce a conceptos geométricos básicos, compuestos por 465 proposiciones divididas en 13 capítulos:
1) triángulos
2) rectángulos
3) círculos
4) polígonos
5) proporción
6) similitud
7-10) Teoría de los números
11) geometría sólida
12) pirámides
13) sólidos platónicos
Elementos se compone de 23 definiciones, cinco postulados y cinco "nociones comunes", y sistemáticamente la geometría plana y sólida. Los cinco postulados de Euclides son:
1. Es posible trazar una línea recta desde un punto a otro punto.
2. Es posible producir una línea recta finita continuamente en una línea recta.
3. Es posible describir un círculo con cualquier centro y radio.
4. Todos los ángulos rectos son iguales entre sí.
5. Si una recta que corta a dos rectas hace los ángulos interiores del mismo lado menores que dos rectos, las líneas rectas (si se extiende indefinidamente) se reúnen en el lado que están los (ángulos) menores que dos rectos.
El quinto postulado es conocido ahora como el de paralelas, destacamos que Euclides dejó inconcluso su trabajo, por ejemplo Hilbert necesitó de 20 postulados para completar la lógica de la geometría. Las geometrías no euclidianas: hiperbólicas, elípticas, esféricas son coherentes para los primeros cuatro postulados, en 1868 Beltrami lo demostró[4]. Los pitagóricos practicaron una filosofía de un universo basada en los números, se pasó de los números naturales (1,2,3,4…) a un segundo tipo llamado fracciones o números racionales (un número racional es una fracción a/b donde a y b son números naturales donde b es diferente de cero), cuando las fracciones no son exactas, es decir, es un número que no puede ser expresado como una fracción de enteros, son decimales en expansión infinita. El más famoso es llamado constante de Pitágoras (
), que según una leyenda le costó la vida a Hiparco al expresar su descubrimiento[5]. A los números enteros y racionales se les llama también números elementales y se aplican en métodos aritméticos, geométricos y en el álgebra arábiga. La teoría de números es un campo vasto y fascinante de las matemáticas, a veces llamada "aritmética superior", que consiste en el estudio de las propiedades de los números enteros. Primos y descomposición en factores primos son especialmente importantes en la teoría de números, al igual que una serie de funciones, como la función divisor, la función zeta de Riemann, y la función totient[6]. Un número llamado a la historia sin duda fue pi (
), que al principio fue observado como la razón entre la circunferencia de un círculo y su diámetro, llamado constante de Ludolfo, Legendre demostró que pi es un número irracional y en 1963 mediante una construcción geométrica se da una fracción de aproximación muy aceptable 355/113[7] o 
. Esto aproximó la idea de un círculo como un polígono regular de 
número de lados, tan necesaria para el cálculo infinitesimal de Newton. Un problema que también fue famoso es la cuadratura de un círculo, es construir un cuadrado con la misma área de un círculo dado. El sistema occidental de símbolos numerales 0,1,2,3,4,5,6,7,8,9 evoluciona del Hindú (800 a.C.), Arábigo (900 a.C.), español (1000 a.C.), Italiano (1400 a.C.), las piezas estarían completas cuando se evoluciona del cero Hindú (conjunto vacío[8]) al cero Maya que representa indeterminación de cantidad[9] (40 a.C.)
Tabla de Cálculo de los eclipses del códice Dresde, en el cual se puede ver la aplicación del Cero Maya
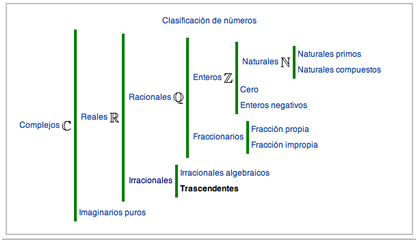
Los números naturales, N (enteros positivos) se cree que están de manera innata presentes en los humanos[10], origen genético que da origen a la construcción de las matemáticas, esta capacidad está presente de manera primitiva también en chimpancés y aves[11], se incluye al cero o se excluye al definirlos por algunos matemáticos N={0,1,2,3,4,5,6,7,8,9}. Cuando agregamos a este conjunto los negativos tenemos a los enteros, Z (por la palabra alemana Zahlen, números). Los números racionales (Q, por la palabra alemana Quotient traducida como cociente) son los que se expresan como una fracción a/b donde a y b son enteros y b es diferente de cero, los números enteros también son racionales porque pueden ser expresados con denominador 1, la recta numérica real se forma de la unión de números racionales e irracionales, constituyen los números reales R. Los números que son algebraicos son los reales o complejos que satisfacen una ecuación polinómica, son las raíces no cero que satisfacen: 
, de lo contrario, se llaman trascendentales a aquellos como pi, e, ln 2, sen (1). Los números complejos C, contienen a los R, además, a diferencia de los reales incluyen todas las raíces de los polinomios, están formados por una parte real y una imaginaria. Los números C, son un cuerpo o campo, en otras palabras son una estructura algebraica cerrada bajo las operaciones de suma y multiplicación, un complejo que denota z= Re(z) + Im(z) o z=a +bi, se le llama puro si solo está formado por la parte imaginaria Im(z),
.
Las matemáticas avanzan más allá de la idea de número, dan lugar a una generalización del mismo en forma de variable algebraica, dando origen a lo que llamamos álgebra, un siguiente nivel de abstracción en la historia de las ficciones platónicas. Aunque la aritmética ya existía, este gran paso supuso el nacimiento del cálculo moderno. Los símbolos representan números, como parte de soluciones de ecuaciones. Las ecuaciones eran recetas babilónicas sobre tablillas de arcilla expresadas en forma geométrica, la palabra viene del árabe al-jabr. Es por ello, que el álgebra de polinomios se le llama álgebra arábiga. El álgebra evoluciona a su siguiente generación llamada abstracta, aparecen nuevas álgebras tales como Banach, Booleana, Borel, Clifford, Cayley, Sigma, Steenrod, Neuman, Umbral, Hecke entre muchas otras. Aunque en la escuela se nos separa a la matemática por conveniencia en: aritmética, álgebra, geometría, teoría de números, …, en realidad la disciplina de ficciones está muy fuertemente unida, muchos avances tecnológicos de hoy se deben a fusiones como la teoría de la información y los campos de los sistemas dinámicos.
En el campo de la geometría los avances son notables, la geometría euclidiana, los sistemas de coordenadas (polares, rectangulares, esféricos, cilíndricos), la geometría estudia las figuras, los objetos y sus relaciones en el espacio geométrico. Contrasta con el álgebra que estudia cantidades numéricas y soluciones de ecuaciones. En geometría conceptos comunes son: área, ángulo, perímetro, paralelas, perpendicular, esfera, polígono, cilindro, cubo, radio, hipotenusa, triángulo, volumen, dimensiones, circunferencia, curva, punto, recta, parábola, latitud, longitud, trapecio, rectángulo,…, Además, en las geometrías no euclidianas, los ejes de referencia son curvas, como la hipergeometría, elíptica y esférica.
Una geometría no euclidiana, también llamada Lobachevsky-Bolyai-Gauss (geometría hiperbólica), con curvatura seccional constante. Esta geometría satisface todos los postulados de Euclides excepto el postulado de las paralelas, que se modifica como sigue: “Para cualquier línea recta infinita y cualquier punto no sobre ella, hay muchas otras que se extienden infinitamente, líneas rectas que atraviesan y que no se cruzan”. En esta la suma de los ángulos de un triángulo no es 180º y no hay triángulos semejantes. El espacio hiperbólico más conocido son las esferas de Lorentz de cuatro dimensiones[12], en física son llamados agujeros de gusano de Lorentz[13],.
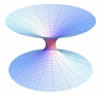
La geometría elíptica o llamada Riemann se puede visualizar como la superficie de una esfera en la que las líneas se toman como círculos grandes, en esta la suma de los ángulos de un triángulo es >180º. En cuanto al postulado de las paralelas dice: a través de cualquier punto en el plano, no existen líneas paralelas a una recta dada[14].
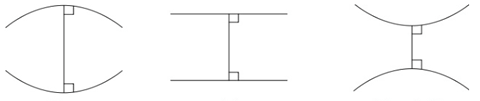
Elíptica Euclidiana Hiperbólica
La geometría esférica es el modelo en el cual una línea no tiene ninguna línea paralela a través de un punto dado[15]. El ángulo entre dos líneas en la geometría esférica es el ángulo entre los planos de los grandes círculos correspondientes, y un triángulo esférico se define por sus tres ángulos. No existe el concepto de semejanza de triángulos en la geometría esférica[16].
Por otro lado, el álgebra abstracta es el conjunto de temas avanzados del álgebra que tienen que ver con las estructuras algebraicas abstractas, en lugar de los sistemas de números habituales. La más importante de estas estructuras son grupos, anillos y campos. Ramas importantes del álgebra abstracta son el álgebra conmutativa, teoría de la representación y álgebra homológica. Álgebra lineal, la teoría elemental de números y matemáticas discretas a veces se consideran ramas del álgebra abstracta.
[1] Schmandt-Besserat, Denise (1998) Animal Symbols at “Ain Ghazal. Expedition 39(1):48-58
[2] Martos, Quesada, J. (2001) Los estudios sobre el desarrollo de las matemáticas en al-Andalus: estado actual de la cuestión. DYNAMIS 21:269-293. Consultado: 23 de Febrero de 2013, de www.raco.cat/index.php/Dynamis/article/download/92578/117793
[3] Wussing H. (1998) Lecciones de historia de las matemáticas. Madrid: Siglo XXI
[4] Greenberg, M. J. (1994) Euclidean and Non-Euclidean Geometries: Development and History, San Francisco, CA: W. H. Freeman.
[5] Gourdon, X. and Sebah, P. "Pythagore's Constant: ." Consultado: 23 de Febrero de 2013. http://numbers.computation.free.fr/Constants/Sqrt2/sqrt2.html
[6] MathPages. "Number Theory." Consultado: 23 de Febrero de 2013. http://www.mathpages.com/home/inumber.htm
[7] Ramanujan, S. (1963) "Modular Equations and Approximations to pi." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
[8] A-BAK’2013 el sol del nuevo B’aktun. Consultado: 23 de Febrero de 2013, de http://abakmatematicamaya.blogspot.mx/2010/04/bak-matematica-maya-el-cero-maya.html
[9] Estévez Delgado, G. & Ochoa H., E. (2001) El origen del cero. Morelia: UMSNH. Consultado: 23 de Febrero de 2013, de http://dieumsnh.qfb.umich.mx/matematicas/cero.htm
[10] Díaz, D., Ruy (2001) Adquisición de la noción de número natural. Rev. Iberoamericana de la educación 49:5-25. Consultado: 23 de Febrero de 2013, de http://www.rieoei.org/deloslectores/2618Diaz.pdf
[11] Gelmam, Rochel (2004) Languaje and the origien of numerical concepts. Science 306(5695):441-443. Consultado: 23 de Febrero de 2013, de http://ruccs.rutgers.edu/~rgelman/index.html
[12] Albujer Brotons, Alma Luisa (2009) Geometría global de superficies espaciales en espacios producto lorentzianos. Murcia: Universidad de Murcia. Consultado: 24 de Febrero de 2013, de http://digitum.um.es/xmlui/bitstream/10201/3263/1/AlbujerBrotons.pdf
[13] Méndez, R., Juan (2008) Agujeros de gusano rotante con materia escalr tipo phantom. CINVESTAV. Consultado: 24 de Febrero de 2013, de http://pelusa.fis.cinvestav.mx/tmatos/LaSumA/3_RecursosH/MenC/Juan_Mendez.pdf
[14] Martin E., George (1991) The Foundations of geometry and the non-euclidean plane. Springer. Consultado: 24 de Febrero de 2013, de E-Book
[15] Polking C., John (1996)The Geometry of the sphere. Rice University Consultado: 24 de Febrero de 2013, de http://math.rice.edu/~pcmi/sphere/#intro
[16] Hopf, H. "Selected Chapters of Geometry (1940) ETH Zürich lecture, pp. 1-2. Consultado: 24 de Febrero de 2013, de http://www.math.cornell.edu/~hatcher/Other/hopf-samelson.pdf