Texto académico
Autores
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Gladys Juárez Cisneros
Lizbeth Guadalupe Villalon Magallan
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán

_____________________________
5. Ecuación de onda cuántica
5.1 Fasor
Al reunir los conceptos del plano complejo, las relaciones de Euler nos llevan a los fasores. El fasor es una poderosa herramienta para el análisis de la función de onda,![]() . Para comprender esto, consideremos dos ondas:
. Para comprender esto, consideremos dos ondas:
![]()
Si las amplitudes están dadas por ![]() , la longitud de las ondas por
, la longitud de las ondas por ![]() y la frecuencia angular
y la frecuencia angular ![]() , entonces, la única diferencia son las constantes
, entonces, la única diferencia son las constantes ![]() , si
, si
![]()
Entonces:
![]()
Para trazar estas funciones de onda en un gráfico bidimensional, debemos decidir si verla como una función de onda en espacio x o en función de tiempo t. Si decide en el espacio ver la onda, considere t=0:
![]()
Sería algo así:
 14.48.46.png)
Tenga en cuenta que la constante de fase ![]() , tiene el efecto de desplazar la segunda función de onda a la izquierda, ya que la constante de fase y el término x tienen el mismo signo (es decir, ambas son positivas). Además, el desplazamiento de fase positivo en radianes (90º), con el efecto de convertir una función senoidal en una función coseno, ya que
, tiene el efecto de desplazar la segunda función de onda a la izquierda, ya que la constante de fase y el término x tienen el mismo signo (es decir, ambas son positivas). Además, el desplazamiento de fase positivo en radianes (90º), con el efecto de convertir una función senoidal en una función coseno, ya que
![]()
Ahora, considere lo que sucede cuando elige trazar estas ondas como una función del tiempo t en lugar de la distancia x. Así como tenía que elegir un momento específico al trazar frente al espacio, ahora debe seleccionar un valor específico de x en el que su tiempo se aplica. Seleccionaremos x=0, las funciones son:
![]()
En estas figuras al trazarlas juntas:
 14.51.35.png)
Se observa que esta segunda onda aparece retrasada, algunos consideran esto confuso porque parece que es la onda uno la que inició tarde, pero recuerde que el tiempo está aumentando a la derecha en esta trama, por lo que los picos de la onda dos ocurren antes, es decir, a la izquierda. Por lo tanto, en una trama en el tiempo que aumenta a la derecha, las ondas líderes aparecen a la izquierda de las ondas restantes, posicionadas a la derecha.
Los diagramas de Fasor pueden ser extremadamente útiles al analizar la onda como y1 y y2. Pero, dado que estas ondas están descritas como ondas senos y cosenos, podemos representarlas como:
![]()
Euler relaciona:
![]()
Observe lo que sucede con:
![]()
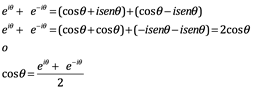
Esto es útil. Muestra que la función del coseno puede ser representada por dos fasores contrarrotantes, ya que ![]() aumenta rotando
aumenta rotando ![]() y antirrotando
y antirrotando ![]() en el sentido de las manecillas del reloj, como se muestra:
en el sentido de las manecillas del reloj, como se muestra:
 15.06.02.png)
Para comprender cómo los fasores contrarrotantes ![]() se suman para varios valores de
se suman para varios valores de ![]() ,
,
 15.07.59.png)
Por lo tanto, la función del coseno puede ser representada por dos fasores contrarrotantes
![]()
Y en cualquier ángulo la suma de esos fasores y divididos por 2, produce el valor del coseno de ese ángulo. ¿Puede la función seno ser representada de esta manera?
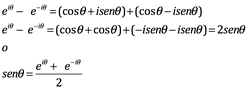
Este resultado también demuestra que la función senoidal puede ser representada por dos fasores contrarrotatorios.
 15.13.20.png)
Y
 15.14.19.png)
En algunos libros, se utiliza la versión simplificada de la representación de los fasores sinuosoidales. En esa versión, el plano complejo se presenta como un par de ejes perpendiculares, y el valor de la función se toma como la proyección de un fasor de longitud A en el eje vertical. El ángulo de fasor con respecto al eje horizontal positivo (hacia la derecha), a menudo se etiqueta ![]() y se da por el
y se da por el
 15.19.18.png)
Otro concepto importante, es que a veces se hace confuso el significado de frecuencia negativa. La confusión surge de que la frecuencia es el inverso del periodo y el periodo es simplemente un número positivo. Entonces, ¿cómo puede ser negativa la frecuencia? La respuesta es que es un valor negativo para el significado de haber tomado la convención de la dirección para las velocidades, en sentido anti horario negativo y caso contrario positiva. Por lo tanto, los fasores de contrarrotación componen funciones senos y cosenos, podemos considerar como fasor con frecuencia positiva (rotación en sentido anti horario), y otro fasor con frecuencia negativa (en el sentido de las agujas del reloj). Esto resultará particularmente útil en el análisis de Fourier.
Ya en este punto, hemos estudiado la ecuación de onda para su propagación electromagnética, y ahora es el turno de su versión cuántica. Aunque las ondas mecánicas son las más obvias para nuestra vida cotidiana en forma de sonido musical, en estanques de agua o cuerdas de guitarra; las ondas electromagnéticas sin duda son las más útiles para nuestra sociedad electrónica informática, y se puede argumentar que las ondas cuánticas son aún más fundamentales para la vida moderna. Cada pedazo de materia de este universo bajo ciertas circunstancias se comporta de manera cuántica, por lo que es difícil imaginar algo más fundamental para la formación de una mente de un joven estudiante moderno. Gran parte de la rareza del mundo atómico, son los efectos cuánticos. Esta rareza proviene de la naturaleza de ondas y partículas duales de materia y energía.
Antes de estudiar física moderna, la mayoría de los estudiantes piensan a las partículas y ondas como categorías que pertenecen a diferentes objetos. Eso es comprensible, porque las partículas y las ondas tienen varias características diferentes, incluyendo la forma en que ocupan un lugar en el espacio, el modo en que viajan a través de aberturas y la masa o energía en sus interacciones.
Partículas. Estas existen en una cantidad bien definida en el espacio en algún instante de tiempo. Esta propiedad significa que las partículas están “localizadas”, ya que las partículas se encuentran en una coordenada determinada en un momento dado.
Ondas. Estas existen sobre una región extendida del espacio. Existen en forma de una función armónica (kx-wt) sobre los valores x de menos infinito a más infinito, sin distinguir un ciclo de otro. Así que, una onda de una sola frecuencia es inherentemente no localizada; existe en todas partes. Si se reduce el tamaño de una rendija por donde pasa una partícula, de modo que la longitud de onda sea más grande que la rendija, la onda se propaga expandiendo su efecto, se denomina difracción.
Interacción partículas y ondas. Las partículas interactúan con otras partículas en colisiones, y cuando las partículas chocan tienden a intercambiar impulso y energía. De acuerdo con las leyes de conservación, el impulso total y la energía total del sistema es el mismo antes y después, pero la energía y el impulso de cada objeto pueden cambiar como resultado de la colisión. Estas colisiones ocurren rápidamente, y este intercambio rápido es una cantidad discreta de energía e impulso, es un sello distintivo de las interacciones de partículas.
Las ondas, sin embargo, interactúan con otras ondas a través de la superposición en lugar de por colisiones. Cuando dos o más ondas ocupan la misma región del espacio, la onda resultante es la suma de todas las ondas contribuyentes. Se dice que las ondas interfieren entre sí, y si el resultado tiene mayor amplitud la interferencia es constructiva, y si la amplitud es menor, la interferencia es destructiva; todo esto depende de la contribución de fases relativas de las ondas superpuestas.
Las ondas también pueden interactuar con partículas, y tales interacciones parten de la energía de la onda que se puede transferir al objeto. A diferencia de la transferencia casi instantánea que ocurre en el choque de partículas, la transferencia de energía de una onda a un objeto ocurre durante un período prolongado de tiempo. La velocidad de transferencia de energía depende de las características de la onda.
Para comprender la dualidad onda-partícula, es útil considerar el tipo de experimento que podría realizar en una partícula para probar el comportamiento con ondas. Si un flujo de partículas que pasa por una rendija exhibe difracción, usted sabe que esas partículas se comportan como ondas. Sin embargo, para que la difracción sea significativa, el tamaño de la abertura debe ser comparable a la longitud de onda de la onda. Por lo tanto, eso significa que es necesario predecir la longitud de onda de las propiedades de la partícula.
Esa predicción es posible gracias al trabajo de Louis De Broglie, quien hipotetizó la existencia de ondas de materia en 1924. Casi dos décadas antes, Albert Einstein había demostrado que la luz exhibe características tanto de ondas como de partículas, comportándose como ondas al pasar a través de rendijas, pero actuando como partículas (llamados fotones) durante interacciones en el efecto fotoeléctrico. De Broglie hizo la inspirada suposición de que esta dualidad onda-partícula se extiende a electrones y otras partículas con masa.
Para entender la expresión de Broglie para la longitud de onda de una partícula, considere la relación de Einstein para la energía de un fotón con la frecuencia y longitud de onda:
![]()
Donde h es la constante de Planck (![]() ) y c es la velocidad de la luz. Aunque los fotones no tienen masa de reposo, llevan impulso, y la longitud de onda de ese impulso está relacionada con la energía del fotón:
) y c es la velocidad de la luz. Aunque los fotones no tienen masa de reposo, llevan impulso, y la longitud de onda de ese impulso está relacionada con la energía del fotón:
Por lo tanto, para un fotón, E=cp, y sustituyendo esto da:
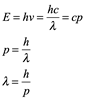
Si esta relación se mantiene también para las partículas con masa, entonces la longitud de onda de una partícula de masa m que viaja a la velocidad v es:
![]()
Ya que la magnitud del impulso de la partícula es p=mv.
Considerando las implicaciones de esta ecuación. Debido a que la longitud de onda y el impulso son inversamente proporcionales, la longitud de onda de una partícula aumenta a medida que disminuye el impulso de la partícula. Esta es la razón por la que solo las partículas en movimiento exhiben el comportamiento de onda: a velocidad cero, la longitud de onda se vuelve infinita a inconmensurable. Además, debido a que la constante de Planck es un número tan pequeño, el comportamiento de las ondas es medible solo cuando el impulso es lo suficientemente pequeño como para hacer que la fracción total h/p sea razonablemente grande. Por lo tanto, las características de onda de los objetos cotidianos no son evidentes porque su alta masa hace que sus longitudes de onda De Broglie sean demasiado pequeñas para medirlas.
Un humano de unos 75Kg, por ejemplo, su momento es de:
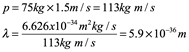
Esto no es solo miles de millones de veces más pequeño que el espacio entre átomos en un sólido típico, sino miles de millones de veces más pequeño que los protones y neutrones que componen los núcleos de los átomos. Por lo tanto, un objeto con masa de un humano no es un buen candidato para demostrar el comportamiento de onda de la materia. Sin embargo, para una masa muy pequeña con velocidad muy baja, la longitud de onda de Broglie puede ser lo suficientemente grande como para medirse, por ejemplo, para un electrón.
Ese experimento fue realizado por Clinton Davisson y Lester Germer en 1927. Sabiendo que las ondas difractadas de cristales producen un patrón de difracción. Descubrieron su hallazgo y buscaron evidencia de difracción. Luego, usaron los ángulos de dispersión y el espacio conocido de los átomos en el cristal para calcular la longitud de onda de los electrones. Sus resultados estuvieron en buen acuerdo con la expresión De Broglie para la longitud de onda de las partículas con la masa y la velocidad de los electrones utilizados en el experimento.
Entendiendo que los electrones pueden comportarse como ondas, es posible que te preguntes ¿Exactamente qué está ondulando? O, para preguntarlo de otra manera,¿por qué los electrones viajan como una onda e interactúan como una partícula? La respuesta proviene de la interpretación de la función de onda ![]() , solución a la ecuación de Schrödinger que gobierna las ondas de materia.
, solución a la ecuación de Schrödinger que gobierna las ondas de materia.
Aunque el gran físico Richard Feynman, dijo una vez que no es posible derivar la ecuación de Schrödinger de cualquier cosa que uno sepa, podemos tener una idea del razonamiento de Schrödinger comenzando con una expresión para la energía de una partícula. Si esa partícula se mueve no relativamente (es decir, lentamente en relación con la velocidad de la luz) y las fuerzas que actúan sobre la partícula son conservadas (de modo que una energía potencial puede estar asociada con cada fuerza), la energía mecánica total E de la partícula puede ser escrita como:
![]()
![]()
![]() Ec. 0
Ec. 0
Donde KE es la energía cinética y V es la energía potencial de la partícula. Puesto que los fotones podemos considerarlos (partículas de luz) con frecuencia asociada; tienen energía E=hv, Schrödinger escribió una versión de esta ecuación para la energía asociada con ondas de materia. Primero, debemos diferenciar a la constante de Planck h y la constante de Planck reducida ![]() , así como la relación de la frecuencia v con la frecuencia angular w:
, así como la relación de la frecuencia v con la frecuencia angular w:
![]()
![]()
![]()
![]()
Insertando esta expresión para la energía y usando p=mv, nos da:
![]()
![]()
La ecuación De Broglie relaciona el momento con la longitud de onda:
![]()
![]()
Podemos escribir:
![]() Ec. 1
Ec. 1
Para pasar de esta forma a la (ecuación de energía) ecuación de Schrödinger, suponemos que la onda de materia asociada con la partícula se puede escribir como la función de onda armónica ![]() :
:
![]()
![]() forma de fasor.
forma de fasor.
Observe que hemos dividido el exponencial para separar el término dependiente del tiempo del término dependiente del espacio. Eso hace que sea un poco más fácil tomar algunas derivadas que muestran cómo esta función de onda encaja Ec. 1:
La primera de esas derivadas es la de la relación ![]() con el tiempo t:
con el tiempo t:
![]()
![]() Ec. 2
Ec. 2
Enseguida, esas derivadas en relación a ![]() con x espacio:
con x espacio:
![]()
![]() Ec. 3
Ec. 3
Segunda derivada con respecto de x:
![]() Ec. 4
Ec. 4
El último paso antes de encajar estas derivadas en Ec. 2, es multiplicar por ![]() :
:
![]()
![]()
Ahora este resultado lo podemos conectar con la Ec. , igualando las ecuaciones:
![]()
![]()
Donde en la Ec. 4
![]()
![]() está sustituida en
está sustituida en ![]() en
en ![]()
Así que:
![]()
Para V=0
![]()
![]() Ec. 5
Ec. 5
Esta es la ecuación unidimensional dependiente del tiempo de Schrödinger. La ecuación de Schrödinger difiere con la ecuación de onda clásica en que la derivada parcial con respecto del tiempo es una primera en lugar de una segunda derivada, lo que tiene importantes implicaciones para la naturaleza de las soluciones. Tenga en cuenta también la presencia de “i” como factor multiplicativo, significa que las soluciones generales serán complejas.
Antes de considerar estas soluciones, debe tener en cuenta que es probable que encuentre una versión “independiente del tiempo” de la ecuación de Schrödinger. Puede derivar esa versión de la versión independiente del tiempo Ec. 2. y reemplazado la derivada del tiempo ![]() :
:
![]()
Si ![]()
![]() Ec. 6
Ec. 6
Desde ![]() , también puede verse esta ecuación escrita como:
, también puede verse esta ecuación escrita como:
![]() Ec. 7
Ec. 7
![]() Ec. 8
Ec. 8
Es importante que tenga en cuenta, que la etiqueta “independiente del tiempo”, no significa que la función de onda ![]() , no es una función del tiempo en Ec. 8. Antes de sumergirnos en las soluciones a la ecuación de Schrödinger, piense en el significado Ec. 8. Es esencialmente una expresión de la conservación de la energía. La energía total menos la energía potencial es igual a la energía cinética. Así que Ec. 8 nos dice que la energía cinética de la partícula es proporcional a la segunda derivada de
, no es una función del tiempo en Ec. 8. Antes de sumergirnos en las soluciones a la ecuación de Schrödinger, piense en el significado Ec. 8. Es esencialmente una expresión de la conservación de la energía. La energía total menos la energía potencial es igual a la energía cinética. Así que Ec. 8 nos dice que la energía cinética de la partícula es proporcional a la segunda derivada de ![]() , que es la curvatura de la función de onda. Una mayor curvatura con x significa que la forma de onda tiene una frecuencia espacial más alta (va de positiva a negativa en una distancia más corta), lo que significa que tiene una longitud de onda más corta y la ecuación De Broglie relaciona la longitud de onda más corta con el impulso más alto.
, que es la curvatura de la función de onda. Una mayor curvatura con x significa que la forma de onda tiene una frecuencia espacial más alta (va de positiva a negativa en una distancia más corta), lo que significa que tiene una longitud de onda más corta y la ecuación De Broglie relaciona la longitud de onda más corta con el impulso más alto.
5.2 Ecuación de Schrödinger
¿Cuál es la ecuación de Schrödinger independiente del tiempo para una partícula libre?
En este contexto, “libre” significa que la partícula está libre de la influencia de las fuerzas externas, y dado que la fuerza es el gradiente de la energía potencial, una partícula libre viaja en una región de energía potencial constante. Dado que la ubicación de referencia de la energía potencial es cero arbitrario, puede establecerse que V=0 en la ecuación de Schrödinger para una partícula libre. Así que Ec. 7 se convierten en:
![]() Ec. 9.
Ec. 9.
Despejar la segunda derivada de la función de onda:
![]() Ec. 10
Ec. 10
Dado que la energía total de una partícula es igual a energía cinética de la partícula, se puede establecer:
![]() sustituir en Ec. 10
sustituir en Ec. 10
![]() Ec. 11
Ec. 11
Esta es la ecuación de Schrödinger para una partícula libre. Es instructivo comparar esta ecuación con la de la onda:
![]()
Que es casi idéntica a Ec. 11, siempre que:
![]()
Pero el número de onda ![]()
![]()
![]()
![]()
Resolviendo para lambda ![]() :
:
![]()
Que es la expresión De Broglie para la longitud de onda de una onda de materia. Para una partícula libre, la frecuencia de oscilación y la energía pueden tomar cualquier valor, pero las partículas en regiones en las que varía la energía potencial pueden estar limitadas a ciertos valores de frecuencia y energía que dependen de las condiciones límite. Por tanto, las energías permitidas de una partícula en un pozo potencial se cuantizan. Esto significa que la característica de onda de una partícula es análoga a una onda estacionaria, y la energía de la partícula es proporcional a la frecuencia de oscilación de esa onda estacionaria. Es posible que veamos a la ecuación de Schrödinger “independiente del tiempo” como estados estacionarios, pero debe tener en cuenta que esto significa solo que la energía del sistema es constante sobre el tiempo, no es que la función de onda esté estacionaria.
Cuando escribió por primera vez su ecuación Schrödinger, no sabía lo que representaba físicamente la función de onda ![]() ; intuyó que era la densidad de carga del electrón. Esta es una suposición razonable, ya que estaba escribiendo una ecuación para seguir a los electrones, y a medida que los grupos de electrones se extienden a través del espacio, se puede evaluar la cantidad de carga por volumen de unidad (la densidad de carga), como una forma de saber dónde se congregan los electrones. Sin embargo, Max Born pudo demostrar que este punto de vista es incompatible con los experimentos y ofreció su propia explicación, que ahora es el entendimiento moderno.
; intuyó que era la densidad de carga del electrón. Esta es una suposición razonable, ya que estaba escribiendo una ecuación para seguir a los electrones, y a medida que los grupos de electrones se extienden a través del espacio, se puede evaluar la cantidad de carga por volumen de unidad (la densidad de carga), como una forma de saber dónde se congregan los electrones. Sin embargo, Max Born pudo demostrar que este punto de vista es incompatible con los experimentos y ofreció su propia explicación, que ahora es el entendimiento moderno.
La interpretación moderna de la función de onda, es que es una "amplitud de probabilidad", relacionada con la probabilidad de encontrar la partícula en una región determinada del espacio. Esta cantidad se llama amplitud porque, así como debe encuadrar la amplitud de una onda mecánica para obtener su energía, por ello debe encuadrar la función de onda para obtener densidad de probabilidad P. Puesto que la función de onda es generalmente compleja, los cuadrados multiplicados por su complejo conjugado:
![]()
O
![]()
En una dimensión la densidad de probabilidad, es la probabilidad por longitud de unidad, en dos dimensiones es la probabilidad por área de unidad, y en tres dimensiones es la probabilidad por unidad de volumen. En otras palabras, P(x,t) le indica cómo la probabilidad de encontrar la partícula en un lugar determinado se extiende por el espacio en un momento dado.
Esto responde a la pregunta de lo que está perturbando un electrón y otros objetos cuánticos: una partícula viajera es en realidad un paquete itinerante de amplitud de probabilidad. Cuando se encuentra con un obstáculo como la doble ranura descrita en el experimento del mismo nombre; la amplitud de probabilidad se difracta de acuerdo con la longitud de onda. Cuando interactúa, esta función de onda se contrae al resultado único medido.
Este resultado es discreto, es consistente con el comportamiento de las partículas (como los puntos individuales que aparecen en el detector en la versión de electrones del experimento de doble ranura). Entonces, ¿cómo podemos escribir la función de onda para una partícula libre? Antes usamos una conjetura inicial de la compleja función armónica:
![]() (1.0)
(1.0)
Que es la combinación de una onda coseno y seno, como se muestra al principio de este apartado. Pero surge un problema cuando intenta calcular la probabilidad de encontrar la partícula en algún lugar del espacio usando esta forma de onda. Puesto que ![]() representa la densidad de probabilidad, la integración en todo el espacio
representa la densidad de probabilidad, la integración en todo el espacio ![]() debe dar una probabilidad de uno, ya que la posibilidad de encontrar la partícula en algún lugar en el espacio es del 100%). Sin embargo, utilizando la función de onda, esa integración se ve así:
debe dar una probabilidad de uno, ya que la posibilidad de encontrar la partícula en algún lugar en el espacio es del 100%). Sin embargo, utilizando la función de onda, esa integración se ve así:
![]()
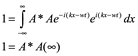
Puesto que nada puede multiplicarse por infinito para dar uno, esta forma de onda es “no normalizada” (se refiere al proceso de escalar la función de onda para establecer la probabilidad de encontrar la partícula en algún lugar en el espacio al 100%). Para modificar la función de onda de (1.0) para hacerla normalizable, los conceptos de Fourier necesarios.
Paquetes de onda cuánticos
Una partícula está localizada en el espacio, por lo que parece razonable esperar que su onda también debe ser espacialmente limitada; es decir, debe ser un paquete de onda en lugar de una onda de longitud de onda única con amplitud constante en todo el espacio. Este paquete de ondas debe estar dominado por una longitud de onda particular (o impulso) para que la hipótesis De Broglie sea todavía más o menos aplicable. Es imposible formar un paquete de onda sin incluir cierta cantidad de ondas con diferentes longitudes de onda. Un rango de diferentes longitudes de onda significa un rango de números de onda (![]() ), y rango de números de ondas significa un rango de momento
), y rango de números de ondas significa un rango de momento ![]() . Por lo tanto, el desafío es hacer un paquete de ondas que se localice en el espacio sobre una región, pero, que viaje con un impulso bien definido
. Por lo tanto, el desafío es hacer un paquete de ondas que se localice en el espacio sobre una región, pero, que viaje con un impulso bien definido ![]() , donde
, donde ![]() representa el número de onda dominante.
representa el número de onda dominante.
Tal función de onda ![]() , depende tanto de la ubicación x y el tiempo t, pero es un poco más fácil ver lo que está pasando separando las variables, escribiendo
, depende tanto de la ubicación x y el tiempo t, pero es un poco más fácil ver lo que está pasando separando las variables, escribiendo ![]() como
como ![]()
![]() le permite concentrarse en localizar el término espacial; el efecto del término de tiempo
le permite concentrarse en localizar el término espacial; el efecto del término de tiempo ![]() . Un enfoque para limitar la extensión de la función de onda es escribir como el producto de dos funciones:
. Un enfoque para limitar la extensión de la función de onda es escribir como el producto de dos funciones:
![]() si la función va a cero en todas partes excepto en cierto rango de valores x, entonces las oscilaciones del paquete de onda se localizan en ese rango.
si la función va a cero en todas partes excepto en cierto rango de valores x, entonces las oscilaciones del paquete de onda se localizan en ese rango.
Ahora considere la función sobre g(x) dada por la ecuación:
![]()
 21.52.52.png)
Esta función alcanza un pico en g(x)=1 con x=0 y disminuye hacia cero en ambas direcciones a una velocidad determinada por el valor de la constante a.
La función envolvente g(x) por la función oscilante (x) hace que la función del producto g(x)(f(x)) se deshaga tanto en la dirección negativa como en la dirección positiva.
 21.53.02.png)
Desde ![]() y
y ![]() , la función de onda
, la función de onda ![]() y la conjugada
y la conjugada ![]() son:
son:
![]()
Por lo que la densidad de probabilidad es
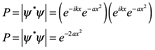
Integrando esto para todo el espacio
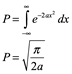
Por lo tanto, para todo el espacio P=1, tendremos que escalar ![]() para la inversa de este factor. Esto significa que debe ser escalada para la raíz cuadrada su inversa,
para la inversa de este factor. Esto significa que debe ser escalada para la raíz cuadrada su inversa, ![]() así que:
así que:
![]()
Esta función tiene las características deseadas de extensión espacial limitada, mientras oscila a una longitud de onda dominante, y se normaliza para dar una probabilidad de uno para todo el espacio.
Ejemplo: determine la probabilidad de encontrar una partícula en una ubicación determinada si la función de onda de la partícula se define como:
![]()
En este caso, la constante de anchura a=0.1, lo que hace que la densidad de probabilidad:
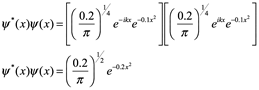
La distribución Gaussiana, como se muestra para
![]()
 22.54.23.png)
Para encontrar la probabilidad de que la partícula con esta función de onda se encuentre en un punto particular, tenemos que integrar la densidad alrededor de ese lugar. En este ejemplo, la probabilidad de encontrar la partícula en x=1m, con desviación de 0.1m, es
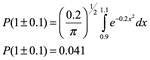
Puede comprobar la normalización de esta función integrando en todo el espacio:
![]()
Así que, la probabilidad de encontrar esta partícula en algún lugar en el espacio es de hecho 100%.