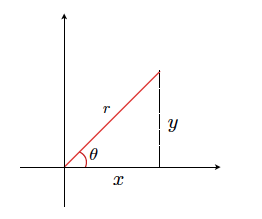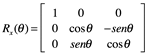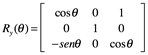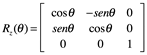Campos vectoriales
Y teoría electrostática
Unidad 1.
El espacio vectorial
Hay muchas maneras de introducirnos en el tema de los vectores, ese objeto que es una representación matemática de una entidad física que puede ser caracterizado por el tamaño o magnitud, y la dirección. En consecuencia, con esta definición se puede emplear para representar cantidades vectoriales por ejemplo velocidad, posición, fuerza. El propósito de aprendizaje de este objeto matemático, es introducirnos en la comprensión de vectores y tensores, dado que son ampliamente utilizados en aplicaciones avanzadas en la tecnología moderna. El antecedente a estos conceptos usted lo recibió en la educación secundaria. En ese nivel seguramente aprendió que los vectores son cantidades con magnitud y dirección, al sumarlos gráficamente, además de calcular sus componentes en las direcciones x-y-z.
El propósito es tratar con vectores desde una perspectiva desde el álgebra, derivadas vectoriales, sistemas de coordenadas y sus implicaciones en los tensores gradiente, divergente, rotor, laplaciano en el marco de la teoría electrostática.
Habilidades de aprendizaje:
1. Dominará el álgebra de vectores y su notación
2. Definirá sistema de coordenadas
3. Realizará transformaciones de sistemas de coordenadas
4. Realizará operaciones de productos vectoriales
5. Definirá y realizará operaciones con tensores: gradiente, divergente, rotor y laplaciano.
1.1 Magnitud escalar
Si tenemos un número real y una unidad de medida, por ejemplo, 4 m; 2 s; 5 kg; estamos frente a magnitudes escalares. Un número escalar es un número real, constante o complejo que nos expresa alguna magnitud física. Matemáticamente al conjunto de escalares se le llama cuerpo, campo o anillo. Un cuerpo o campo es el conjunto cerrado bajo una operación binaria de suma y multiplicación, en las que cumple con todas la propiedades de un álgebra como la aritmética.
La álgebra es un campo asombrosamente dinámico en su cambio, los estudiantes generalmente tienden a expresar por álgebra a las operaciones con polinomios, resolver sus ecuaciones hasta tercer grado y realizan cálculos de determinantes, reducciones de expresiones racionales y el estudio de las curvas asociadas a estos polinomios, la reconocen en libros de pre-cálculo. Aunque en nuestros días, la álgebra computacional gana enormes aplicaciones, se le suele marginar de ser un elemento de matemática elemental. Definir una álgebra como un cuerpo o campo cerrado bajo una operación binaria, es referirnos a ella de manera formal. Una álgebra aritmética es hecho su cuerpo de números reales, una álgebra arábiga de polinomios, una compleja de números complejos, una integral de familia de funciones, una lineal de matrices,…, a todas ellas se les identifica por cumplir con alguna estructura de axiomas tales como la conmutativa, la asociativa, la distributiva, el elemento neutro y el inverso simétrico. En consecuencia todos los ejercicios algebraicos se desprenden de estos axiomas:
El objeto de aprender cualquier álgebra, por error se confunde en la educación como resolver miles y miles de ejercicios, como un modo de comprenderlo como un sistema de axiomas de cerradura, es decir, que encapsulan cualquier resultado dentro de su propio cuerpo o campo. Los axiomas suelen ser estos últimos nueve citados en líneas atrás. El error es que los estudiantes suelen quedarse solo en ejercicios y dejan de ver el panorama del poder de estos sistemas axiomáticos, o comúnmente en la matemática formal se les llama campos o cuerpos. En cuanto algo cumple con estos nueve axiomas se le llama campo, y la teoría de campos es la rama que estudia a las álgebras. El primer campo que conocemos esta hecho de números reales, el segundo de polinomios, el tercero de complejos, el cuarto de funciones, el quinto de vectores, el sexto de matrices,…, y cada uno es un terreno único en sus posibilidades científicas y tecnológicas.
En el siglo XX se desarrollaron muchos sistemas encapsulados en apoyo computacional a la criptografía comercial, militar y científica. El dinero electrónico y las transacciones comerciales en la Internet no pueden ser posibles sin este robusto cuerpo de conocimiento. Es cierto que no todas las álgebras cumplen con los nueve axiomas ya referidos, este problema escapa a la intención de este texto, pero téngalo presente, las matemáticas modernas casi todo lo refieren a estos sistemas axiomáticos. ¿Quién hubiera pensado que casi todo el vasto mundo de las matemáticas es desprendido de estos axiomas básicos?
Pero hay otras estructuras algebraicas, por ejemplo, si una álgebra no cumple con el axioma del elemento inverso simétrico ![]() llamaremos a ese campo anillo (permite la existencia de fracciones, el producto en un anillo no necesariamente tiene operaciones inversas). El primer anillo que todos conocemos es el sistema de números enteros. Los números naturales (enteros positivos) no son un campo ni anillo. No queda muy claro porqué los números racionales y enteros
llamaremos a ese campo anillo (permite la existencia de fracciones, el producto en un anillo no necesariamente tiene operaciones inversas). El primer anillo que todos conocemos es el sistema de números enteros. Los números naturales (enteros positivos) no son un campo ni anillo. No queda muy claro porqué los números racionales y enteros ![]() , son más útiles que los naturales, puesto que todas las propiedades de los números enteros o racionales se heredan de los enteros positivos. Quizá la razón sea que tienen mejor estructura algebraica en su cuerpo axiomático, en algún sentido. El anillo parece ser un buen escenario para discutir temas como la divisibilidad y los números primos, mientras que la estructura del campo es buena en geometría.
, son más útiles que los naturales, puesto que todas las propiedades de los números enteros o racionales se heredan de los enteros positivos. Quizá la razón sea que tienen mejor estructura algebraica en su cuerpo axiomático, en algún sentido. El anillo parece ser un buen escenario para discutir temas como la divisibilidad y los números primos, mientras que la estructura del campo es buena en geometría.
Campo escalar: representa un espacio distribuido de magnitudes escalares. El campo escalar es una función escalar que define un único número, coordenada o variable escalar. Un escalar es un tensor de rango cero.
Ejemplo: dada la función escalar de temperatura ![]() construyamos parte del espacio escalar con ayuda de una tabla de evolución:
construyamos parte del espacio escalar con ayuda de una tabla de evolución:
 10.49.48.png)
1.2 Magnitud vectorial
Las magnitudes vectoriales extienden las dimensiones escalares asociadas a dirección y sentido. Históricamente un vector surge de la idea del irlandés William Hamilton, con el nombre de cuaterniones, son la extensión del plano complejo al espacio, creando nuevas interpretaciones de la realidad física[1]. Pero es Lord Kelvin quien resuelve los problemas con el manejo de los cuaterniones separando la parte real y la imaginaria, originando con ello los espacios vectoriales y su análisis dado por Grassmann[2], es así como nace la era vectorial. En un libro histórico de Michael J. Crowe titulado Una Historia del análisis vectorial y que pronto se convirtió en un libro casi obligado en las ingenierías y escuelas[3] de ciencias de 1967. Sin duda las tensiones entre algebristas y geómetras encuentran su reconciliación en el análisis vectorial en 1831, surge como consecuencia de la creación y representación de los números complejos; resultado de la investigación de Leibniz de una geometría de posición y por la idea de un paralelogramo de fuerzas o velocidades. A Jerome Cardan (1545) se le atribuye la publicación del número complejo, este concepto tardó dos siglos en ser legitimado por la comunidad matemática. Ya en 1679 Christiaan Huygens, Gottfried Wilhelm Leibniz crean la idea de una matemática que exprese directamente como álgebra magnitudes en el espacio geométrico, algo similar al análisis vectorial. Es el gran Isaac Newton quien en 1687 introduce en su Principia Mathematica, un cuerpo actuado por dos fuerzas simultáneamente, se describirá con la diagonal de un paralelogramo al mismo tiempo que son descritas las dos fuerzas por separado, esta idea es muy próxima al concepto de vector. En 1799 el noruego Caspar Wessel expone la representación geométrica de los números complejos, con ello inaugura la representación analítica dirección. Al mismo tiempo, Carl Friedrich Gauss busca el manejo de cantidades en el espacio tridimensional.
Grassmann y Hamilton se enteran en 1852 sobre los avances de Gauss, Hamilton publica en 1853 Lectura de cuaterniones. Hamilton no estuvo solo en la creación del análisis vectorial, estaban August Ferdinand Möbius, Giusto Bellavitis, el conde de Saint-Venant, Augustin Cauchy, Matthew O'Brien, y sobre todo, Hermann Günther Grassmann. Giusto Bellavitis publica su idea de equipolente: "Dos líneas rectas se llaman equiparadas si son iguales, paralelas y dirigidas en el mismo sentido” sus líneas de hecho se comportan exactamente de la misma manera que los números complejos, pero es importante tener en cuenta que él consideraba sus líneas como entidades esencialmente geométricas, no como representaciones geométricas de las entidades algebraicas, de hecho, él se opuso a los números complejos como "indigno de pertenecer a una ciencia basada en la razón." Bellavitis dedicó un largo periodo en un fallido intento de extender su sistema a tres dimensiones. Grassmann pone los cimientos de los productos cruz y punto vectorial, el inglés Matthew O’Brien en 1852 es quien publica un sistema de análisis vectorial desarrollado a partir de los cuaterniones de Hamilton, no logrando la propiedad asociativa de entidades vectoriales. Alrededor de 1880, el moderno sistema de análisis vectorial llegó a existir a través de la obra de Josiah Willard Gibbs y Oliver Heaviside, y para 1910 se había establecido como el sistema dominante. En 1867 nace el operador Nabla:
![]()
empleado con éxito por James Clerke Maxwell. Pero es Josiah Willard Gibbs quien introduce la notación moderna del análisis vectorial, funciones vectoriales y encuentra un eco importante en la física electromagnética de Maxwell.
Sin duda la geometría ingresa con fuerza en las matemáticas con el teorema de Pitágoras. Este teorema afirma que el cuadrado debajo de la hipotenusa c de un triángulo rectángulo es igual (en área) a la suma de los cuadrados de los otros dos lados.
 13.24.30.png)
 13.44.31.png)
Fuente: https://es.wikipedia.org/wiki/Teorema_de_Pitágoras
El teorema es apenas obvio, la prueba se muestra arriba en la figura, las mitades de los rectángulos del cuadrado perfecto formado en completo a los cuadros por a y b, justo por la mitad es igual a un corto cuadro grande menos cuatro copias del triángulo referido. La respuesta a los axiomas de Euclides en su libro Elements, se consolida con el teorema de Pitágoras. Este enfoque, hace unos 100 años, los matemáticos consideran que el rigor y universalidad del sistema de axiomas Euclidiano no rellena algunos huecos vacíos de la geometría. El requerir una gran cantidad de nuevos axiomas adicionales y el hecho que hay otra geometría que requieren modificar el sistema de axiomas.
 13.51.13.png)
Nos parece que el enfoque axiomático debe ser abandonado en la geometría y esta debe basarse en el enfoque algebraico iniciado por Descartes en el siglo XVII. En geometría algebraica, los puntos en el plano se dan por pares ordenados (x,y) números y líneas curvas son expresadas por ecuaciones polinómicas en x y y. Desde el punto (x,y) se encuentra la distancia horizontal x y la vertical y desde el origen O. Nosotros definimos la distancia como:
![]()
motivado por el teorema de Pitágoras.
Un círculo de radio unidad, que consiste en los puntos a distancia 1 hasta O. Tiene la ecuación
![]()
Mas generalmente, el círculo con centro en (a,b) y radio r tiene la ecuación
![]()
El problema con este enfoque algebraico es que va demasiado lejos, no hay ninguna restricción natural en las ecuaciones que precise los conceptos geométricos de Euclides. Si nos detenemos en estas ecuaciones lineales obtenemos solamente líneas; si lo hacemos para las cuadráticas obtenemos todas las cónicas, hipérbolas, elipses y parábolas. Mientras que con Euclides solo círculos. Sin embargo, hay un concepto algebraico diferente que surge, y que refiere a un lugar en el espacio geométrico: el concepto de vector, y nuevos productos tales como el producto interno y el cruz. Si bien no da la generalidad del espacio vectorial, en su lugar describe el espacio vectorial ![]() que es convenientemente para la geometría plana euclidiana. Este espacio cita a todos los pares ordenados (x,y) donde x y y pertenece a los
que es convenientemente para la geometría plana euclidiana. Este espacio cita a todos los pares ordenados (x,y) donde x y y pertenece a los ![]() , el conjunto de los números reales.
, el conjunto de los números reales.
Se nos permite agregar una nueva regla:
![]()
Y para multiplicar un par por cualquier número real c utilizamos la regla de:
![]()
Estas operaciones tienen interpretación geométrica natural: adición ![]() a cada
a cada ![]() , significa trasladar el plano; es decir, cambiando todos sus puntos a través de la distancia horizontal a y distancia b vertical. Multiplicando cada
, significa trasladar el plano; es decir, cambiando todos sus puntos a través de la distancia horizontal a y distancia b vertical. Multiplicando cada ![]() por el factor c, aumenta el plano entero por el factor c. Como veremos este ajuste simple prueba algunos teoremas geométricos interesantes. Pero para capturar todos los de la geometría de Euclides tenemos un ingrediente adicional: el producto interno, llamado también producto punto, definido por
por el factor c, aumenta el plano entero por el factor c. Como veremos este ajuste simple prueba algunos teoremas geométricos interesantes. Pero para capturar todos los de la geometría de Euclides tenemos un ingrediente adicional: el producto interno, llamado también producto punto, definido por
![]()
Note que:
![]()
Donde ![]() denota la distancia de (x,y) dede el origen O. Por lo tanto, el producto interno puede ser definido como la distancia de acuerdo con el teorema de Pitágoras. Una vez que tenemos el concepto de distancia, también podemos obtener el concepto de ángulo, porque resulta que
denota la distancia de (x,y) dede el origen O. Por lo tanto, el producto interno puede ser definido como la distancia de acuerdo con el teorema de Pitágoras. Una vez que tenemos el concepto de distancia, también podemos obtener el concepto de ángulo, porque resulta que
![]()
Donde ![]() es el ángulo entre
es el ángulo entre
![]()
Como se muestra enseguida:
 14.36.11.png)
Las principales ventajas de utilizar el concepto de un espacio vectorial con el producto interno, en lugar de los axiomas de Euclides, son la familiaridad y universalidad. Las reglas para calcular los vectores son similares al álgebra tradicional; también, el producto interno y los espacios vectoriales ocurren en muchas partes de las matemáticas, por lo que vale la pena aprender como herramienta de uso general. En resumen, hay otras geométrias distintas a la Euclidiana, por ejemplo la hiperbólica en la que el postulado de las rectas paralelas de Euclides es falso, los ángulos de un triángulo nos suman pi y para una figura de un tamaño dado, no existe otra semejante de tamaño mayor.

1.3 El vector en![]()
El vector se expresa como una cantidad que tiene tanto magnitud como dirección; geométricamente es referido como un segmento de línea dirigido (con sentido dado por una flecha) expresado por símbolos en cursivas, en negritas o con una flecha por encima:
![]()
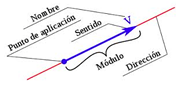
Un vector v, tiene un punto de origen en C y cuyo punto de aplicación o destino es D, se expresa como ![]() . Su magnitud está dada por norma o módulo del vector v,
. Su magnitud está dada por norma o módulo del vector v,
![]() , como la raíz cuadrada de sus componentes espaciales. Diremos que dos vectores son iguales si tienen la misma magnitud y dirección,
, como la raíz cuadrada de sus componentes espaciales. Diremos que dos vectores son iguales si tienen la misma magnitud y dirección, ![]() o
o ![]() .
.
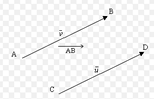
Es importante tener en cuenta que los vectores son libres de moverse en el espacio geométrico de un punto a otro, sin modificar magnitud y dirección, con ello facilita el cálculo algebraico en el espacio geométrico. Si cambia el sentido, pero no la magnitud y dirección, tenemos un vector negativo![]() , si lo multiplicamos por un escalar diferente de cero p, obtenemos un vector de misma dirección y magnitud p veces,
, si lo multiplicamos por un escalar diferente de cero p, obtenemos un vector de misma dirección y magnitud p veces, ![]() . El vector cero es un vector de cualquier dirección de magnitud cero.
. El vector cero es un vector de cualquier dirección de magnitud cero.
La adición de vectores. Los vectores pueden compartir o no un punto común de inicio, o pueden desplazarse de manera paralela para calcular la suma de ellos, y encontrar un vector resultante, ![]() .
.
El vector resultante puede verse como la diagonal principal de un paralelogramo. Es más común trabajar con la versión analítica de los vectores, de una forma algebraica. La notación de un vector es:
![]()
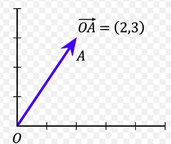
donde ![]() son componentes del vector v. Por ejemplo, cuando un vector inicia en vector cero y termina en el punto P (2,3), se llama vector de posición
son componentes del vector v. Por ejemplo, cuando un vector inicia en vector cero y termina en el punto P (2,3), se llama vector de posición ![]()
Adición de vectores, método analítico
Dados los vectores:
![]()
![]()
Ejemplo:
![]()
la suma es:
![]()
la resta ![]() es:
es:
![]()
Multiplicación de vectores por un escalar, método analítico
La multiplicación de un vector![]() por un escalar p diferente, es:
por un escalar p diferente, es:
![]()
Ejemplo:
![]() y por el escalar p=3
y por el escalar p=3
![]()
Dos vectores son iguales ![]() si y solo sí,
si y solo sí, ![]() y
y ![]()
1.4 Producto interno/punto
El producto punto, producto interno o producto escalar de dos vectores es un escalar dado por
![]()
![]()
Se expresa como
![]()
Propiedades del producto interno
|
|
Si los vectores son ortogonales, el producto interno de ellos es cero |
|
|
Conmutativo |
|
|
Distributivo |
|
|
Al elevar al cuadrado un vector, también lo hace de la misma manera su módulo o norma. |
Ejemplo:
![]()
![]()
Representa la proyección de la magnitud de la sombra de ![]() sobre
sobre ![]() . Otro camino es calcular el producto punto con la magnitud de los vectores y el ángulo entre ellos.
. Otro camino es calcular el producto punto con la magnitud de los vectores y el ángulo entre ellos.
![]()
El ángulo de un vector![]() en
en ![]() , es dado por:
, es dado por:
 19.00.48.png)
Nota: El resultado es aproximado porque las raíces nos dan decimales infinitos.
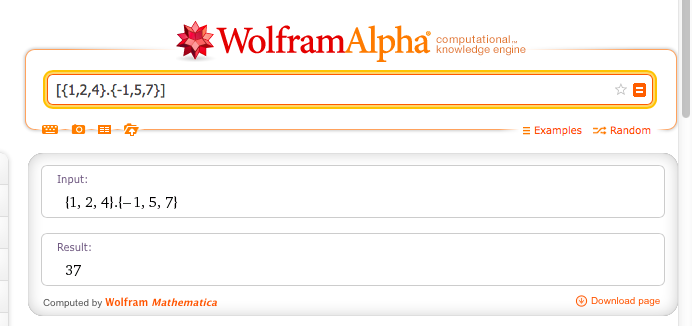
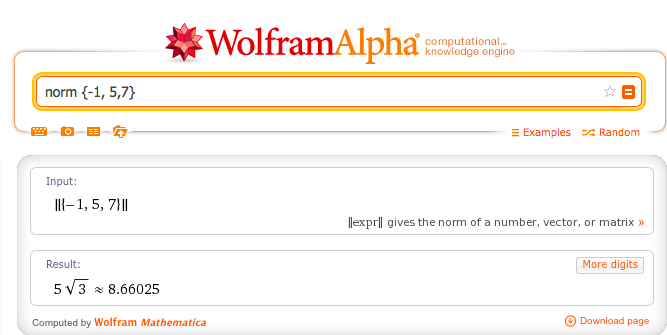
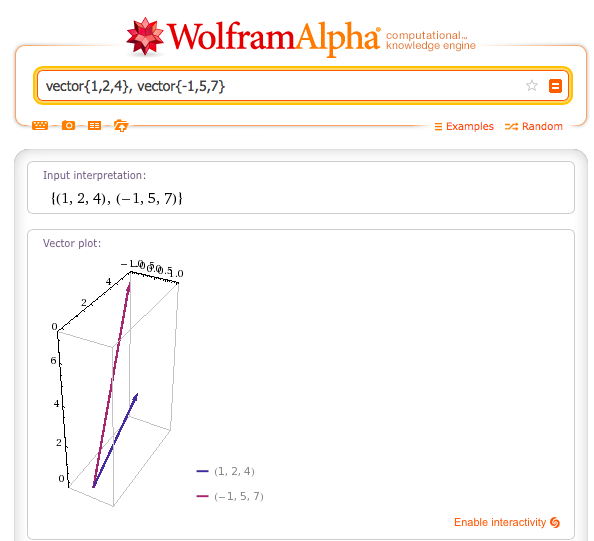
Con ayuda de Wolfram alpha (http://www.wolframalpha.com) un vector se introduce así como lo indica la siguiente imagen para saber su información. Por ejemplo para nuestros vectores anteriores v y u.




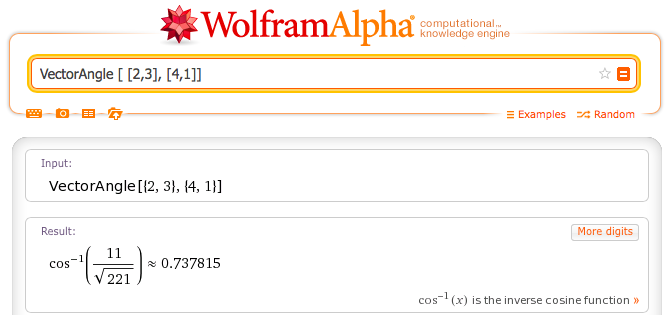
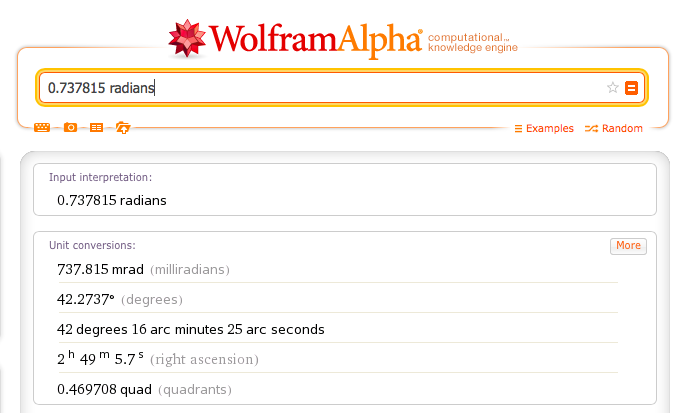
Son 42.2737º entre los vectores.
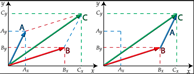
Al método del paralelogramo también se le conoce como método de triángulos y polígonos por descomposición de componentes rectangulares. Dados dos puntos
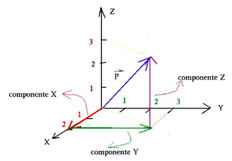
En papel cuadriculado dibujamos los vectores posición
Puede verse que el vector ![]()
es igual al vector ![]()
por tener la misma magnitud y dirección.
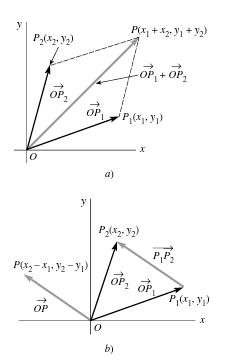
Dado que los vectores son magnitudes que responden a un álgebra, sus propiedades son
 11.18.10.png)
Inspeccionar: http://demonstrations.wolfram.com/3DVectorDecomposition/
1.5 El vector en ![]()
La norma, módulo o magnitud de un vector en ![]() , es dada por:
, es dada por:
![]()
En el espacio ![]() , es común trabajar los vectores en términos de vectores unitarios, son vectores de magnitud 1, dirección sobre los ejes x,y,z respectivamente, se les llama
, es común trabajar los vectores en términos de vectores unitarios, son vectores de magnitud 1, dirección sobre los ejes x,y,z respectivamente, se les llama ![]() . Estos vectores
. Estos vectores ![]() unitarios se les llama base de un sistema tridimensional. Además, de cualquier vector podemos obtener su vector unitario, de la siguiente manera:
unitarios se les llama base de un sistema tridimensional. Además, de cualquier vector podemos obtener su vector unitario, de la siguiente manera:
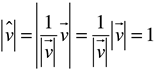
Ejemplo, para el vector ![]() genere un vector unitario en la dirección de
genere un vector unitario en la dirección de ![]() y otro en la opuesta.
y otro en la opuesta.
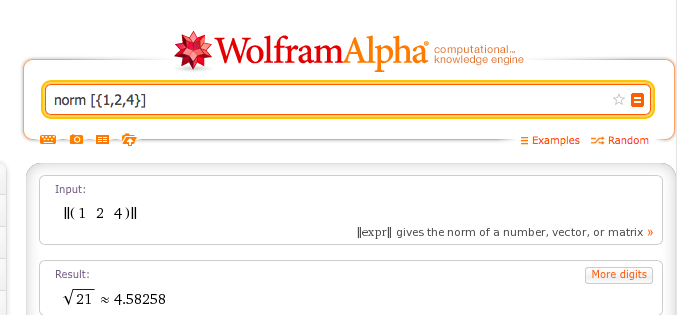
Solución. La norma de
![]()

Entonces el vector unitario en la misma dirección es
![]()
El vector unitario en la dirección contraria es
![]()
Los vectores unitarios ![]() , son los vectores que sobre los ejes de coordenadas se forman con una esfera de radio uno. Es una forma alternativa para trabajar los componentes de un vector.
, son los vectores que sobre los ejes de coordenadas se forman con una esfera de radio uno. Es una forma alternativa para trabajar los componentes de un vector.
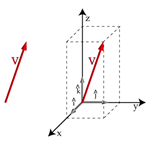
La representación de vectores en ![]() , es escribir un vector asociado a sus coordenadas relativas a los tres ejes mutuamente ortogonales y al origen dado por el vector cero. Formándose los planos xz, yz, xy. Con estos planos coordenados podemos referir cualquier vector en
, es escribir un vector asociado a sus coordenadas relativas a los tres ejes mutuamente ortogonales y al origen dado por el vector cero. Formándose los planos xz, yz, xy. Con estos planos coordenados podemos referir cualquier vector en ![]() , dependiendo del octante en el que actúa (8 partes conocidas en
, dependiendo del octante en el que actúa (8 partes conocidas en![]() ). Por ejemplo, el octante donde las tres componentes de un vector son positivas se llama primer octante.
). Por ejemplo, el octante donde las tres componentes de un vector son positivas se llama primer octante.
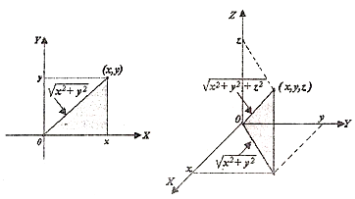
Las coordenadas de un punto en ![]() , coinciden con las componentes de un vector posición en
, coinciden con las componentes de un vector posición en ![]()
Dado un vector en términos de vectores unitarios:
![]()
Las propiedades de los vectores en ![]() , son las mismas que para
, son las mismas que para ![]() .
.
Ejemplo. Calcule la distancia entre los vectores de posición y el ángulo entre ellos:
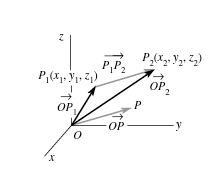
![]()
Solución. Calculemos el vector que une las dos cabezas de vector
![]()
![]()
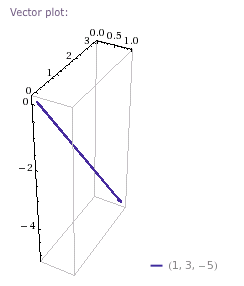
Este vector [-2,3,3] se puede dibujar saliendo del origen o desde el punto. La distancia entre las dos cabezas de vector corresponde a
![]()
Ángulo entre los dos vectores de posición en el espacio, usaremos el producto punto
![]()
entonces:
 19.19.37.png)
1.6 Producto cruz de vectores
El producto cruz de dos vectores en ![]() , es dado por Gibbs, como un vector perpendicular al plano formado por los vectores dentro de un producto vectorial.
, es dado por Gibbs, como un vector perpendicular al plano formado por los vectores dentro de un producto vectorial.
![]()
Donde ![]() , es un vector unitario perpendicular al plano formado por los vectores multiplicados. Usando la notación
, es un vector unitario perpendicular al plano formado por los vectores multiplicados. Usando la notación ![]() y empleando determinantes:
y empleando determinantes:
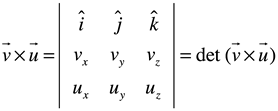
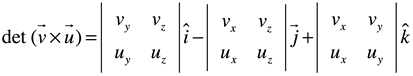
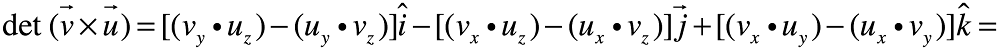
Ejemplo: Determine el producto vectorial entre
![]()

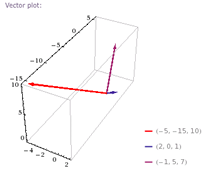
Verifique usted
![]()
Propiedades de producto cruz
|
|
No es conmutativo |
|
|
Distributivo |
|
|
Donde c es un escalar |
|
|
El producto cruz de dos vectores es cero si son vectores paralelos |
1.7 Magnitud tensorial
Es la relación de fusión de los elementos algebraicos escalar, vectorial y matricial. Tensor se refiere a un campo tensorial. El tensor es un concepto que agrupa los ya mencionados objetos escalar, vectorial y matricial, con propia notación y que provocó una nueva manera de pensar las leyes físicas dentro del electromagnetismo, mecánica de fluidos, teoría de la elasticidad, geometría diferencial y el álgebra lineal. Es un concepto que hace especial atención entre magnitudes físicas o geométricas. El espacio vectorial es la estructura matemática para el desarrollo del álgebra tensorial. La física moderna descansa sobre este importante concepto de tensor, por limitaciones en el alcance de este curso, no profundizaremos más sobre este fascinante mundo tensorial.
1.8 Sistemas de coordenadas
En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema. Las líneas de intersección de las superficies coordenadas se llaman curvas coordenadas y son ortogonales entre sí.
Los vectores unitarios tangentes a las curvas coordenadas son mutuamente ortogonales y coinciden con los vectores unitarios perpendiculares a las superficies coordenadas. Estos vectores forman una base que permite representar cualquier vector en función de sus componentes en el sistema de coordenadas:
![]()
En general, las coordenadas no representan distancias en las direcciones de los ejes del sistema:
Los sistemas más frecuentemente utilizados son el cartesiano o rectangular, el cilíndrico y el esférico.
 11.38.10.png)
1.8.1 Sistemas 2D
Un sistema en una dimensión es expresado por la recta numérica de los números reales y es estudiado en la educación primaria como una forma lineal de escala de referencia respecto al origen en el valor cero. En el caso de dos dimensiones, comúnmente se emplean dos tipos de sistemas de coordenadas: cartesiano (x-y) y el polar![]() . Un punto de interés específico en un sistema puede ser fácilmente expresada en el otro sistema a través de la trigonometría básica, como se muestra a continuación:
. Un punto de interés específico en un sistema puede ser fácilmente expresada en el otro sistema a través de la trigonometría básica, como se muestra a continuación:
|
|
Por ejemplo, podemos describir el punto P equivalente en ambos sistemas de coordenadas:
![]()
Tenga en cuenta que implícitamente se ha elegido un sistema de mano derecha de coordenadas, donde con x fluye hacia la derecha, punto y hacia arriba. Esto está en contraste con un sistema de la mano izquierda, en la que y se correría hacia abajo si x fluye a la derecha. Sistemas zurdos y diestros no se pueden intercambiar por una rotación pura (convénzase de esto). Pero requieren una inversión en conjunto con la rotación o un plano de simetría o espejo. Nosotros siempre elegiremos un sistema diestro.
Inspeccionar: http://demonstrations.wolfram.com/2DCoordinateSystemTransformations/
1.8.2 Sistemas 3D
En tres dimensiones, hay tres sistemas comunes de coordenadas que utilizaremos: los sistemas cartesiano (x,y,z) , cilíndrico ![]() y esférico
y esférico ![]() . Tenga en cuenta que el sistema cartesiano es todavía un diestro - si sus dedos apuntan a lo largo del eje x, y el pulgar a lo largo del eje y , el eje z señala el dorso de la mano para un sistema de mano derecha-. Tenga en cuenta que algunos autores utilizan diferentes convenciones para especificar ángulos y distancias, sobre todo en los sistemas cilíndrico y esférico.
. Tenga en cuenta que el sistema cartesiano es todavía un diestro - si sus dedos apuntan a lo largo del eje x, y el pulgar a lo largo del eje y , el eje z señala el dorso de la mano para un sistema de mano derecha-. Tenga en cuenta que algunos autores utilizan diferentes convenciones para especificar ángulos y distancias, sobre todo en los sistemas cilíndrico y esférico.
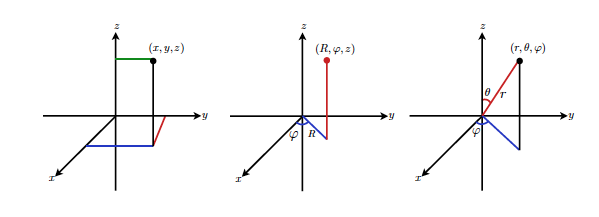
Sistemas de coordenadas en 3D: Izquierdo cartesiano(x,y,z) ; Centrado: cilíndrico![]() ; diestro o derecho esférico
; diestro o derecho esférico![]() .
.
Las interrelaciones entre estos tres sistemas de coordenadas también se derivan de la geometría básica, siempre y cuando uno se ocupe en las definiciones de los ángulos ![]() y de
y de ![]() . . . A continuación se lista el rango de las variables angulares dentro de las convenciones que vamos a adoptar, así como la interrelación entre los diferentes sistemas de coordenadas.
. . . A continuación se lista el rango de las variables angulares dentro de las convenciones que vamos a adoptar, así como la interrelación entre los diferentes sistemas de coordenadas.
 14.54.11.png)
Rango de variables angulares en sistemas de coordenadas en 3D
1.8.3 Sistemas de coordenadas de rotación en 2D
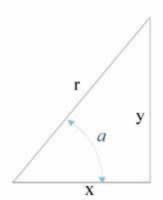
Primero un poco de trigonometría básica
|
donde tenemos las siguientes relaciones:
x = r cos a
y = r sen a
(hipotenusa)
algunas relaciones trigonométricas útiles:
Sen (a-b)= |
sen a cos b - cos a sen b |
Sen (a+b)= |
sen a cos b + cos a sen b |
Cos (a-b)= |
cos a cos b + sin a sen b |
Cos (a+b)= |
cos a cos b - sen a sen b |
En dos dimensiones. Tome un sistema normal (x, y), y seleccione un punto P (x, y). Un giro a la izquierda sobre el origen por el camino ( rotando x hacia y en un sistema de rotación con la mano derecha) significa que el punto P (x, y) se describe por las coordenadas P’ (x’, y’) en el marco rotado, como se muestra a continuación.
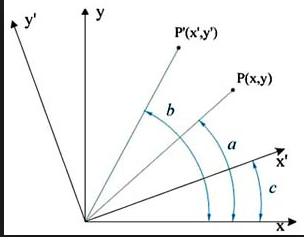
Rotación sobre un sistema de coordenadas 2D
Ver video tutor: https://www.youtube.com/watch?v=Da5cz-RN0Yw
Utilizando la trigonometría básica, podemos encontrar fácilmente una relación entre las dos representaciones de coordenadas:
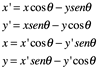
O podemos escribir esto en forma de matriz de ecuaciones.
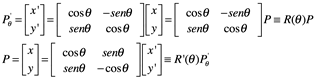
Aquí, la matriz ![]() actúa sobre el vector columna P, se conoce como una matriz de rotación, con bastante sensatez. Matrices de rotación deben tener un factor determinante de ± 1 en orden que preserve la longitud. Por otro lado, si hacemos una rotación en sentido horario sobre el origen
actúa sobre el vector columna P, se conoce como una matriz de rotación, con bastante sensatez. Matrices de rotación deben tener un factor determinante de ± 1 en orden que preserve la longitud. Por otro lado, si hacemos una rotación en sentido horario sobre el origen ![]() (rotación y hacia x en un sistema de mano derecha), las nuevas coordenadas después de la rotación son:
(rotación y hacia x en un sistema de mano derecha), las nuevas coordenadas después de la rotación son:
![]()
En términos de la matriz de rotación,
![]()
Tenga en cuenta que como se esperaba y son los sustitutos para y y viceversa. A continuación se presentan algunos ejemplos adicionales de rotaciones específicas en dos dimensiones:
|
Hacia la izquierda a 90º |
|
180º, I= matriz identidad |
|
Hacia la derecha a 90º |
Otro punto a destacar es que para una rotación alrededor de un origen fijo, las distancias del origen deben ser preservadas, el radio invariante. Esto requiere, en dos dimensiones:
![]()
que se pueda verificar que es verdad para las relaciones anteriores. Esto es equivalente a requerir que las matrices de rotación tienen un determinante de ± 1 (det R = ± 1), donde + y - se corresponde con rotaciones apropiadas e inapropiadas, respectivamente (véase más adelante). Esto también hace la matriz rotación sea afectada por transformaciones ortogonales.
Inspeccionar:
http://demonstrations.wolfram.com/2DRotationUsingMatrices/
http://demonstrations.wolfram.com/CoordinateTransformationOfAMatrixAndAlphaMatrix/
http://demonstrations.wolfram.com/RotationAboutAPointInThePlane/
1.8.4 Sistemas de coordenadas de rotación 3D
En tres dimensiones, tenemos tres tipos de rotaciones alrededor de un origen fijo a considerar: la rotación de las x, y, z hechas en sentido antihorario mientras observa el origen. Las tres matrices de rotación básicas (por un sistema de mano derecha de coordenadas) son:
|
Rota eje y hacia eje z |
|
Rota eje z hacia eje x |
|
Rota eje x hacia eje y |
Cualquier rotación se puede administrar como una composición de rotaciones alrededor de estos tres ejes, y por lo tanto, puede ser representado por una matriz de 3 x 3 que opera en un vector de columna que describe la posición.
1.9 Transformaciones de coordenadas
1.9.1 Sistema de coordenadas rectangular
Las superficies coordenadas son tres planos ortogonales entre sí:
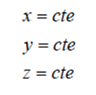
Un punto queda determinado por la intersección de estos tres planos y sus coordenadas vienen dadas por las tres constantes de los planos (x,y,z). Las líneas coordenadas son rectas perpendiculares entre sí y los vectores unitarios llevan sus direcciones, se denominan ![]() , por lo que un vector se escribirá:
, por lo que un vector se escribirá:
![]()
 19.50.49.png)
Como caso particular de este sistema de coordenadas, estos tres vectores se mantienen constantes en todos los puntos del espacio. También ocurre que las coordenadas son métricas, por lo que los factores de escala son la unidad y, en las direcciones de los ejes coordenados
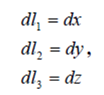
los diferenciales de longitud son los diferenciales de superficie en cada una de las superficies coordenadas.
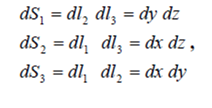
y el diferencial de volumen:
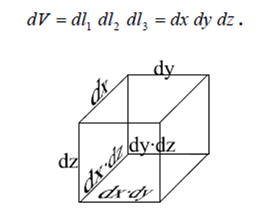
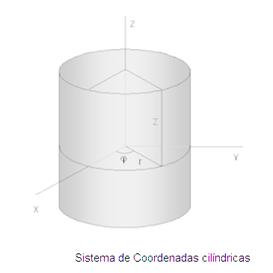
1.9.2 Sistema de coordenadas cilíndrico
Las superficies coordenadas son, planos Z = cte, semiplanos que contienen al eje z y forman un ángulo φ con el semiplano X-Z, y cilindros de eje z y radio ρ.
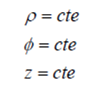
Las coordenadas de un punto vienen dadas por la intersección de tres de estas superficies, y se especifican mediante la terna (ρ,φ,z). Las líneas coordenadas ya no son todas rectas, y los vectores unitarios se denominan![]() . La dirección de los vectores
. La dirección de los vectores ![]() , varía según el punto del espacio considerado.
, varía según el punto del espacio considerado.
 19.53.17.png)
Las coordenadas ρ y z son métricas, por lo que el factor de escala es la unidad. Sin embargo la coordenada φ es angular, siendo el factor de escala ρ, de modo que un diferencial de arco en la coordenada φ mide dφ =ρ dφ:
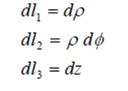
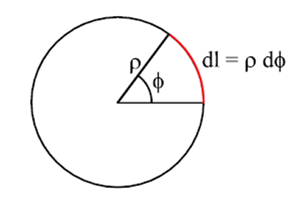
Los diferenciales de superficie, sobre las superficies coordenadas serán:
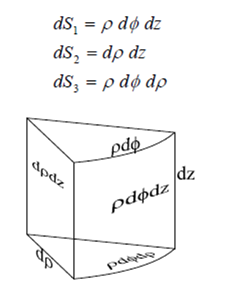
Por último, el diferencial de volumen es:
![]()
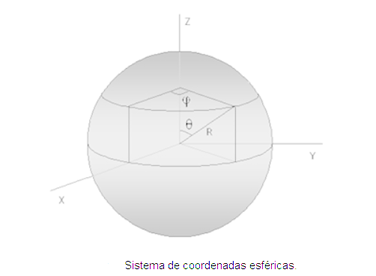
1.9.3 Sistema de coordenadas esférico
Las superficies coordenadas en el sistema de coordenadas esféricos son, una esfera de radio r, un cono de eje Z y centro el origen de coordenadas, cuya superficie forma un ángulo θ con el eje Z, y un semiplano que contiene al eje Z y forma un ángulo φ con el semiplano XZ.
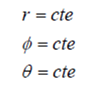
Las coordenadas de un punto vienen dadas por la terna (r,φ,θ), y los vectores unitarios ![]() . Todos los vectores varían su dirección según el punto del espacio considerado.
. Todos los vectores varían su dirección según el punto del espacio considerado.
 19.57.50.png)
Únicamente la coordenada r es métrica y le corresponde a un factor de escala 1. Para las coordenadas φ y θ los factores de escala son, respectivamente r sen(θ) y r:
 19.58.27.png)
Por lo que respecta a los diferenciales de superficie las expresiones son:
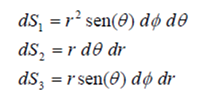
 19.59.19.png)
Por último un diferencial de volumen vendrá dado por:
 20.00.10.png)
1.9.4 Matrices de transformación de coordenadas
http://demonstrations.wolfram.com/CylindricalCoordinates/
http://demonstrations.wolfram.com/ExploringCylindricalCoordinates/
http://demonstrations.wolfram.com/SphericalCoordinates/
http://demonstrations.wolfram.com/ExploringSphericalCoordinates/
http://demonstrations.wolfram.com/SphericalCoordinateSystemWithUnitVectors/
Coordenadas polares
http://demonstrations.wolfram.com/PolarCoordinates/
Transformar coordenadas cartesianas a cilíndricas.
![]()
Transformar coordenadas cilíndricas a cartesianas
![]()

Conversión de coordenadas polares a rectangulares
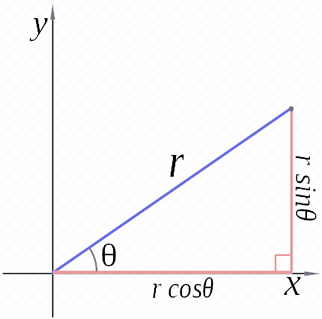
- Definido un punto en coordenadas polares por su ángulo θ sobre el eje x, y su distancia r al centro de coordenadas, se tiene:
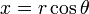
![]()
Conversión de coordenadas rectangulares a polares
- Definido un punto del plano por sus coordenadas rectangulares (x,y), se tiene que la coordenada polar r es:
![]() (aplicando el Teorema de Pitágoras)
(aplicando el Teorema de Pitágoras)
- Para determinar la coordenada angular θ, se deben distinguir dos casos:
- Para r = 0, el ángulo θ puede tomar cualquier valor real.
- Para r ≠ 0, para obtener un único valor de θ, debe limitarse a un intervalo de tamaño 2π. Por convención, los intervalos utilizados son [0, 2π) y (−π, π].
- Para obtener θ en el intervalo [0, 2π), se deben usar las siguientes fórmulas (arctan denota la inversa de la función tangente):
 20.02.38.png)
- Para obtener θ en el intervalo (−π, π], se deben usar las siguientes fórmulas:
 20.02.42.png)
http://demonstrations.wolfram.com/ConstantCoordinateCurvesForParabolicAndPolarCoordinates/
http://demonstrations.wolfram.com/PolarAreaSweep/
http://demonstrations.wolfram.com/SixSphereCoordinates/
- Normalización de vectores
- http://demonstrations.wolfram.com/3DVectorDecomposition/
- http://demonstrations.wolfram.com/EllipticCylindricalCoordinates/
- http://demonstrations.wolfram.com/ParabolicCylindricalCoordinates/
1.10 Operador DEL o Nabla
Desde geometría diferencial, nabla es un operador diferencial vectorial con símbolo ![]() y en coordenadas cartesianas está dado por:
y en coordenadas cartesianas está dado por:
![]()
o
![]()
en coordenadas cilíndricas
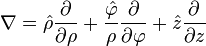
en coordenadas esféricas
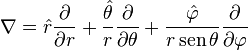
1.11 Gradiente y derivada direccional
El gradiente es la derivada vectorial, un campo de vectores dirección sobre las rectas tangentes a la curva f(x). Expresa dirección y velocidad de propagación.
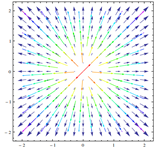
Supongamos que una cantidad escalar ![]() , tal como la humedad relativa del aire, se da como una función de cada punto para las regiones de un espacio
, tal como la humedad relativa del aire, se da como una función de cada punto para las regiones de un espacio ![]() . En un punto P, esta función tiene el valor
. En un punto P, esta función tiene el valor ![]() ; en otro punto P+dP, removiendo P por el diferencial de distancia dr, el valor de la función está dado por:
; en otro punto P+dP, removiendo P por el diferencial de distancia dr, el valor de la función está dado por:
![]()
![]()
![]()
![]()
Descartaremos los diferenciales de orden superior en el incremento de la función escalar entre los dos puntos P y P+ dP; se obtiene:
![]()
![]()
factorizar
![]()
Aquí ![]() es un vector unitario en la dirección del vector x, es decir, 1=
es un vector unitario en la dirección del vector x, es decir, 1=![]()
![]() ; similar para
; similar para ![]() y para
y para ![]() . El segundo paréntesis a la derecha en la última ecuación se trata de dr. El índice de soporte P, está implícito en las derivadas. Si el primer paréntesis se describe como
. El segundo paréntesis a la derecha en la última ecuación se trata de dr. El índice de soporte P, está implícito en las derivadas. Si el primer paréntesis se describe como ![]() (nabla phi o DEL phi), esta ecuación se transforma en:
(nabla phi o DEL phi), esta ecuación se transforma en:
![]()
![]() , es definido por la ecuación, es llamado gradiente de
, es definido por la ecuación, es llamado gradiente de ![]() y es aplicado en varios sistemas de coordenadas, además del cartesiano. A veces está escrito como grad o en notación simbólica
y es aplicado en varios sistemas de coordenadas, además del cartesiano. A veces está escrito como grad o en notación simbólica ![]() , que representa incremento de
, que representa incremento de ![]() , entre dos puntos separados por una distancia finita. Por tanto el valor del gradiente de phi es una derivada vectorial en coordenadas cartesianas:
, entre dos puntos separados por una distancia finita. Por tanto el valor del gradiente de phi es una derivada vectorial en coordenadas cartesianas:
![]()
en vectores unitarios
![]()
En cualquier sistema ![]() es una función vectorial obtenida por el producto de operador nabla por una función escalar. Considere que nabla no es una función, sino un operador vectorial, por sí mismo no tiene significado.
es una función vectorial obtenida por el producto de operador nabla por una función escalar. Considere que nabla no es una función, sino un operador vectorial, por sí mismo no tiene significado.
La magnitud de cambio ![]() , donde
, donde ![]() es el ángulo entre
es el ángulo entre ![]() y
y ![]() . Cuando dr es un vector que se encuentra a lo largo de la dirección de
. Cuando dr es un vector que se encuentra a lo largo de la dirección de![]() , el cambio resultante en
, el cambio resultante en ![]() tendrá su máximo valor en
tendrá su máximo valor en ![]() .
. ![]() por lo tanto, actúa como vector que apunta en la dirección de la máxima tasa de cambio de
por lo tanto, actúa como vector que apunta en la dirección de la máxima tasa de cambio de ![]() ; y el sentido del vector de la función vectorial
; y el sentido del vector de la función vectorial ![]() es tal que apunta a la dirección
es tal que apunta a la dirección ![]() creciente. La magnitud de este vectorial es
creciente. La magnitud de este vectorial es
![]()
El vector ![]() tiene la misma magnitud que
tiene la misma magnitud que![]() , solo que apunta en la dirección opuesta a la máxima tasa de incremento o propagación. Como ejemplo de un gradiente, nosotros podemos considerar una porción de una colina con altura sobre el nivel del mar h, en cualquier punto de la colina, es una función de posición h=h(x,y). Una versión simplificada del gradiente.
, solo que apunta en la dirección opuesta a la máxima tasa de incremento o propagación. Como ejemplo de un gradiente, nosotros podemos considerar una porción de una colina con altura sobre el nivel del mar h, en cualquier punto de la colina, es una función de posición h=h(x,y). Una versión simplificada del gradiente.
![]()
De la magnitud y dirección de la máxima tasa de cambio de altura en un momento dado, como lo ilustra la figura siguiente:
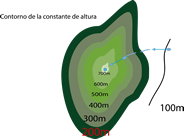
Este es un mapa topográfico bidimensional que utiliza la altura como parámetro. La magnitud de![]() , aquí es
, aquí es
![]()
La tasa de cambio de la altura con respecto a un desplazamiento horizontal. La dirección de ![]() es dada en la tasa de cambio de la máxima altura, a mayor altitud para un desplazamiento horizontal dr =dx+dy cuya dirección no es a lo largo de la dirección de
es dada en la tasa de cambio de la máxima altura, a mayor altitud para un desplazamiento horizontal dr =dx+dy cuya dirección no es a lo largo de la dirección de ![]() (aquí
(aquí ![]() está en el plano x-y) el cambio de la altura será
está en el plano x-y) el cambio de la altura será ![]() , donde
, donde ![]() es el ángulo entre el
es el ángulo entre el ![]() y el dr.
y el dr.
La derivada direccional de la altura, es una determinada dirección que se define como
![]()
y es igual a ![]() . Esto es inferior a la máxima tasa de cambio de altura, obtenida por el mismo dr, cuando dr está a lo largo de la dirección de
. Esto es inferior a la máxima tasa de cambio de altura, obtenida por el mismo dr, cuando dr está a lo largo de la dirección de![]() . Para
. Para ![]() la altura disminuye a una tasa máxima, el desplazamiento horizontal siendo opuesto en dirección a la del gradiente. La altura h en este análogo bidimensional del gradiente se distingue por no tener la dimensión z, del gradiente ordinario en 3D. La derivada direccional de una función es así la tasa de cambio de esa función en una dirección determinada. Si la derivada direccional es positiva en una dirección concreta, entonces la función está aumentando en esa dirección. El gradiente de una función en un punto es la derivada direccional en ese sentido para la tasa de cambio máxima.
la altura disminuye a una tasa máxima, el desplazamiento horizontal siendo opuesto en dirección a la del gradiente. La altura h en este análogo bidimensional del gradiente se distingue por no tener la dimensión z, del gradiente ordinario en 3D. La derivada direccional de una función es así la tasa de cambio de esa función en una dirección determinada. Si la derivada direccional es positiva en una dirección concreta, entonces la función está aumentando en esa dirección. El gradiente de una función en un punto es la derivada direccional en ese sentido para la tasa de cambio máxima.
Una función escalar cuya pendiente es cero en un punto es una función que tiene un máximo, mínimo o una inflexión allí. Si el gradiente es cero en todas partes, entonces la función escalar es una constante. Cuando el valor de esta constante es arbitrario es a menudo conveniente ponerlo igual a cero. Por ejemplo, podemos tomar ![]() sobre la superficie del océano. Entonces el nivel del mar puede tomarse como la medida de altura cero.
sobre la superficie del océano. Entonces el nivel del mar puede tomarse como la medida de altura cero.
Ejemplos 1:
Calcúlese el gradiente de la función escalar F
![]()
Solución:
![]()
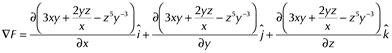
![]()
![]()
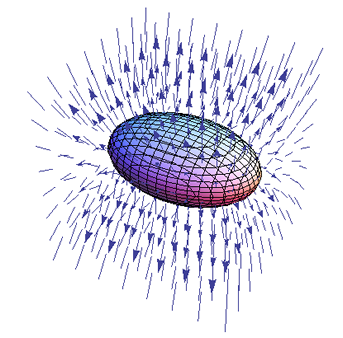

En Mathematica 10:
http://reference.wolfram.com/language/tutorial/VectorAnalysis.html
Software libre WinPlot para gráficar ecuaciones diferenciales
http://math.exeter.edu/rparris/winplot.html
Demostración
http://demonstrations.wolfram.com/VisualizingTheGradientVector/
http://demonstrations.wolfram.com/topic.html?topic=Multivariable+Calculus&limit=20
1.12 Divergente
Flujo. Una superficie cerrada es una superficie límite que divide un volumen en dos partes: un interior y un exterior. La superficie del mismo es limitada por una curva de superficie. Un área elemental de la superficie cerrada está representada por un diferencial vectorial de superficie dS que apunta al exterior, cuya área real de magnitud ![]() es ortogonal al vector dS que representa. La superficie de una seudo-esfera es una superficie cerrada, en ella en todos los puntos dS son radialmente hacia a fuera, de las dos direcciones posibles para dS, la convención universal es tomar la dirección que va de adentro hacia a fuera como positiva.
es ortogonal al vector dS que representa. La superficie de una seudo-esfera es una superficie cerrada, en ella en todos los puntos dS son radialmente hacia a fuera, de las dos direcciones posibles para dS, la convención universal es tomar la dirección que va de adentro hacia a fuera como positiva.

Una superficie abierta que está delimitada por una curva. La página de un libro es una superficie abierta y el borde de la página es la curva límite. Para una superficie dS abierta su magnitud es ![]() y dS es el vector perpendicular a la zona real representada. Aquí, además hay dos posibilidades para la dirección de dS, negativa y positiva; es decir, la positiva atravesó el perímetro de la lámina, negativa si las líneas de flujo ingresan a la lámina.
y dS es el vector perpendicular a la zona real representada. Aquí, además hay dos posibilidades para la dirección de dS, negativa y positiva; es decir, la positiva atravesó el perímetro de la lámina, negativa si las líneas de flujo ingresan a la lámina.
Es interesante señalar que no es posible dar definiciones rigurosas sin empleo de ejemplos mentales. El flujo de un campo vectorial ![]() se define por la superficie de entrada
se define por la superficie de entrada ![]() dada por
dada por
![]()
Se utiliza para simplificar la forma de integral cerrada, que en realidad cuando se integra es una integral doble, usando coordenadas variables. El flujo para este caso tiene dos valores, uno negativo y otro positivo dependiendo de donde se tome el vector normal u ortogonal. Para una superficie ![]() cerrada el flujo de un vector
cerrada el flujo de un vector ![]() únicamente es definido por
únicamente es definido por
![]()
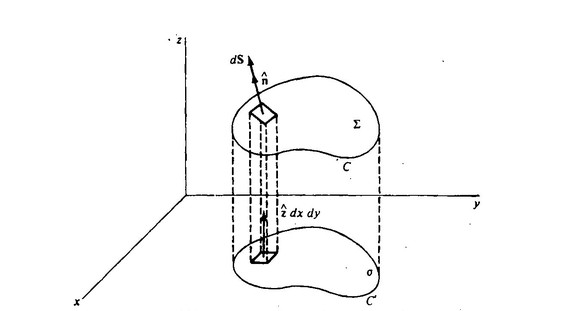
donde ![]() es un área abierta de una curva delimitada C, el área es proyectada en la superficie sobre el plano x-y. C’ es la proyección de C sobre el plano x-y. Donde es una superficie diferencial proyectada sobre el plano x-y. El pequeño círculo en la integral indica que la integración doble dxdy es una superficie cerrada y que la integración debe realizarse en toda la superficie. Para el flujo de un vector a través de una superficie curva, se puede usar el teorema que relaciona la integral de superficie proyectada
es un área abierta de una curva delimitada C, el área es proyectada en la superficie sobre el plano x-y. C’ es la proyección de C sobre el plano x-y. Donde es una superficie diferencial proyectada sobre el plano x-y. El pequeño círculo en la integral indica que la integración doble dxdy es una superficie cerrada y que la integración debe realizarse en toda la superficie. Para el flujo de un vector a través de una superficie curva, se puede usar el teorema que relaciona la integral de superficie proyectada ![]() y el ángulo entre
y el ángulo entre ![]() y
y ![]() ; y el coseno de este ángulo Cos (entre
; y el coseno de este ángulo Cos (entre ![]() y
y ![]() ) se relaciona con la superficie
) se relaciona con la superficie ![]()
![]()
Si la proyección es tomada sobre plano x-y, resulta que hubiera sido
![]()
Ahora vamos a definir la divergencia de la función vectorial ![]() en un punto P. Esto se da en términos de flujo hacia el exterior de
en un punto P. Esto se da en términos de flujo hacia el exterior de ![]() a través de una superficie cerrada
a través de una superficie cerrada ![]() , que contiene a P, y por el volumen v dentro. Si tenemos una superficie
, que contiene a P, y por el volumen v dentro. Si tenemos una superficie ![]() y un volumen
y un volumen ![]() . La razón forma el cociente
. La razón forma el cociente
![]()
Lo que da el flujo por volumen cerrado. Luego tomamos otra superficie ![]() que está enredando a
que está enredando a ![]() y al punto P. Forman una razón
y al punto P. Forman una razón ![]() en P
en P
![]()
Cuando este proceso sea continuo indefinidamente, entonces la relación acerca de un único límite se llama divergencia para cualquier sistema de coordenadas
![]()
La divergencia de ![]() es la fuerza de la fuente de flujo de
es la fuerza de la fuente de flujo de ![]() , definida en un punto. Ahora derivaremos una fórmula específica para la divergencia de
, definida en un punto. Ahora derivaremos una fórmula específica para la divergencia de ![]() cuando
cuando ![]() se da en el sistema de coordenadas cartesianas. Concederemos una caja pequeña finita rectangular cuyos bordes coinciden con los ejes x,y,z, que tiene en su centro el punto P(x,y,z,) como en la figura siguiente:
se da en el sistema de coordenadas cartesianas. Concederemos una caja pequeña finita rectangular cuyos bordes coinciden con los ejes x,y,z, que tiene en su centro el punto P(x,y,z,) como en la figura siguiente:
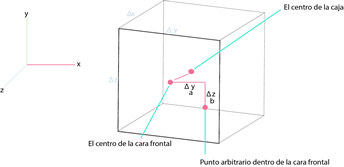
Eventualmente la caja será infinitesimal, con sus lados aproximados a cero. ![]() se convierte en la suma de seis integrales: sobre el frente, atrás, derecha, izquierda, arriba y abajo, respectivamente. Consideramos el frente de integración como la cara
se convierte en la suma de seis integrales: sobre el frente, atrás, derecha, izquierda, arriba y abajo, respectivamente. Consideramos el frente de integración como la cara ![]() . El valor de
. El valor de ![]() sobre la caja se obtiene a través de evaluar
sobre la caja se obtiene a través de evaluar ![]() ; en el centro de la caja por medio de una expansión de Taylor. El único componente de
; en el centro de la caja por medio de una expansión de Taylor. El único componente de ![]() que contribuye a la parte delantera es la componente x. Expresaremos esta componente como
que contribuye a la parte delantera es la componente x. Expresaremos esta componente como ![]() de
de ![]() evaluada en el centro P. La palabra caja pequeña aplica a una caja de lados aproximados a cero de primer orden de expansión:
evaluada en el centro P. La palabra caja pequeña aplica a una caja de lados aproximados a cero de primer orden de expansión:
![]()
Los factores a y b surgen de un punto en la cara frontal en una arbitraria posición: ![]() donde
donde ![]() .
.
Las derivadas, valuadas en P, son numéricas y pueden ser movidas a la izquierda del signo integral. Así los términos que involucra a y b cuando
![]()
Estos términos y condiciones de orden superior, contienen mayores potencias de los deltas. Por lo tanto, su distribución a la suma se convierte en extremadamente pequeña comparada con la de primer orden cuando ![]() y sin ser descuidados, como la caja es suficientemente pequeña, todos los puntos de la cara frontal pueden así ser considerados que están en el centro de la cara frontal. Puesto que
y sin ser descuidados, como la caja es suficientemente pequeña, todos los puntos de la cara frontal pueden así ser considerados que están en el centro de la cara frontal. Puesto que![]() es también un número, no una función, también se puede poner a la izquierda del signo de integración y se convierte la expresión en
es también un número, no una función, también se puede poner a la izquierda del signo de integración y se convierte la expresión en
![]()
Nosotros hacemos implícito en el paréntesis la evaluación en P.
En el caso de la segunda integral, se trata de la tapa trasera de la caja
![]()
también
![]()
Así se convierte en la segunda integral
![]()
Por consiguiente, la suma de las dos primera integrales, caras frontal y trasera de la caja, es
![]()
Por simetría, la tercera y cuarta integral dan
![]()
Asimismo, las siguientes dos últimas integrales
![]()
El flujo total de F por toda la superficie de la caja infinitesimal es
![]()
Si hacemos el volumen ![]() de la caja que tienda a cero
de la caja que tienda a cero
![]()
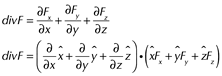
De manera explícita para div F en el sistema cartesiano es
![]()
Un vector cuya divergencia en todas partes es cero se llama vector solenoide. El nombre es referido al hecho de que en un campo magnético creado por un solenoide, la convergencia es cero.
Ejemplos 1:
Calcúlese el divergente de la función vectorial ![]()
![]()
Solución:
![]()
1.13 Rotor
El rotor de ![]() , en un punto P, ahora podemos definirlo considerando un vector cuya magnitud es el cociente de la circulación de
, en un punto P, ahora podemos definirlo considerando un vector cuya magnitud es el cociente de la circulación de ![]() a lo largo de un trazo C alrededor de un punto P, en un área delimitada por C. Asumimos que C se encuentra en un plano, así
a lo largo de un trazo C alrededor de un punto P, en un área delimitada por C. Asumimos que C se encuentra en un plano, así ![]() puede definirse; tomamos esta relación en el límite de
puede definirse; tomamos esta relación en el límite de ![]() y C reduciéndose a cero. Se asume que el límite de esa relación existe y es único.
y C reduciéndose a cero. Se asume que el límite de esa relación existe y es único.
La dirección del vector anterior es el de la normal a ![]() , el sentido positivo se relaciona en la forma de movimiento lineal de un tornillo de mano derecha relacionado con el movimiento de rotación. La magnitud y dirección de este vector dependerá de la ruta de C, lo cual es bastante arbitrario hasta aquí. Ahora asumimos que se sigue el mismo procedimiento para dar con un vector similar en este punto, pero en otra dirección. Luego que hagamos esto para todas las direcciones posibles, se asumirá que para algunas direcciones la magnitud del vector será máximo. El vector determinado por este procesamiento, en el sentido que maximiza la magnitud, se define como el rotor de
, el sentido positivo se relaciona en la forma de movimiento lineal de un tornillo de mano derecha relacionado con el movimiento de rotación. La magnitud y dirección de este vector dependerá de la ruta de C, lo cual es bastante arbitrario hasta aquí. Ahora asumimos que se sigue el mismo procedimiento para dar con un vector similar en este punto, pero en otra dirección. Luego que hagamos esto para todas las direcciones posibles, se asumirá que para algunas direcciones la magnitud del vector será máximo. El vector determinado por este procesamiento, en el sentido que maximiza la magnitud, se define como el rotor de ![]() en P. Las operaciones anteriores darán el componente de rotor de
en P. Las operaciones anteriores darán el componente de rotor de ![]() en la dirección normal a
en la dirección normal a![]() .
.
Si ![]() es un vector unitario en cualquier dirección particular y
es un vector unitario en cualquier dirección particular y ![]() es un camino cerrado en un plano perpendicular a
es un camino cerrado en un plano perpendicular a ![]() , entonces, para cualquier sistema de coordenadas, si
, entonces, para cualquier sistema de coordenadas, si ![]() es la zona delimitada por
es la zona delimitada por ![]() ,
,
![]()
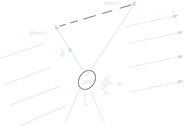
En la siguiente figura se muestra este procedimiento, que se supone que ![]() se hace infinitesimal. El resultado obtenido es el componente del rotor de
se hace infinitesimal. El resultado obtenido es el componente del rotor de ![]() , a lo largo de la dirección del vector unitario
, a lo largo de la dirección del vector unitario ![]() . Si
. Si ![]() es elegido en la dirección del rotor de
es elegido en la dirección del rotor de ![]() , en esta dirección es un máximo: el componente es igual a la magnitud del vector.
, en esta dirección es un máximo: el componente es igual a la magnitud del vector.
Nosotros ahora vamos a calcular una expresión para el rotor de ![]() , en coordenadas cartesianas.
, en coordenadas cartesianas.
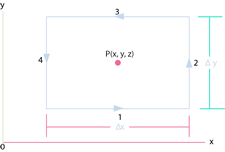
Considere el componente ![]() del rotor de
del rotor de ![]() :
:
![]()
Con los bordes ![]() y
y ![]() y el punto P(x,y,z) en el centro de la figura anterior. Entonces
y el punto P(x,y,z) en el centro de la figura anterior. Entonces ![]() y
y ![]() es
es ![]() . La circulación de
. La circulación de ![]() , es
, es ![]() y la integración de contorno puede dividirse en cuatro partes, todas ellas con z=constante:
y la integración de contorno puede dividirse en cuatro partes, todas ellas con z=constante:
1. De ![]() hasta
hasta ![]()
2. De ![]() hasta
hasta ![]()
3. De ![]() hasta
hasta ![]()
4. De ![]() hasta
hasta ![]()
Entonces ![]() , donde cada una de las cuatro integrales es
, donde cada una de las cuatro integrales es![]() .
.
Se obtienen los valores de los componentes de ![]() a lo largo de cuatro partes del camino de integración por expansión de Taylor. La pequeña área rectangular se convertirá posteriormente en un área diferencial, en la primera expresión se mantendrán los dos términos. Para la primera integral dy=0. Dejamos que
a lo largo de cuatro partes del camino de integración por expansión de Taylor. La pequeña área rectangular se convertirá posteriormente en un área diferencial, en la primera expresión se mantendrán los dos términos. Para la primera integral dy=0. Dejamos que ![]() represente la componente en x de
represente la componente en x de ![]() en P; entonces la componente en x de
en P; entonces la componente en x de ![]() en el primer segmento del contorno es
en el primer segmento del contorno es
![]()
donde a es un factor similar al utilizado en la derivada de la forma cartesiana en el divergente, cuya magnitud determina la posición de un punto a lo largo del primer tramo:![]() . El término que contiene a tendrá las contribuciones positivas y negativas que se cancelarán, dejando que el índice de la derivada sea implícito
. El término que contiene a tendrá las contribuciones positivas y negativas que se cancelarán, dejando que el índice de la derivada sea implícito
![]()
![]()
Para la segunda integral dx=0, entonces solamente el componente ![]() necesita ser evaluado:
necesita ser evaluado:
![]()
En términos de a da como antes cero; así que, con ![]() y sus derivadas evaluadas en P,
y sus derivadas evaluadas en P,
![]()
![]()
En caso de la tercera integral dy=0, otra vez, así que ![]() no necesitan ser considerados y la integral se convierte entonces
no necesitan ser considerados y la integral se convierte entonces
![]()
![]()
Tenga en cuenta que la expresión para la diferencial aquí es +dx, solo en cuanto a la primera integral; pero los límites se invierten. También sería correcto mantener los límites igual que antes si, en lugar de usar +dx, fuera empleado –dx. Pero sería incorrecto invertir tanto los límites y el signo de la variable independiente. Así que
![]()
Asimismo, para el cuarto camino dx=0y la integral se convierte en
![]()
![]()
Sumando las cuatro contribuciones
![]()
Por lo tanto
![]()
Por tanto de manera similar las componentes x ,y, z del rotor F pueden obtenerse por la permutación cíclica de x, y y z. Dejando que
![]()
Dando
![]()
otra permutación cíclica de x,y, z nos da
![]()
En coordenadas cartesianas la expresión del rotor de F, por tanto es
![]()
Usando las reglas para la expresión de un determinante, este resultado se puede expresar
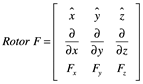
![]()
Donde el operador en coordenadas cartesianas tiene el mismo valor que tiene para el gradiente y el divergente.
Cuando se utiliza el símbolo de rotor el operador transforma un campo vectorial. En el caso de la pendiente en un punto dado, hay una tasa máxima de cambio de rotación para una función escalar en alguna dirección; a lo largo de cualquier otra dirección la tasa de cambio de la función escalar es igual a la tasa máxima de cambio multiplicada por el coseno del ángulo entre las dos direcciones. La tasa máxima de cambio y dirección particular especifican el vector gradiente. Asimismo, en el caso de los rotores en un punto dado, hay una circulación máxima de la función vectorial por unidad de área cerrada infinitesimal en alguna dirección; a lo largo de cualquier otra dirección la circulación por unidad de superficie es igual al valor máximo multiplicado por el coseno del ángulo entre las dos direcciones.
Un rotor cuyo vector en todas partes es cero, se denomina irrotacional o laminar. El nombre significa que no hay ninguna rotación; es decir, no hay circulación.
1.14 Laplaciano
Supongamos que uno toma la divergencia de una función vectorial, en términos del gradiente de una función escalar en coordenadas cartesianas:
![]()
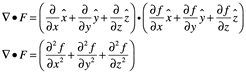
Esto se define como el Laplaciano de F. y se expresa como ![]() .Significa el divergente del gradiente de F. En física el Laplaciano se refiere a un operador elíptico de segundo orden que expresa la teoría del potencial, la propagación de ondas, la conducción de calor, la distribución de tensiones en un sólido deformable.
.Significa el divergente del gradiente de F. En física el Laplaciano se refiere a un operador elíptico de segundo orden que expresa la teoría del potencial, la propagación de ondas, la conducción de calor, la distribución de tensiones en un sólido deformable.
URL sugerida
http://www.revistaciencias.com/publicaciones/EpyuVkpVAAKxbHWgMt.php
[1] Sánchez, M. J. Manuel (2011), Historia de Matemáticas Hamilton y el descubrimiento de los cuaterniones. Pensamiento matemático. Recuperado de
http://www2.caminos.upm.es/Departamentos/matematicas/revistapm/revista_impresa/numero_1/hamilton_y_el_descubrimiento_de_los_cuaterniones.pdf
[2] http://revistasuma.es/IMG/pdf/25/061-070.pdf
[3] A History of Vector Analysis: The Evolution of the Idea of a Vectorial System (Notre Dame, Indiana: University of Notre Dame Press, 1967), xviii + 270 pp;(New York: Dover, 1985; 1994)