Texto académico

Autores

Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Gladys Juárez Cisneros
Filho Enrique Borjas García
Lizbeth Guadalupe Villalon Magallan
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán

5. Matemática elemental

En el libro intitulado “pensamiento matemático^[1]”, en él se discutieron las diferentes matemáticas que se consideran en el siglo XXI como elementales. Son enseñadas en la primaria, secundaria y bachillerato de la mayor parte del mundo, aunque no todas estas en cada grado escolar. Sin embargo, esto plantea la pregunta de ¿hasta dónde está la frontera de las matemáticas elementales? Por desgracia no está claro el límite entre la matemática elemental y la universitaria (avanzada). Las elementales más obvias las discutiremos en esta obra. Sin duda que en este espacio de pensamiento están objetos matemáticos y conceptos como el infinito, la abstracción, la demostración, geometría, álgebra arábiga, topología, cero, pi, número, operadores…

Algunos matemáticos consideran a las temáticas de matemáticas elementales al número, aritmética, geometría, álgebra, cálculo y algunos temas de probabilidad y estadística. Sin embargo, en muchos países desarrollados, para sus sociedades consideran además la matemática computacional y el álgebra lineal. Está claro que la matemática computacional tiene que ver en como la sociedad de hoy organiza sus comunicaciones, economía, educación y cultura; mientras el álgebra lineal por su enorme potencial para modelar lo complejo en forma relativamente más simple.  

El problema de los numerales

La computación siempre ha sido parte de la técnica de las matemáticas, pero no se convierte en un concepto matemático elemental hasta el siglo XX. La definición más conocida de este concepto, la realizó en 1936 Turing, en función de los cálculos de cómputo utilizados en la aritmética elemental. Llevar a cabo los cómputos de la aritmética estimula al aprendiz a sistematizar pasos algorítmicos necesarios para emplear o aplicar la tecnología programable de nuestro tiempo.

Sí un problema puede ser resuelto por un ordenador y si el cómputo es factible para acelerar el aprendizaje del pensamiento matemático, se vuelve este tema más que relevante para el aprendizaje de las nuevas generaciones, en este mismo sentido  Conrad Wolfram opina:  

“Conrad Wolfram (Oxford, 1970) piensa que tenemos un problema con las matemáticas. Nadie está contento: los estudiantes creen que es una asignatura difícil y sin interés, los maestros están frustrados con los resultados de sus alumnos y los gobiernos se dan cuenta de que son determinantes para la economía pero no saben cómo actualizar los programas académicos. Cada vez vivimos en un mundo más matemático y sin embargo, la educación está estancada, opina Wolfram, físico y matemático por la Universidad de Cambridge y fundador de Computer Based Math, una compañía centrada en rediseñar la asignatura de matemáticas”…”Respuesta. Los matemáticos me odiarán por decir esto, pero antes de los ordenadores las matemáticas no eran muy útiles para el día a día, en la vida en general. Para cualquier campo en el que se usen muchos datos, como la física, la biología o la salud, la computación ha elevado las matemáticas a un estadio nuevo. Los problemas reales del siglo XXI solo se pueden resolver usando los ordenadores y por eso deben entrar en el sistema educativo como parte fundamental de la asignatura de matemáticas. Tener a los niños en las aulas calculando a mano ecuaciones de segundo grado ya no tiene sentido; hay que enseñarles a interpretar los datos y a sacar utilidad de las matemáticas. Enseñarles el funcionamiento básico está bien, pero complicarlo hasta la extenuación es una estrategia errónea que les aleja para toda la vida. Suelo poner el ejemplo de la conducción; no hace falta entender el funcionamiento de los motores para manejar un vehículo^[2]”.

Agregar a la clase de matemáticas de las nuevas generaciones, procedimientos sistemáticos que toman gran cantidad de tiempo, intensifica la frustración en el caso de verificar soluciones y rápidamente descomponer en factores algebraicos una gran cantidad de procedimientos de problemas matemáticos. Sin embargo, el rol del pensamiento matemático se vuelve relevante cuando se asiste por ordenador el aprendizaje de las matemáticas, por favor, invierta un tiempo a conocer por ejemplo, el Wolfram Alpha (https://www.wolframalpha.com), poderosa herramienta de conocimiento computacional matemático. 

Muchos datos interesantes de los números, se discuten en la sección “¿qué es un número”,  sin embargo, demostrar que son infinitos los números primos por ejemplo, no depende de los números decimales. Pero cuando se trata de cómputo incluso operaciones simples tales como la adición y la multiplicación, la notación para números para ingeniería y ciencia, o cambios de base numérica con exponenciales; este cambio hace necesario el conocimiento informático. 

En base 1, un número es representado por n copias del dígito 1. Así el numeral en base 1  con longitud n dígitos, en esta notación simple de la aritmética, se vuelve  geometría más que aritmética. Por ejemplo, decimos que si m es menor que n, está claro que es el caso:

5<9 en notación base 10.

La suma es igual de fácil:

Es trivial observar que la base 1, no es práctica para tratar con números grandes. Multiplicar n por m, aumenta la longitud del número resultante, por lo que uno rápidamente se queda sin espacio para escribir el resultado de multiplicaciones repetidas. Necesitamos una notación más compacta y esto lo logramos mediante el uso de dos o más dígitos. 

Un numeral de base 10 como todos sabemos, es una cadena de dígitos elegidos entre el conjunto 0,1,2,3,4,5,6,7,8,9 y con un dígito más a la izquierda diferente de cero podemos extender la capacidad de contar hasta cadenas de números que podemos representar con n dígitos, cada uno de ellos representando un número diferente. Para las cadenas comenzamos con cero a la izquierda, solo que ignoramos por economía estos ceros en la primera cadena de un solo dígito. Así, la notación base 10 es más compacta con 10 símbolos, si además la expresamos en forma exponencial, la longitud se presenta en forma más compacta para números grandes. Pero hay un precio a pagar con notación compacta. En comparación con las sumas y multiplicaciones simples de la notación base 1, algunas operaciones son apenas factibles para nosotros sin asistencia de un ordenador. Si deseamos encontrar qué número es más pequeño para el caso siguiente, tenemos que buscar para el dígito más a la izquierda dónde se diferencian, y el número más pequeño es el que en la cifra es menor:

Esta regla para ordenar numerales es llamada orden lexicográfico, ya que es como la regla para ordenar palabras de la misma longitud en un diccionario. Igual que uno necesita saber del orden alfabético para buscar palabras en las entradas de diccionario, lo que debemos saber es el orden de dígitos con el fin de comparar su peso de cada número en base 10.  

El más simple alfabeto para escribir números compactos es el alfabeto binario o de base 2. Que consiste en dos símbolos, 0 y 1. Base 2 es digna de su estudio, no solo porque toda tecnología digital depende de ello, sino por su simpleza y compactación que nos ayuda a tomar conciencia del funcionamiento de la base 10, que la mayoría de nosotros ha olvidado por la lejanía de los estudios de educación primaria. 

Un número de base 2, es decir, 101001 representa un número como la suma de las ponencias de los pesos de cada posición del numeral dígito, por ejemplo: donde los pesos son para cada posición.

Así que el número binario 101001 es en base 10 el 41.

Caso contrario, para pasar de base 10 a binaria un número, por ejemplo: 7901

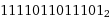
Podemos ver que para saber el numeral binario requerimos operaciones de multiplicación y exponenciación. Por lo tanto, necesitamos un conjunto más sofisticado de conceptos para encontrar “nombres” más convenientes para los números. No es de extrañar que la aritmética de números sea un tema profundo. De hecho, algunas de las preguntas más difíciles en teoría de números implican la representación decimal o binaria, por ejemplo, ¿Cuántos números primos hay cuyos dígitos binarios todos sean 1? No sabemos si esto es como intentar saber si hay infinitos números primos de la forma 2n + 1.

El problema de la adición de grandes números

Para comprender lo que sucede con la base 10 cuando añadimos números a cifras, considere por ejemplo, 7924 + 6803. Si ampliamos los números como sumas de potencias de 10 y los escribimos en coeficientes, entonces:

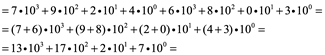
La última línea no se traduce inmediatamente en una base 10, porque los coeficientes no son menores a 10. Aquellos mayores de 10, como 13=10+3, crean un desbordamiento de potencias mayores de 10, que deben ser acarreados a la izquierda y agregados a los coeficientes ya presentes. En este caso, obtenemos una potencia extra a la de , es decir, . Porque: 

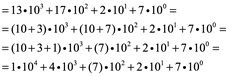
= 14,727

El acarreo de números comenzó con el  ábaco chino. Este método permite emplear máquinas para procesar este tipo de operaciones. Esto es muy deseable para cuando el tiempo y la eficiencia computacional requerida es más corto que el que al cerebro humano le toma en hacerlo. 

El problema de la multiplicación de grandes números

La dificultad de la multiplicación, por un lado, es el no verla como resultado de una matriz de dos dimensiones cuyos cuadrados son de tamaño unidad, y por otro, el análisis de multiplicar números grandes. El primer caso escapa al nivel de este texto, pero se enseña a nivel de educación primaria. El segundo plantea problemas como el de multiplicar los números 44227 y 935. Que hace implícito trabajar los dígitos individuales de 935 por 44227. 

Tradicionalmente:

44227x9=398043

44227x3=132681

44227x5=221135

De esto concluimos que por la posición del numeral: 

4227x900=39804300

4227x30  =1326810

4227x5.   =221135

De la que obtenemos 4227x935 mediante la suma de los tres numerales: 

El número de dígitos en la tabla es una medida de la razonable dificultad y tiempo necesario para el cómputo, ya que el tiempo razonable se obtiene para cada dígito como una constante. Las constantes reflejan la cantidad máxima de aritmética mental necesaria para cada dígito que multiplicamos y el número de sumas para el resultado final. 

Muchos lectores no saben lo que es un teorema y que es fácil de solucionar: un teorema es una declaración matemática verdadera, a menudo uno  que expresa algo verdadero sobre  cada caso de cierto tipo. Por ejemplo:

Teorema: Un número es divisible por 9, sí y solo sí la suma de sus dígitos es divisible por 9. 

Por ahora no examinaremos el teorema, solo pretendemos que no sea aquí un concepto esotérico que nadie entiende. Algunos teoremas son fáciles de comprender y otros son difíciles de ver su verdad que expresan. El de Pitágoras es de los sencillos y el de Fermat de los difíciles. Para la multiplicación, es relevante  la relación bidimensional de una matriz que proporciona la idea de cómo funciona. El trabajo de memoria con ayuda de la matriz  es más reducido para el cálculo y ver a la multiplicación como unidades derivadas de un cuadrado LxL, con L=1.  

Así, el pensamiento matemático no es memorizar información fáctica, es preferible reconstruirlo usando las relaciones generales o teoremas. La matriz puede tratarse como genérica en el sentido que 3 y 7, tendrán una misma propiedad que otros pares de números. 

La división

Cuando a y b son enteros positivos, a no es usualmente divisible por b, así que la operación de la división en general expresa un resto. Es decir, para a y b deseamos encontrar el cociente y el resto tal que:

Con

Si dividimos 34781 entre 26. La idea es analizar las cifras de 34781  de izquierda a derecha, en cada paso de división por 26 a su vez. Cada coeficiente es un número dígito, por lo que no es realmente necesario saber dividir por 26 -solo ahora multiplicar 26 por cada número de una cifra . Aquí están los cinco pasos en el cálculo de este ejemplo:

Divide 3 por 26 obtiene cociente 0 y resto 3,

Entonces divide 34 por 26 obtiene cociente 1 y resto 8,

Entonces divide 87 por 26 obtiene cociente 3 y resto 9,

Entonces divide 98 por 26 obtiene cociente 3 y resto 20;

Entonces divide 201 por 26 obtiene cociente 7 y resto 19.

El cociente de 34781 por 26 es entonces la secuencia de cifras del cociente, 1337 y el resto es 19. Uno puede ver cómo funciona la interpretación de las cifras 34781, como número de unidades, decenas, centenas  y así sucesivamente. Por ejemplo, 34  supera los miles, por lo que el cociente de 26 es 1 mil con resto 8 mil. Colocar este resto a la cifra siguiente, 7, que significa cientos, 87 cientos. Así que su cociente de 26 es 3 cientos con 9 cientos de resto y así sucesivamente. 

En general, si utilizamos el método de dividir un número a de m dígitos por un número b de n dígitos hay m pasos necesarios, cada uno de los cuales, el número de dígitos del número b multiplicado por un dígito y restado de un número obtenido previamente con el fin de obtener un resto <b. Puesto que solo hay 10 dígitos posibles a ser juzgados, el tiempo de cada m paso está delimitado por un múltiplo constante de mn, como se afirma.

Exponenciación

El caso más sencillo es elevar 10 a la potencia N, da un 1 seguido de N ceros. Por ejemplo, la base numeral 10 para es un 1 seguido de un millón de ceros. Así, solo se escribe el numeral 11 base  para como exponencial de los números M y N. La situación es similar con números de base 2. Así, el hecho de que números de base 10 pueden representar completamente a números muy grandes tiene un inconveniente, la exponenciación de números muy cortos  resulta en números muy largos. Así que no es factible la exponenciación para calcular la adición y la multiplicación. Independiente de cómo computamos , el tiempo para escribir el resultado generalmente impide completar el cómputo. 

Máquinas de Turing

Como hemos visto, se han utilizado varios tipos de computación aritmética durante miles de años. Sin embargo, la necesidad de un concepto general de cálculo no se consideró hasta principios del siglo XX.  Se presentó de otra forma de cómputo: lógica simbólica. La idea de lógica simbólica, era el sueño de Leibniz en el siglo XVII, consiste en hacer del razonamiento una forma de cálculo. Entonces, para resolver un problema simplemente diríamos “vamos a calcular”. Como él idealizo, el sueño no se realizó aún parcialmente hasta el siglo XIX, y sigue siendo un problema hoy en día, por razones tales como el misterio de P y NP. Sin embargo, encontramos el significado de la lógica simbólica y su cálculo. 

Un problema P se dice que tiene solución en el tiempo de cálculo,  es en relación al número de símbolos que contiene. Cuando un problema cuyas respuestas son difíciles de encontrar, sin embargo, fáciles de verificar, están por todas partes, su tiempo es no determinista (NP).

El punto principal a entender es como reducir todas las formas concebidas de razonamiento al cálculo. Los primeros en captar este punto, tuvieron aparición en 1921. Propusieron una definición de computación: generalización de los sistemas de lógica simbólica. Sin embargo, Turing llegó a su concepto de máquina mediante el análisis de cómo lo calcula un ser humano. Como mínimo, el cómputo humano requiere una cantidad limitada de entradas mentales para guiar el lápiz, y un papel. El papel fue una cinta dividida en cuadritos, cada uno de los cuales puede llevar un solo símbolo. El lápiz también llamado cabeza lectura/escritura, es un dispositivo que puede reconocer y escribir un número finito de símbolos , donde denotan el vacío gráfico.  Por último, la máquina tiene un número finito de estados internos que corresponden a los estados mentales necesarios para el cómputo dado. Como hemos visto, los cómputos pueden realizarse utilizando solo un número finito de estados mentales y Turing sostuvo que ningún cálculo podría requerir infinitamente muchos estados mentales, algunos de ellos serían tan similares que serían confundidos. Por lo mismo, un cálculo no implica infinitamente muchos símbolos diferentes. 

...una ilimitada capacidad de memoria obtenida en la forma de una cinta infinita marcada con cuadrados, en cada uno de los cuales podría imprimirse un símbolo. En cualquier momento hay un símbolo en la máquina; llamado el símbolo leído. La máquina puede alterar el símbolo leído y su comportamiento está en parte determinado por ese símbolo, pero los símbolos en otros lugares de la cinta no afectan el comportamiento de la máquina. Sin embargo, la cinta se puede mover hacia adelante y hacia atrás a través de la máquina, siendo esto una de las operaciones elementales de la máquina. Por lo tanto, cualquier símbolo en la cinta puede tener finalmente una oportunidad^[3].

Por esta razón, una máquina de Turing tiene finitos y . ¿Cómo funciona la máquina? Realiza una serie de pasos, en cada paso la cabeza de lectura/ escritura se observa el símbolo actualmente a la vista y dependiendo de su estado interno actual, sustituye a por un símbolo , por lo que, se mueve un cuadro a la izquierda o la derecha y entra en un estado . Así, una máquina M es especificada por una tabla de quíntuples, instando la acción a ser realizada por determinados pares de , . 

Ejemplo^[4]: 

Diseñar una máquina de Turing para realizar un determinado cálculo, aunque tedioso, es básicamente una cuestión de pensamiento de cómo hacer si se ve solamente un símbolo a la vez. Con algo de práctica, uno se convence de que cualquier cálculo es posible, por lo que, es intuitivamente plausible que máquinas de Turing puedan calcular cualquier cosa que sea computable. Se ha comprobado que todos los modelos propuestos de cómputo pueden ser simulados por maquinas Turing.

La Tesis de Church-Turing establece que cualquier función que sea procesada por un cierto algoritmo es una función computable; son exactamente las funciones que pueden ser calculadas con una máquina. Algoritmo, muchos autores, lo refieren como listas de instrucciones para resolver un cálculo o un problema abstracto, es decir, son un número finito de pasos que convierten los datos de un problema (entrada) en una solución (salida^[5]). Todo algoritmo es equivalente a una máquina de Turing. 

Definiendo el concepto de máquina informática, se reconoce la existencia de un algoritmo, como un P problema solucionable. Así, una máquina de Turing es esencialmente un programa, escrito en un lenguaje de programación. Esto es claro en la formulación de Post en 1936, que mejora la comprensión, al llamar  números de instrucciones al conjunto, en vez de estados internos como lo refirió Turing. 

El descubrimiento de la notación compacta para los números y los métodos para calcular sus sumas y productos, se remontan a miles de años. En Europa y el lejano Oriente fueron inicialmente implementados en el ábaco. El cálculo escrito se convirtió en práctica después de la invención de un símbolo para el cero en la India alrededor siglo quinto A.C., notación posicional para extender los números que fue adoptada por el mundo árabe (números arábigos)  y luego en Europa con los moros en España. Pero fue con los Mayas y su indeterminación de cantidad  que se define al cero como número y no solo como auxiliar en un sistema numérico. Así, el cómputo fue sinónimo de ábaco. Pero realmente el cálculo simbólico avanzó con el álgebra del siglo XVI. Newton, Euler y Gauss dieron forma al cálculo numérico y simbólico. Tan pronto como Leibniz previó la posibilidad de un razonador de cálculo, un lenguaje simbólico para el razonamiento se hizo una tarea en el horizonte del cómputo. El primer paso concreto hacia este sueño fue realizado por Boole en 1847, que creó un simbolismo algebraico por lo que ahora llamamos lógica proposicional. Boole manejó suma (+), multiplicación (·) y los operadores “o”, y “y”, 0 y 1 para falso y verdadero. Entonces su suma (+) y multiplicación (·) satisficieron leyes similares a las de la aritmética ordinaria, y uno puede decir si ciertos tipos de declaraciones son verdaderas por cálculo algebraico. De hecho, si p+q se toma para significar “ p o q pero no ambos”, entonces las reglas algebraicas de la lógica proposicional se convierten exactamente en las del mod 2 aritmético. La lógica proposicional de Boole reduce la lógica básica del cálculo inspirado por Frege en 1870, Peano 1895 y Russell 1910 para desarrollar sistemas simbólicos completos para las matemáticas. El objetivo de estos sistemas formales, era evitar errores inconscientes por sesgos cognitivos. Se pueden seguir los pasos de una prueba formal sin saber el significado de los símbolos por lo que, en principio, una prueba formal puede comprobarse por una máquina. De hecho, las demostraciones formales pueden en principio ser generadas por una máquina, mediante la combinación que generan todas las posibles cadenas de símbolos con que se prueba sin una cadena dada es valida.  

En el momento cuando se desarrollan los primeros sistemas formales, tales máquinas no habían sido construidas, así la compatibilidad fue imaginada como un concepto matemático.  Pero la idea despertó poco a poco que los sistemas formales incluyendo todos los procesos de cómputo posibles, podrían ser manipulados como símbolos más generales concebibles en sistemas formales que lograron simplificar la lógica al punto mecánico de establecer verdad o falsedad como Leibniz  había imaginado. Cualquier problema inservible NP, implica una cantidad infinita de incompletitud.  Gödel fue capaz de demostrar la incompletitud de los sistemas formales en matemáticas, es decir, cualquier sistema en su aritmetización del cálculo simbólico o lógico, puede ser simulado por números, en última instancia, definibles en términos de operaciones suma (+) y multiplicación (·), en cierto sentido todos los cálculos son ábacos o cómputos suma (+) y multiplicación (·) inherentes a la solución.

En resumen, el cómputo es ahora uno de los conceptos fundamentales de las matemáticas. El concepto de máquina de Turing es el modelo más sencillo y más convincente de la informática. El concepto es muy simple, no es mucho más complicado que los algoritmos para la suma  y la multiplicación de números decimales. A pesar de su sencillez, solo hasta hace 15 años aproximadamente los países desarrollados introdujeron este conocimiento en los niños de entre 8 y 13 años, como base de su formación aritmética y soporte para desarrollar el edificio mental de la lógica matemática y ampliar su rol conceptual con la computación moderna presente en telefónica celular, autos y ordenadores de todo propósito.

Durante miles de años los matemáticos han hecho cálculos, así que siempre ha habido un concepto de computación aunque algo vago en sus inicios. Esto comenzó con la formalización de Euclides del concepto de “geometría” en “Elements”, y la recolección de pasos alrededor de 1900 cuando Peano (1889) formalizó la aritmética con axiomas para los números naturales y Zermelo (1908) formalizó la teoría de conjuntos con una base axiomática para ellos. Pero esta formalización recibió un duro revés por Gödel (1931), demostrando que todo sistema de axiomas de la teoría de números y de conjuntos es incompleto, probando que la formalización de la aritmética no es posible, después de todo Gödel creía que su argumento mostraría que el concepto de compatibilidad no puede ser formalizado. Era incorrecto verlo como máquina de Turing. Pero más tarde reconoció su error en un libro de 1946, dijo “es una especie de milagro”, sí es posible formalizar la computabilidad. Así, computabilidad es realmente un concepto más preciso y absoluto que el concepto de la aritmética. Esto es un descubrimiento que abre la puerta a crear la inteligencia artificial.

Referencias

[1] http://www.libertadacademica.com/EbookLetras3/elements/TablaContenido.html

[2] El País (2017) Conrad Wolfram, físico que está cambiando la forma de enseñar matemáticas en Estonia, apuesta por eliminar el cálculo a mano.

[3] Bernhardt, C. (2017). Turing’s Vision: The Birth of Computer Science (The MIT Press) (Reprint ed.). The MIT Press.

[4] https://es.wikipedia.org/wiki/Máquina_de_Turing#cite_note-2

[5] Brassard, Gilles; Bratley, Paul (1997). Fundamentos de Algoritmia. Madrid: PRENTICE HALL.