Texto académico
Autores
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Gladys Juárez Cisneros
Filho Enrique Borjas García
Lizbeth Guadalupe Villalon Magallan
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán

Introducción
El número
El lenguaje nos permite etiquetar infinitamente muchos números diferentes. Estas etiquetas, las más evolucionadas, son los números arábigos, estos pueden simbolizar y discretizar cualquier cantidad continua. Gracias a ellos, podemos distinguir los números como aproximados a una cantidad, pero cuyas propiedades aritméticas son algo diferente de solo contar uno a uno. Solo entonces se puede concebir la invención de las reglas puramente formales para comparar, agregar o dividir dos números. Así, los números adquieren una idea carente de cualquier exigencia directa a un conjunto de objetos materiales. El andamiaje de las matemáticas entonces puede elevarse, cada vez más alto, cada vez más abstracto.
La cultura evoluciona mucho más rápido que nuestra genética. Esto ocurre así, dado por un proceso de invención de ideas. El concepto de número, si bien surge de la base biológica que nos permite reconocer patrones de cantidades, claro está, la unidad incluida; este concepto fue insinuado por babilonios, griegos, indios, egipcios, mayas…, hasta su purificación y refinamiento cultural. Galois, Bedekind y Peano, ellos resolvieron su axiomatizado empujando la cultura a la matemática moderna. Ahora nuestro cerebro se enfrenta a una tarea fascinante de abstracción matemática, para la cual la evolución biológica no nos preparó; como resolver ecuaciones, multiplicar fraccionarios, resolver funciones, factorizaciones. A partir del acumulador de aproximación con que contamos el tiempo, compartido por otras especies como ratones y palomas, nuestro cerebro que no contiene innato ninguna cantidad aritmética destinada para la idea de número. Compensa esta deficiencia, jugando con circuitos alternativos en nuestra red cerebral. Palabras y números son educados hasta lograr que sean tan intrusivos que reemplazan completamente la función de áreas cerebrales. La alfabetización nos entrena a reconocer las letras y los números insinuándolos como objetos visuales y asociándolos con un sistema de interpretación.
Algunos objetos matemáticos ahora parecen muy intuitivos solo porque su estructura está bien adaptada a nuestra arquitectura cerebral. Por otro lado, muchos jóvenes tienen problemas para realizar una suma de fraccionarios, porque su maquinaria cortical resiste a modificarse con el concepto contraintuitivo. Si la biología del cerebro muestra resistencia a imponer límites a nuestra comprensión aritmética, ¿cómo prosperar en el pensamiento matemático? No existe evidencia de que las grandes mentes matemáticas de la historia, hayan sido dotados de una estructura neurobiológica excepcional. Al igual que el resto de nosotros, los genios en aritmética tienen que luchar con cálculos y conceptos matemáticos. Si tienen éxito, es solo porque dedican un tiempo considerable a este tema y finalmente inventan algoritmos bien ajustados y atajos inteligentes para aprovechar sus propiedades en la solución de problemas y definiciones. Lo especial en ellos es su pasión, la seriedad con que se toman su trabajo y la confianza depositada tanto en la literatura como en el profesor, además, del apoyo de sus padres, docentes y compañeros en el desarrollo responsable cultura matemática.
Álgebra
Para aprovechar el poder del álgebra, necesitamos un sistema numérico que satisfaga sus demandas. Parte de esas demandas es la libertad de realizar las cuatro operaciones aritméticas básicas con símbolos arbitrarios para números desconocidos particulares. Los números que surgen a través del conteo 1,2,3,4,5,6,7,8,9,10..., son conocidos como números naturales, porque emergen más o menos de manera innata comenzando a contar las cosas desde la unidad. Este conjunto de números naturales N, se cierra bajo las operaciones de suma y multiplicación, podemos sumar dos números o multiplicarlos y el resultado siempre será un número natural. La resta, sin embargo, es un asunto diferente. La resta siendo la eliminación de un número de otro, es una operación inversa a la suma. Cuando el primer número en la operación es más pequeño que el segundo que se resta, nos expulsa de los N, por ejemplo, 5 - 15. Cuando surge este tipo de dificultad, nos damos cuenta de que este tipo de números es inadecuado y debe ampliarse para permitir la continuidad de los cálculos en un álgebra.
El modelo estándar de número que impregna todas las matemáticas e ingeniería avanzada es el campo de los llamados números complejos C. El camino desde los naturales hasta los complejos fue largo y concluyó más o menos en el siglo XIX. Pero justo después de los N, el cero como número hace su aparición, los enteros Z negativos y positivos dan paso a los racionales Q, dado que un n entero es dado por n/1. Entonces aparecen los números primos, y con estos el teorema fundamental de la aritmética que dice, la factorización prima de cualquier número natural n (con factores primos escritos en orden ascendente) es única. Esta singularidad se puede deducir de una propiedad aún más básica de los números, Euclides, dice que si un número primo p divide a un producto ab, de modo que p-ab, entonces p es un factor de a o un factor de b (o tal vez un factor de ambos). Las propiedades de los enteros y de otros números reales nos permiten crear la idea fundamental algebraica para la división el máximo común divisor.
De esta manera tropezamos con un mundo de propiedades de las que deducimos lo que podemos hacer y no con los números, y sus representaciones como símbolos dentro de las mismas reglas aritméticas exportadas al álgebra arábiga. El álgebra no es una caja de trucos para encontrar el valor de incógnitas nada más. Sino más precisamente un camino alternativo a las verdades geométricas. La notación moderna algebraica es un importante recurso para realizar cálculos más amplios en la geometría.
De las operaciones inversas a las potencias de una base particular, deducimos a los logaritmos que se convirtieron en la base de los cálculos más complejos en el siglo XVII. Y es el teorema Binomial el punto de partida algebraico para desarrollar los logaritmos y al número de Euler e.
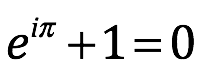
El poder algebraico proviene de la manipulación simbólica de una manera válida para todos los sistemas de ecuaciones sin importar qué número se sustituya por los símbolos. Sin embargo, cuando dividimos una expresión algebraica debemos tener cuidado de no hacerlo sobre cero, dado que al representar una incoherencia matemática, no está definida.
Ecuaciones
¿Estudiar álgebra mejora nuestra inteligencia? Mucha gente lo piensa así; sus argumentos a menudo parecen convincentes. Es cierto que las matemáticas desafían a la mente. Por ejemplo, basta con mirar a los estudiantes que luchan con demostraciones en geometría. Todos estamos de acuerdo que la matemática nos demanda esfuerzo mental. En un nivel complejo, los matemáticos son vistos como sabios y eruditos que se asoman desde el monte Olimpo. Parecen bendecidos con un orden más alto de intelecto, lo que les permite entrar en el reino de los objetos matemáticos, más allá del alcance de otros mortales. Así que no es de extrañar escuchar que el estudio de las matemáticas ampliará nuestras capacidades racionales en general, apoyando nuestro intelecto más allá de las propias disciplinas.
Augusto Comte, creía que esto era así. El álgebra fortalece la mente, dijo, permite dominar mejor el estudio de la naturaleza. En nuestro tiempo el National Council of Teachers of Mathematics, afirma que una persona que ha estudiado matemáticas debe ser capaz de vivir más inteligentemente que uno que no lo ha hecho. Las matemáticas infunden fluidez procesal, disposición productiva, comprensión conceptual, competencia estratégica y razonamiento adaptativo[1]. En una era que recompensa al pensamiento analítico, las matemáticas se consideran cruciales para el pensamiento lógico y revelan la promesa de trascender a las mentes mortales.
La matemática es una especial forma de pensamiento. Pero todo tipo de pensamiento serio implica grandes esfuerzos, como en la poesía y la música. Hay serias sospechas de que un entrenamiento del pensamiento en una esfera se acerca a pensar en otra. Ser bueno en una habilidad mental, mejora otras funciones, no importa lo similar que sean. Las matemáticas parecen ser un esfuerzo de dominio universal para la razón y la lógica. Las demostraciones matemáticas están estructuradas esquemáticamente con cada paso. Bertrand Russell ha llamado a esta lógica fría y austera, no solo por evitar a las emociones, sino por ser una búsqueda hecha por mentes altamente disciplinadas. Se asume ampliamente que la disciplina humana florecerá solo si la vida de la mente es honrada, disciplinada y flexible.
El gran objetivo de las matemáticas es probar las proposiciones. Para empezar con lo que había sido una conjetura o una hipótesis e idear pasos que las conviertan en una verdad. Establecer tales pruebas requiere mucho más que hacer un caso razonable. Para que se demuestre un teorema matemático, sus pasos deben ser tan persuasivos que aseguren lo que es esencialmente un acuerdo unánime de los miembros de la profesión. Hoy en día, las pruebas pueden correr a cientos de páginas, con frecuencia requieren la velocidad del rayo de las computadoras.
La búsqueda de demostraciones matemáticas requiere imaginación inusual, una voluntad de cuestionar las premisas prevalecientes y explorar alternativas inesperadas. Por lo tanto, perseguir pruebas en matemáticas es un ejercicio exaltado. Nos gusta cómo dice Roger Penrose:
“Una demostración en matemáticas, es un argumento impecable, utilizando solo los métodos de razonamiento lógico puro, que permiten inferir la validez de una afirmación matemática dada… de axiomas cuya validez se toma para ser evidente[2]”.
Lo que debemos subrayar es que los argumentos y los axiomas se despliegan casi en total independencia al reino de lo físico. Podemos concluir parcialmente, que el pensamiento matemático persigue pruebas. La verdad matemática, tiene poca o ninguna conexión con la búsqueda de la verdad científica; a nuestras vidas modifica su existencia. Por esta razón, proponemos que hay otras formas, más fructíferas para entender los significados y procesos de demostración, un enfoque alternativo que pueda desafiar nuestro poder mental no menos profundo que la geometría, el álgebra, el cálculo, todo lo relacionado con nuestro carácter personal de enfrentar los desafíos de la vida intelectual.
En las matemáticas y las ciencias, el avance de una teoría o del teorema, no solo depende de toda la agudeza del análisis de uno, sino de la obtención del acuerdo de sus pares. En ciencias, incluso cuando se obtiene ese veredicto, es más una deliberación tentativa que en las matemáticas. Esto se debe a que los científicos naturales enfrentan la confusión del universo profundo dentro de nuestro sesgo cognitivo. En la ciencia el consenso sobre la verdad se renueva. En las matemáticas la verdad es demostrada, se demuestra para siempre, solo sufre algunas mejoras en su elegancia. Los estudios de la ciencia intentan compartir esta certeza que dan las matemáticas, para hacer más sólido su razonamiento.
Entonces, ¿a qué nos referimos cuando decimos que se ha demostrado una teoría científica? Comencemos primero por preguntarnos lo que significa llamar cuerpo de conocimiento a una teoría. Un buen ejemplo son las ideas de Charles Darwin, que la mayoría de los científicos modernos llaman teoría de la evolución, algunos hostiles quieren que sea eliminada de las aulas, sobre los terrenos, como dicen, de que es solo una teoría. Esta frase, se expresa más como burla de ella, consideran que está destinada a trasmitir el concepto de evolución como simple especulación.
Si bien las ideas de Darwin no son la verdad última. Y por esta razón honesta, en las ciencias tomadas juntas, rara vez se alcanza el límite último de lo verdadero, quizá si lo hiciéramos ni siquiera lo sabríamos. Por lo tanto, la selección natural es el análisis más coherente que tenemos ahora mismo de cómo la vida toma las formas en la materia. Es una teoría coherente con los hechos que la sostienen, un cambio en ellos la derrumbaría exigiendo sea renovada. Así, decir que una teoría científica fue probada, significa que en su interior racional no hay contradicción lógica matemática y que guarda referencia sin contradicción también con los hechos, esos conceptos que son un consenso de las preguntas sobre lo que existe y enfrentamos en la realidad.
Si queremos que los estudiantes comprendan el proceso de demostración científica y a su hermana la verdad matemática, podríamos invitarlos a examinar cómo ha evolucionado la ciencia con los saltos agigantados del pensamiento matemático. Lidiar con las matemáticas, es considerarlas la herramienta para la búsqueda de certeza esa en la que confiaron Euclides y Pitagóras. Sí de hecho, apenas hay matemáticas a primera vista en la teoría de Darwin, que en sí valen la pena reflexionar, en sus argumentos hay proposiciones falibles, cadenas de razón creadas con proposiciones y operadores modales discursivos; pero sobre todo hay inferencias de conclusión. Las matemáticas están disueltas en el discurso científico, reflexione, quizá de ello dependa su éxito como científico, ingeniero o diseñador.
Referencias
[1] https://www.nctm.org/Standards-and-Positions/NCTM-Position-Statements/
[2] Penrose, R. (2016). The Road to Reality. Random House.