Texto académico
Autores
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Gladys Juárez Cisneros
Filho Enrique Borjas García
Lizbeth Guadalupe Villalon Magallan
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán
Unidad 4. Logaritmos
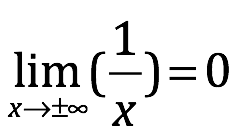El cero maya
4. Sucesiones y series
Las sucesiones son listas de términos de un conjunto en un cierto orden infinito. Es una sucesión de progresión aritmética si cada diferencia entre términos es una constante. Es una sucesión geométrica si cada término se calcula multiplicando al anterior por un número fijo o factor de n. Las series y sucesiones pueden parecer la misma cosa, pero las series son la suma o multiplicación de una sucesión empleando los símbolos 
y 
.
4.1 Sucesiones
Una secuencia o sucesión es una lista infinita de números o conjuntos que se pueden ordenar como un índice: primero, segundo, tercero…; tal como:
3,6,9,11,14…,
1,0,1,0,1,0…,
Cada elemento de la secuencia se le llama término. Un término general de una sucesión es puesto con el subíndice n. El análisis de las propiedades de una sucesión es descubrir la relación entre cada término de la secuencia: de esta manera una lista simple puede ser representada de forma general. En primer lugar, la lista tiene una coma entre cada término de la secuencia. En segundo lugar, la lista termina con puntos suspensivos “…”; este es un signo que indica sucesivamente hasta infinito. Una sucesión o secuencia siempre termina con “…” puesto que es una lista infinita. La lista solo es infinita en una sola dirección, positiva o negativa. Una lista siempre tiene un primer elemento.
Las sucesiones de números generalmente siguen patrones obvios, aunque muchas veces no son muy fáciles de identificar. Una secuencia se intenta expresar con una fórmula que sintetice la lista.
Por ejemplo:
2,4,8,10,12,14…,
Podría ser representada por:
Para abreviar podemos expresar la secuencia como 2n
Otro caso, tenga la secuencia 
donde n tiende a infinito.
La secuencia 1,0,1,0,1,0…, puede ser expresada:
Esta es una secuencia, aunque podríamos pensar en dos listas.
Las fórmulas son útiles porque dan expresiones abreviadas para secuencias de todo tipo. Traducir listas en fórmulas es algo importante para una representación perfecta de una lista infinita. Las secuencias pueden ser representadas gráficamente como un espacio de puntos.
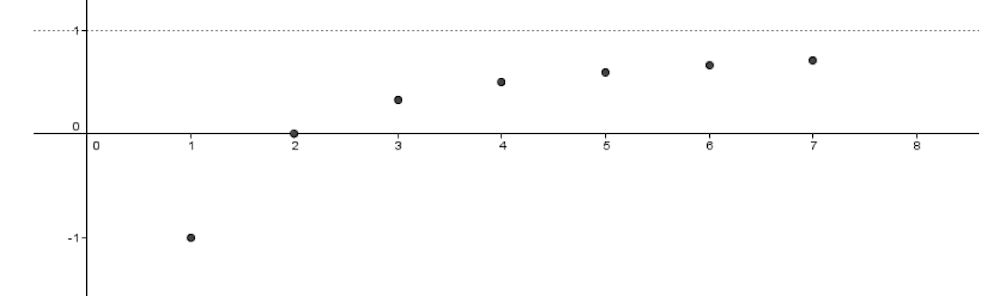
Es conveniente usar puntos en lugar de curvas para gráficos de sucesiones porque cada secuencia está definida solo para valores de números explícitamente donde interviene n.
Los gráficos son útiles para asociar una lista con el concepto matemático de función, una secuencia técnicamente es una función de números reales.
Propiedades de secuencias
Las diferentes representaciones de secuencias nos advierten de algunas propiedades. La secuencia puede ser creciente o decreciente, limitada o convergente.
Una sucesión (
) es monótona creciente si para todo n≥1 se verifica que 
, es decir, cada término es menor o igual que el siguiente.
Una sucesión (
) es monótona decreciente si para todo n≥1 se verifica que 
, es decir, cada término es mayor o igual que el siguiente.
Si las desigualdades son estrictas se dice que las sucesiones son estrictamente crecientes o estrictamente decrecientes.
Por ejemplo, la sucesión (
) = 2, 4, 6, 8, 10, 12..., es estrictamente creciente y la sucesión.
()=12, 9, 6, 3, 0, -3..., es estrictamente decreciente.
La sucesión (
)=1, -2, 3, -4, 5, -6..., no es monótona creciente ni decreciente.
Una sucesión (
) está acotada superiormente si existe un número real M tal que 
para todo n. Decimos que el número M es una cota superior de la sucesión.
Una sucesión (
) está acotada inferiormente si existe un número real M tal que 
para todo n. Decimos que el número M es una cota inferior de la sucesión.
Una sucesión (
) está acotada si lo está superior e inferiormente. En este caso, existe un número real M tal que 
para todo n.
Una secuencia 
es convergente a un límite a si y solo si, va lo suficientemente lejos a lo largo de una secuencia, nosotros podemos ver que 
se cierra a un número a.
Por ejemplo, para la secuencia:
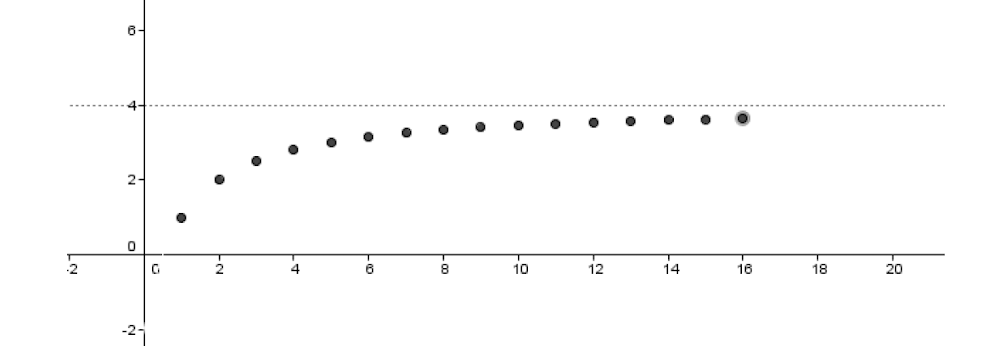
A medida que aumenta el valor de n, los valores de 
se aproximan cada vez más a 4.
Decimos que 4 es el límite de la sucesión (
) y se escribe:
Observación: El límite L de una sucesión (si existe) es único.
Una sucesión es convergente si tiene como límite un número real, y será divergente si tiene como límite +∞ o -∞.
Cualquier sucesión monótona creciente y acotada superiormente tiene límite, que es la menor de sus cotas superiores. Del mismo modo, cualquier sucesión monótona decreciente y acotada inferiormente tiene límite, que es la mayor de sus cotas inferiores.
El número “e”
Consideremos la sucesión de término general:
Sus primeros términos son:
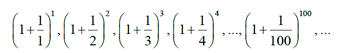
Realizando esos cálculos obtenemos:
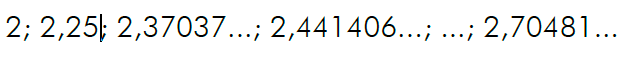
Se trata de una sucesión creciente y acotada superiormente, porque todos los términos son menores que 3.
Como vemos, los términos muy avanzados se aproximan al mismo número, el número e. Por tanto, se define el número e como:
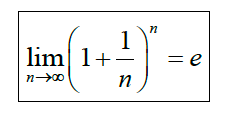
4.2 Series
Las expresiones de series infinitas se utilizan con frecuencia en matemáticas en apoyo a la ingeniería y a las ciencias, particularmente en la solución de problemas que no pueden encontrar una solución exacta o de forma cerrada. Las series infinitas son métodos que se emplean para resolver integrales, ecuaciones diferenciales y ecuaciones con derivadas parciales. Muchas funciones elementales pueden ser representadas como una serie infinita.
A la suma infinita de grandes números, de n números 
; es decir,
la podemos expresar como una serie:
Donde i es el índice de la suma, 
es el i-ésimo término de la suma y los límites superior e inferior de la suma n y 1.
El símbolo 
se le llama signo de sumatoria y es la letra sigma mayúscula del alfabeto griego. Por ejemplo:
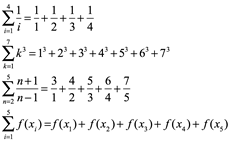
Propiedad de linealidad
- 1.
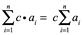
- 2.
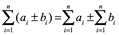
Ejemplo: Determine el valor de la sumatoria
 12.09.35.png)
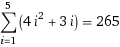
Algunas sumas notables:
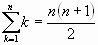
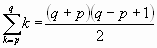
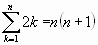
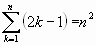
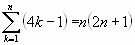
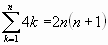
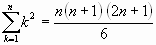
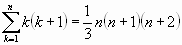
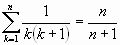
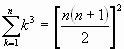
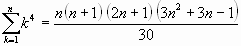
Si la sucesión de sumas parciales 
tal que 
es converge a un número real S, diremos que la serie 
converge a S. Es decir:
El número S es llamado suma o punto de convergencia de la serie.
Por ejemplo, calcúlese la suma de la serie:
Entonces:
Cancelamos los términos simétricos:
Luego por definición:
Es decir, la serie converge en 1.
Caso opuesto si la serie diverge 
:
no existe o diremos que es divergente.
4.2.1 Serie armónica
La serie de la forma:
Se le llama armónica y como veremos es divergente:
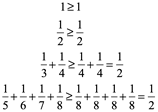
Sumamos los miembros:
De otra forma de verlo:
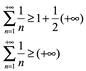
Por lo tanto, 
es divergente.
4.2.2 Serie geométrica
Una serie geométrica es construida a partir de los términos de una secuencia geométrica y se escribe como:
Es una serie de razón r y coeficiente a.
Por ejemplo, calcule el valor de:
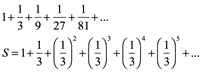
En esta serie a=1y r=1/3
Otro ejemplo, halle la suma de la serie:
La serie es geométrica de razón:
Por lo tanto, es convergente y el término inicial a=3.
Así que:
Podemos decir que converge en 6.
Otro ejemplo, analice la convergencia de:
Se observa una serie geométrica con razón (8/7)<1.
Es claro que la serie diverge.
Un ejemplo clásico es cuando la serie geométrica es negativa:
r=1/4
por lo tanto:
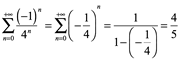
La suma de la serie converge en 4/5.
Otro ejemplo ilustrativo son los casos de sumas de series:
Desarrollando el cuadrado:
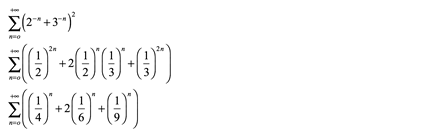
Cada una son series geométricas convergentes de:
4.2.3 Serie aritmético-geométrica
Esta serie son del tipo:
y 
están en progresión aritmética a razón de r:
Es una serie convergente.
d es una razón de la progresión aritmética y r de la progresión geométrica.
Por ejemplo, calcule el valor de convergencia de la serie:
Se transforma la expresión en:
El término (2n-1) corresponde a progresión aritmética, con:
El término 
es una progresión geométrica.
Por tanto:
4.3 Logaritmos y e
El gran matemático Euler[1], llamado por Laplace como “El maestro de todos nosotros[2]”, es quien introduce el término función en el vocabulario matemático, pareciéndose al concepto de fórmula, término relacionado con variables y constantes. La definición moderna se le atribuye al alemán Peter Dirichlet[3] quien introduce el concepto de función como una expresión, una regla o ley que define una relación entre una variable (variable independiente) y otra variable (variable dependiente).
Si observamos a nuestro alrededor, y tratamos de definir lo que ocurre, podríamos hacerlo en términos matemáticos, tal vez queda definido mediante los siguientes axiomas[4]:
a) Todo evento en la naturaleza puede ser representado mediante ecuaciones o funciones y viceversa, toda ecuación o función puede ser la representación de algún evento en la naturaleza.
b) Todo evento en la naturaleza tiene patrones.
Desde la antigüedad el hombre ha intentado buscar estas relaciones; comenzó colocando marcas en relación con el número de años o de animales que poseía. Herón de Alejandría en el siglo II D.C. encontró una fórmula que calcula el área de un triángulo en función de sus lados. Tratando de no malinterpretar a Platón[5] podría decirse que llegó a la conclusión de que los números son el lenguaje para expresar las ideas, tal vez aventurándonos pero sin poder afirmarlo podríamos pensar que ya tenía una noción de lo que es una función, de la misma forma se podría afirmar que los mayas, egipcios[6] o chinos entre otras civilizaciones ya manejaban el concepto o solamente uno cercano a él, el de relación.
Galileo[7] al relacionar el movimiento de los cuerpos celestes en función de su posición, pretendió relacionar los conceptos, formulando leyes, así dio un gran paso hacia la concepción de lo que es una función. Poco después de Galileo, Descartes muestra la relación que existe entre una gráfica y una ecuación y viceversa. Sin embargo, la definición de función se ha ido modificando con el tiempo, desde la construcción de tablas de raíces y potencias hasta como se emplea ahora. Se considera que Leibniz introduce este término, seguido por Bernoulli[8] quien en septiembre de 1694 escribe una carta en respuesta a Leibniz; lo que describe como función en el sentido más actual:
…una cantidad formada de alguna manera a partir de cantidades indeterminadas y constantes[9]…
En 1748 el concepto de función tomó énfasis gracias a la publicación “Introduction in analysin infinitorum” de Euler donde define función como:
“…una función de una cantidad variable es una expresión analítica compuesta, como cualquiera que lo sea de dicha cantidad y de números o cantidades constantes[10]…”
Así se da el crédito a Euler de precisar el concepto de función y del estudio de funciones elementales. Sin embargo, es Peter Dirichlet quien introduce el concepto moderno de función.
En este capítulo se presentan dos funciones de gran importancia, la función exponencial y la función logarítmica, que son empleadas para modelar observaciones, por ejemplo, la memoria humana[11], virus de computadora, análisis de datos: meteorología, datación por carbono, puntajes del IQ, ciencia forense e interés compuesto. De forma exponencial crecen las bacterias en un cultivo, entre muchas otras aplicaciones.
John Napier matemático escocés, en 1614 fue el primero que acuño el concepto matemático de Logaritmo[12]. Al logaritmo neperiano de base e, es llamado en honor a Napier. Henry Briggs es quien introduce la base 10 a los logaritmos.
El número exponencial e nos sirve para observar que tan rápido crecen la cosas, a menudo llamado crecimiento exponencial (es un número irracional). ¿Qué tan rápido es esto?
e= 2.718281828459045235360287471352662497757247093699...
El símbolo e fue introducido por primera vez para este número por Leonhard Euler en un artículo inédito del año 1727. Al igual que con pi, se han ideado varios métodos para tener presente los primeros dígitos de e. Por ejemplo al contar las letras de la sentencia:
In Glasgow I lectured on geometry. (2.71828)
Veamos qué tan rápido pueden crecer varias secuencias. Una forma simple de crecimiento es el tipo lineal, ilustrado por la secuencia de contenido uno a uno de números naturales 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18…; nos referimos a la secuencia para su enésimo término n.
Algo más rápido es el crecimiento cuadrático que implica los cuadrados de n2.
 15.39.15.png)
Aún más rápido resulta crecimiento cúbico, n3.
 15.54.46.png)
Todos estos son crecimientos polinomio, ya que implican potencias de n. Un crecimiento más rápido es el exponencial, donde la base es un número y n el exponencial. Por ejemplo: 3n.
 15.59.57.png)
Esta distinción entre crecimiento polinomio y exponencial la reconoció Thomas Malthus en el año 1798[13]. Su razonamiento fue que un crecimiento lineal del alimento y un exponencial de población, provocaría escasez de alimentos. De las secuencias de números anteriores, esta claro que el crecimiento exponencial es mayor que el polinomio. En procesos de control de respuesta un crecimiento polinomio es menos eficaz en su respuesta que un exponencial.
El número exponencial e está íntimamente ligado a los logaritmos, así que antes de ir más allá vamos a profundizar un poco en su naturaleza. Las primeras ideas de logaritmos (la palabra significa razón numérica de cambio), aparecieron alrededor del año 1500, cuando Nicolas Chuquet y Stifel explicaron cómo convertir ciertos cálculos que implican multiplicación y división en otros más simples que implican suma y resta. Para ilustrar esto nos apoyaremos en la secuencia de 2n.
 16.38.50.png)
Se observó que para multiplicar potencias de 2, añadimos sus exponentes. Por ejemplo, multiplicar 16 por 128, 16=24 y 128=27 nosotros escribimos:
Ahora presentamos a los logaritmos, para 
vamos escribir
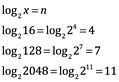
y
Estos cálculos ilustran la regla general de que el logaritmo de un producto es suma de los logaritmos separados, es decir:
Hasta ahora hemos definido estos logaritmos para potencias de 2, definiendo distintos números enteros para n. Ahora manejaremos n no entero.
Por lo general, para multiplicar a x b o más números, buscamos sus logaritmos, sumamos , y luego localizamos el número cuyo logaritmo es su suma.
Para la división podemos anotar un enfoque similar. Para dividir potencias de 2, restamos sus exponentes. Por ejemplo:
Con logaritmos:
En general la división de logaritmos:
Así que para dividir dos números buscamos sus logaritmos, restamos y luego localizamos el valor cuyo logaritmo es su diferencia. Toda esta explicación la hemos hecho con logaritmos de base 2 o también llamada potencia 2. Para otros logaritmos de cualquier base n:
En una visita Henry Briggs a Napier, cuando se conocieron, el resultado fue que Briggs comenzó a construir “Logaritmos de base 10” en los que:
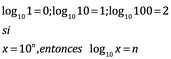
Encontró que:
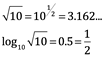
Y de nuevo cumplieron con las propiedades:
En la década de los años 1630 se crearon una serie de instrumentos mecánicos basados en escalas logarítmicas. Diseñados para ser utilizados en cálculos complicados, particularmente por astrónomos y navegantes, estos incluyeron reglas de deslizantes durante 300 años, hasta la aparición de las calculadoras electrónicas de bolsillo en 1970.
Los logaritmos fueron reconocidos rápidamente como de inmenso valor para aquellos científicos e ingenieros que necesitaban hacer cálculos extensos. Es decir con grandes números, fueron manejados en su representación más simple de logaritmos y ello implico el cálculo.
En la década de 1660 Nicolaus Mercator, independientemente de Newton y James Gregory, estaba investigando el área de bajo de la hipérbola
 10.34.20.png)
En el análisis comenzaremos por:
Se puede verificar multiplicando ambos lados por 1+x y notando que la mayoría de los términos se cancelan, dejando solo 1, o sumando la serie geométrica a la derecha. A continuación se integró esta serie infinita término a término entre 0 y 1, utilizando el hecho de que la integral de:
Para cada número k, y se obtiene una nueva serie.
Esta serie apareció para log(1+x) escrita en 1668 dada por Mercator, pero Newton ya la conocía, pero este último no se había molestado en publicarla. Es válida para todos los valores de x entre -1 y 1, y también para x=-1 cuando da:
Estos son “logaritmos de base e” pero en este momento no se especificó. En 1683 el matemático suizo Jakob Bernoulli se preocupó por los problemas de cálculo de interés. Dada una suma de dinero para invertir de tasas de interés determinada durante varios años ¿qué tan rápido crecerá? La respuesta depende de si usamos intereses simples o compuestos y de la frecuencia con que se calculan los intereses. Bernoulli quería averiguar qué pasaría si calculamos los intereses con más frecuencia, digamos n veces al año o incluso de forma continua.
Lo que hacemos para obtener los resultados es tener en cuenta que si el año se divide en n períodos, después de cada período la cantidad se multiplica por 1+(1/n), por lo que la cantidad final es:
Observamos que, a medida que n aumenta indefinidamente, estos números tienden a un valor limitante que corresponde a cuando el interés se calcula continuamente. Este valor limitante, Euler lo llamó e. Es una constante matemática e, un número irracional y será llamado a ser la base de los logaritmos naturales ln.
El número e se define como un proceso de límite, el cual Euler lo expresa en una serie:
En forma integral:
 11.27.06.png)
Así que e a la potencia 1:
Si e se eleva a la x potencia:
La mayoría de los avances en la comprensión de los logaritmos, la función exponencial y sus conexiones, se hicieron a principios del siglo XVIII. La figura principal de esta historia fue Leonhard Euler, quien investigó las principales propiedades del número exponencial e y la 
. Para e como límite.
Hemos visto que e es el límite de los números a medida que n aumenta indefinidamente, y que ex es el límite de (1+x/n)n para cualquier número x. Donde entonces e es una serie infinita:
Para cualquier potencia x elevado e:
Esta serie converge para todos los valores de x. De hecho converge por que los valores aumentan muy rápidamente. En síntesis:
La relación de funciones:
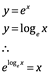
Esta relación inversa entre e y log fue observada por John Wallis en 1685 y desarrollada por Euler, quien en 1748 simplificó 
por:
A partir de aquí se le llama logaritmo natural a ln.
 12.44.28.png)
Podemos usar esta relación inversa para mostrar que para la regla de multiplicación de exponentes y para la regla básica de los logaritmos son esencialmente los mismos resultados.
Por ejemplo:
 12.50.13.png)
El logaritmo neperiano:
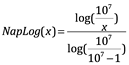
Es un cociente de logaritmos y no propiamente un logaritmo distinto en términos modernos.
Y finalmente el logaritmo de base 10 que ya hemos empleado, es también llamado logaritmo decimal.
Referencias
[1] Biografías y Vidas.revista electrónica. http://www.biografiasyvidas.com/biografia/e/euler.htm
[2] Euler(1988),Introduction to analysis of the infnite,Book I, trad. John Blandon,New York:Springer-Verlag
[3] Enciclopedia Británica. http://www.britannica.com/EBchecked/topic/165066/Peter-Gustav-Lejeune-Dirichlet
[4] Axioma: proposición tan obvia, clara y sencilla que se admite sin demostrar
[5] http://www.e-torredebabel.com/Historia-de-la-filosofia/Filosofiagriega/Platon/TeoriadelasIdeas.htm
[6] Ignacio Barradas (COMO VES)* (Fecha publicación:30/3/2005)revista electrónica (p.1)
[7] Geral James Holton, Stephen G. Brush.(1996). Introducción a los conceptos y teorías de las ciencias físicas.España:Reverté
[8] http://www.astroseti.org/articulo/4494/biografia-de-johann-bernoulli
[9] Euler, Introduction to analysis of the infinite, Book I, trns. <john Blanton, Springer-Verlag, New York, 1988,p.3.
[10] Leonhard Euler.Métodos de máximos y mínimos.España:Universidad Autónoma de Barcelona
[11] Larson Ron, Hostetler Robert (2008) Pre-calculus. USA: Reverté Ediciones, S.A. de C.V.
[12] Hobson, E. W. (2012). John Napier and the Invention of Logarithms, 1614: A Lecture by EW Hobson. Cambridge University Press.
[13] Malthus, T. R. (1927). An essay on population.