Texto académico

Autores

Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Gladys Juárez Cisneros
Filho Enrique Borjas García
Lizbeth Guadalupe Villalon Magallan
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán

Unidad 2. Álgebra arábiga

2. Introducción^[1]

Los pensadores de la Edad Media, realizaron muchas de las innovaciones matemáticas más notables, surgieron en los territorios islámicos de lo que hoy es Irak e Irán^[2]. Los estudios en esta región sentaron las bases del desarrollo del álgebra árabe, que significo: “encuentro de partes rotas”. Estos conocimientos centran las bases de la álgebra moderna, que utiliza símbolos abstractos, digamos variables x y y, para representar cantidades que pueden tomar valores numéricos y ser manipuladas matemáticamente. En este momento de la historia, se da la función de número y geometría, creando el álgebra arábiga. 

Para el devoto Kepler, Dios era el “arquitecto del universo” y lo había creado de acuerdo con un diseño para que la razón humana lo comprendiera, empleo la geometría. Un tema que Kepler consideraba divino^[3]. Para Galileo a menudo, comparaba las predicciones científicas apoyadas en matemática, como observaciones hechas sobre el mundo real. Esta insistencia le convirtió a Galileo en el padre de la ciencia moderna. Su pensamiento formo parte de una tendencia cultural, la de apuntalar la vida próspera del comercio y el arte, a través de nuevos métodos de contabilidad, cálculo y geométrica en la arquitectura. La idea más clara de considerar a las leyes fundamentales de la naturaleza expresiones matemáticas, la aporto el francés René Descartes, cuyo trabajo describió  la naturaleza y desarrollo el estilo de pensamiento objetivo, donde una supuesta relación entre los objetos que exigen, puede ser referida por un discurso a base de proposiciones. Aquí nació el lenguaje objetivo de la ciencia moderna^[4].

Pero es Newton quien crea una arquitectura matemática que involucra a los desarrollos matemáticos conocidos hasta entonces^[5]. Combina la noción de función, límite, espacio geométrico, infinito, cero maya, números reales, permitiendo hacer cálculos con infinitesimales, en la frontera de la nada y el todo. Puede que Newton jamás habría escrito “Principia” si no fuera por la influencia e iniciativa de Edmond Halley, ahora mejor conocido por el cometa que lleva su nombre en su honor.  De hecho “Principia” fue una obra correctiva de la narrativa filosófica de Descartes. Centro enteramente al mundo real, en ser descrito matemáticamente, tanto en generalidad como con precisión asombrosa. La fuera de gravedad en los planetas, Newton logro expresar a la civilización que el cielo y la tierra están gobernados por las mismas leyes de la naturaleza. Gottfried Leibniz de manera independiente también llego al cálculo infinitesimal, capaz de lidiar con cantidades físicas que no son constantes y varían continuamente en el espacio y el tiempo; convirtiendo a la técnica matemática del cálculo en la herramienta más poderosa para el desarrollo científico y de ingeniería. El razonamiento de derivadas e integrales de funciones permitió que la imaginación posterior a esta era, se aventure a través de las estrellas y los átomos con asombrosa precisión.

En nuestros días, la llegada de “x” en la escena escolar, representa para los jóvenes estudiantes el punto de partida en el que las matemáticas están más allá de la aritmética, adquiriendo un lenguaje algebraico e instalando el pensamiento superior en la idea de cuerpo cerrado bajo una operación binaria de suma y multiplicación. De aquí en adelante la ciencia moderna se basaría en sus investigaciones en el álgebra de símbolos que representan cantidades de interés. El álgebra es la herramienta a través de la cual se revelan relaciones físicas exactas, incluida la famosa ecuación E=mc². 

Existen varias álgebras, bolean, vectorial, compleja, diferencial, lineal y arábiga entre muchas otras. El álgebra sustenta la investigación sistemática moderna. Su contribución moderna en ingeniería de software sería imposible sin álgebra. Ya hemos dicho que álgebra refiere en árabe a “reencuentro de partes rotas”. Pero es la manipulación algebraica de la escritura moderna en las matemáticas, la desarrollada hasta el siglo XVII  cuando se da más luz sobre la aritmética y la existencia de papel para ensayar técnicas y métodos algebraicos. Los símbolos algebraicos X y Y, son manipulados con las leyes de la aritmética. El argumento sustenta que todo lo que hacemos con números es válido en relación a la manipulación de variables, con consecuencias, estas reglas se amplían a todas las demás álgebras por venir. 

Para aprovechar el potencial del álgebra, necesitamos ser capaces de movernos dentro de su simbología de forma desinhibida, haciéndonos libres en habilidad en su uso en operaciones de suma, resta, multiplicación, división y potencias. Para eso necesitamos un sistema numérico adecuado para el propósito. Y sin rechazar cantidades negativas y de la forma (a/b) cociente, además, de tratar a cero como un número. 

La operación matemática 3 + 2, que es la suma, es de fácil comprensión, y aún más fácil es su ejecución. A esta expresión, tres más dos lo asociamos a la idea natural que teniendo tres objetos le agregamos dos objetos, para obtener un total de cinco objetos. Lo que queremos decir con esto, que las operaciones matemáticas, por lo general, tienen una interpretación en situaciones reales. Por ejemplo, la operación 2 + 1, puede significar que tengo dos balones de futbol, y me han regalado 1 balón de futbol, lo que en total hace 3 balones de futbol.

Las matemáticas entonces, sirven para la vida real, sucede a veces, que no se puede estar estudiando caso a caso las diferentes problemáticas que se pueden resolver con las operaciones matemáticas, es entonces que se inventa un nuevo lenguaje llamado Álgebra. Esta álgebra consiste en asociar a los números las unidades que representa. Por ejemplo, la expresión tengo siete billetes de mil pesos por 7m, donde la letra m representa a un billete de mil pesos. De manera que la expresión algebraica: 7m + 5m = 12m significa, tener doce billetes de mil pesos. De igual manera, es posible que la letra m signifique un balón de futbol, entonces 7m + 5m = 12m, significa 12 balones de futbol. 

El álgebra es una rama de las matemáticas donde se consideran las cantidades de forma general, para lo cual se usan letras, generalmente las últimas del abecedario, en álgebra aparecen números, que son cantidades conocidas y letras que representan tanto a cantidades bien definidas, como a incógnitas o cantidades desconocidas. 

Por ejemplo, el peso de un cuerpo se calcula mediante la fórmula: aquí la letra representa al peso, a la masa, estas son dos cantidades desconocidas que se relacionan de manera proporcional y representa a una constante, la de la aceleración debida a la gravedad en la tierra .

2.1 Lenguaje algebraico

Para resolver problemas matemáticos por medio del álgebra es necesario traducir del lenguaje común al lenguaje algebraico. A continuación, se muestran algunos ejemplos de expresiones en lenguaje común traducidas a lenguaje algebraico:

Un número cualquiera=

El doble de un número=

La tercera parte de un número=

La diferencia entre dos números=

El cuadrado de la suma de dos números distintos=

El producto de la suma por la diferencia de dos números=

El cuadrado del doble de un número menos el triple de otro=

Un número más su consecutivo=

Al traducir encontramos palabras claves como doble que lo traducimos como multiplicar por dos, la tercera parte, dividir entre tres, la diferencia equivale a la resta, el cuadrado de a, elevar a la potencia dos, el producto a la multiplicación.

Términos en álgebra^[6]

Es cada parte de una expresión algebraica cuando estos están separados por un signo. La parte numérica de un término que contiene una variable se llama coeficiente de la variable.

Término algebraico semejante

Los términos algebraicos semejantes son aquellos que contienen las mismas variables, tales como 7x y 11x o como 3a y 7a. Un término sin una variable se llama constante (una constante es una expresión que tiene un valor fijo). Los términos constantes también se llaman términos semejantes.

Término algebraico y sus partes

Una expresión algebraica es una combinación de números y símbolos (que representan números) unidos por las operaciones elementales como la suma, resta, multiplicación y división.

Por ejemplo: 9x⁵y, son expresiones algebraicas

Un término es una expresión algebraica que no está separada por el signo más ni por el signo menos.

Por ejemplo:  5pq, -234abcd,

Grado absoluto de un término algebraico^[7]

El grado de un término es la suma de los exponentes de las variables

Ejemplo: su grado absoluto es 3+5=8

Propón la siguiente adivinanza a un amigo:

1. Piensa un número 
2. Multiplícalo por 2
3. Añade 4 al resultado
4. Al resultado anterior multiplícalo por 3
5. Resta doce al resultado anterior
6. Divide lo obtenido entre 6
7. Réstale el número que pensaste

¡Te quedó cero!

Si llamamos al número inicial, podemos escribir las expresiones algebraicas que obtenemos en cada paso:

Como ves, podemos resolver problemas manejando expresiones algebraicas. A estas letras se les llama incógnitas, o indeterminadas (por norma, las letras se ordenan alfabéticamente). 

Por ejemplo: 3x²+6xy+3y²

Las expresiones algebraicas nos permiten traducir el lenguaje ordinario.

Una expresión algebraica está en forma reducida o simplificada si no tiene términos semejantes ni paréntesis, esto se llama reducción o simplificación de términos de una expresión.

Ejemplo: reducir la expresión 8(x+5).

8(x+5) = 8(x)+8(5) =8x+40 

Reduce -3t+11-4t

Los términos semejantes son -3t y –4t

-3t+11-4t = 11-3t-4t = 11-7t

En la siguiente expresión algebraica 5y+4+6y. 

Identifica los términos, términos semejantes, constantes, coeficientes y factores; una vez identificada la estructura de la expresión simplifícala. 

Términos: 5y, 4, 6y

Términos semejantes: 5y, 6y

Constantes: 4

Coeficientes: 5, 6

Factores: 4, 5, 6, y

Expresión algebraica simplificada: 11y+4  

Tipos de expresiones algebraicas^[8]

1. Monomio: es una expresión algebraica formada por un solo término, como 4x, 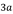, , 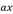 ,  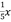, , , 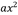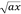etc.
2. Binomio: es una expresión algebraica formada por dos términos, como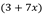, (3a+4x), 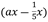,,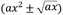 etc.
3. Trinomio: es una expresión algebraica formada por tres términos, como 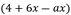, , 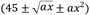etc.
4. Polinomio: es una expresión algebraica formada por dos términos o más.

                          Los binomios y trinomios son polinomios con nombres especiales.

Clasificación de expresiones algebraicas^[9]

Las expresiones algebraicas se pueden clasificar en función del tipo de operaciones que afectan a su parte literal en: enteras, racionales, e irracionales.

1. I. Expresión algebraica entera: es aquella en la cual no hay ninguna letra en el denominador. En el caso contrario, dicha expresión algebraica se llama fraccionaria.

Ejemplo: etc.

1. II. Expresión algebraica racional: es aquella en la cual no hay ninguna letra bajo un signo radical. En caso contrario, la expresión algebraica correspondiente recibe el nombre de irracional. 

1. Expresiones algebraicas racionales: son términos que no tienen literal en el denominador. 

Ejemplo: , , , etc

b) Expresión algebraica fraccionaria: son términos que tienen parte literal en el denominador.

Ejemplo:, ,etc.

1. III. Expresión algebraica irracional: son términos que poseen radicales.

Ejemplo:, ,

Valor numérico de una expresión algebraica^[10]

Valor numérico de una expresión algebraica es el resultado que se obtiene al efectuar las operaciones indicadas después de haber sustituido las letras por números, a cada letra, un número único que puede ser el mismo para diferentes letras, pero no puede ser distinto para la misma letra en posiciones distintas.

El valor numérico de una expresión algebraica depende de los valores atribuidos a sus letras. Una expresión algebraica puede tener diversos valores numéricos al variar los valores atribuidos a las letras.

Ejemplo:

Para

Equivalencia de expresiones algebraicas

Son aquellas expresiones que tienen el mismo valor para todas las sustituciones permisibles. Por ejemplo, algebraicamente x+2x=3x, por lo que estas dos expresiones son equivalentes.

Otro ejemplo son las expresiones 3(+4) y 3+12, son expresiones equivalentes, porque tienen el mismo valor sin importar cuál sea el valor de .

2.2 Operaciones algebraicas^[11] 

Las cuatro operaciones básicas que se pueden realizar con las expresiones algebraicas enteras son suma, resta, multiplicación y división. 

Suma

Las sumas de expresiones algebraicas enteras se efectúan mediante la agrupación de términos semejantes. Solo se pueden sumar monomios y el resultado es otro monomio.

Ejemplo:

Otra forma en que comúnmente se realizan las sumas es de la siguiente manera:

Como podemos ver, se quitaron primero los paréntesis y después se agruparon los términos semejantes. La suma se puede realizar con más de dos expresiones algebraicas, por ejemplo, podemos sumar 3x + 4y con 2x + 5y y 4y, como podemos observar en la última expresión, a diferencia de las otras dos, no se encuentra ningún término con la variable x, sin embargo, la operación se puede realizar como veremos:

Con la práctica las operaciones se hacen de manera inmediata sin tener que escribir las agrupaciones, sin embargo, el llevar a cabo las agrupaciones ayuda  a adquirir la confianza en las operaciones.

Resta

La resta de dos operaciones algebraicas se realiza de manera similar a como se hace con la suma de operaciones algebraicas, es decir, se realizan las restas entre dos términos semejantes.

Ejemplo: restar 2x+2y de x–y.

Restar 2x²+2y+z de x²+2y.

(x²+2y)-(2x²+2y+z)=x²+2y-2x²-2y-z=(x²-2x²)+(2y-2y)+z=-x²-z

Multiplicación

La multiplicación de dos polinomios se efectúa multiplicando todos y cada uno de los términos de uno de ellos por todos y cada uno de los términos del otro y sumando todos los productos obtenidos, reduciendo términos semejantes, el resultado de la suma de estos productos genera un nuevo polinomio. Generalmente se ordenan ambos polinomios en orden creciente o decreciente.

La multiplicación se realiza de la forma siguiente:

1. a) Se realiza la multiplicación como ya se describió de los coeficientes A por B, si es un entero se escribe directamente en el resultado, si por el contrario, no lo es, se acostumbra dejarlo como fracción.
2. b) Si tienen las mismas variables ambos polinomios, se aplican las propiedades de los exponentes  para expresar las variables con sus respectivas potencias en el resultado.

Multiplicar los siguientes monomios: 4x por 6

Multiplicar los siguientes monomios 4x por 6x.

Multiplicar el monomio 6 por el binomio 4x+6.

Multiplicar el monomio 3x por el binomio 4x-6y.

Multiplicar el monomio 3x² por el binomio -4x-6y.

Multiplicar el binomio 3x²+3 por el binomio 4x-6y.

Se ordena el polinomio resultante alfabéticamente, así como el grado de forma decreciente:

(4x-6y) (3x²+3) = 12x³-18x²y+12x-18y

Multiplicar el trinomio x²+2x–1 por  el siguiente trinomio de grado dos x²+2x+1

División

La división se realiza de la forma siguiente:

1. Se realiza la división de los coeficientes A entre B, si es un entero se escribe directamente en el resultado, si por el contrario, no lo es, se acostumbra dejarlo como fracción.
2. Si tienen las mismas variables ambos polinomios, se aplican las propiedades de los exponentes para expresar las variables con sus respectivas potencias en el resultado.
3. Si no son iguales las variables del numerador con las del denominador, generalmente se dejan como aparecen, aunque también se pueden  expresar las variables  del numerador subiéndolas al numerador con potencias negativas.

1. División de dos monomios: la división de dos monomios se encuentra hallando el cociente de los coeficientes y el de las variables, el resultado es el producto de los cocientes de los coeficientes por el de las variables.

Ejemplo: dividir 32xy² entre 2xyz

Dividir: 32xy²z entre 2xyz

II. División de un polinomio entre un monomio: se realiza dividiendo cada termino del polinomio entre el monomio y luego se simplifica la expresión algebraica.

Dividir a²+b entre

Dividir a²+b+c entre d

Dividir 2x⁵yx+3x³y²z+xy²z² entre xyz

III. División entre polinomios: para la división de dos polinomios (por la división larga), se emplea una serie de pasos que mediante el siguiente ejemplo se describirán:

Dividir 2+1+² entre 1+

1. Se ordenan los términos de ambos polinomios según las potencias decrecientes (o crecientes) de una de las letras comunes a los dos polinomios. ²+2+1 y +1

b) Se divide el primer término del dividendo  por el primero del divisor, con lo que resulta el primer término del cociente.

c) El primer término del cociente se multiplica por el divisor, para después restar este producto del dividendo.

d) Una vez realizada esta resta, ahora se centra la atención en este resultado (1er residuo parcial),  el cual es un monomio  que se completa a un polinomio con un número de términos similares a los del divisor y para lo cual se bajan los términos siguientes necesarios del  dividendo. Este polinomio recién formado se divide entre el divisor para formar el segundo término del cociente.

e) El divisor se multiplica por el 2º término del cociente, para después restar este producto del polinomio recién formado. Realizar esto de manera consecutiva hasta reducir el residuo a cero o a un polinomio de grado y extensión menor que el divisor.

f) Si el residuo es cero, entonces el cociente y el divisor son factores del dividendo.

También es posible presentar la operación de manera racional:

Como podrás darte cuenta la división larga se parece mucho a las divisiones aritméticas.

División sintética

Si el divisor es un polinomio de primer grado de la forma x–c donde c es una constante, esta constante puede ser inclusive un número complejo, sin embargo, aquí c es una constante real. Ahora explicaremos la división sintética, realizando de manera paralela el ejercicio anterior. El algoritmo de la división sintética se realiza de acuerdo a los pasos que se desarrollaran en el siguiente ejemplo:

Aplica la división sintética para dividir ²+2+1 entre +1.

Recordar que el divisor es+1 y el dividendo es ²+2+1

1. Listar los coeficientes del dividendo en orden decreciente de potencias de x, escribiendo 0 para cada potencia de x que falte.

b) Colocar como prefijo de esta lista al valor de x que hace cero al divisor. 

En este caso el prefijo es x=–1, que proviene del divisor cuando este lo hacemos cero; es decir: x+1=0 y la solución en x se encuentra despejando x x=–1.

c) Escribir en la parte inferior el coeficiente principal de la lista, multiplicarlo por el prefijo y sumar el producto al siguiente coeficiente de la lista. 

d) Multiplicar por el prefijo la suma obtenida en el paso anterior  y sumar el producto al siguiente coeficiente. Repetir este paso hasta haber usado todos los coeficientes de la lista.

g) Todos los elementos del tercer renglón excepto el último son los coeficientes del polinomio cociente, en orden decreciente de potencias, se comienza por una potencia menor a la que tiene el dividendo. El último elemento de este renglón es el residuo. Si el residuo es cero, entonces el cociente y el divisor son factores del dividendo.

Dividendo = ²+2+1 y es de grado 2, el cociente de la división debe ser un grado menos, o sea, de grado 1, y el residuo es igual a cero; esto es:

Comparación de un ejercicio por división larga y división sintética:

Encontrar el cociente entre 2x³–5x²+3x+1 y  x–3 por el algoritmo de la división larga y por división sintética.

Como podemos ver el residuo es diferente de cero, entonces el cociente y el divisor son factores del dividendo más el residuo resultante; esto es: 

2x³–5x²+3x+1 = (2x²+x+6) (x–3)+19

También es posible presentar la operación de manera racional:

Las 4 operaciones básicas que se pueden realizar con las expresiones algebraicas racionales son las mismas que se analizaron con expresiones algebraicas enteras.

Suma

Las sumas de expresiones algebraicas racionales se efectúan mediante la agrupación de términos semejantes. Solo se pueden sumar monomios y el resultado es otro monomio.

Sumar 

Efectúa la siguiente operación:

Primero se evalúa el mcm (máximo común múltiplo) de los denominadores:

mcm =

Segundo, se resuelve el primer término de la expresión algebraica racional, para lo cual, el mcm se divide por el denominador de la primera fracción:

Tercero, el cociente de la división se multiplica por el numerador de dicha fracción:

Y así se resuelve cada término.

Para el 2º término:

Para el 3er. término:

La operación quedaría así:

Se agrupan los términos semejantes, eliminando los que sean iguales pero de diferente signo.

Ordenando por grado:

Resta

Para la resta de expresiones algebraicas racionales se presentan los mismos casos que para la suma y su solución es la misma, únicamente se prevé el cambio del signo más (+) por el de menos (–).

Multiplicación

El producto de expresiones algebraicas racionales se realiza al igual que como se estudió en las operaciones básicas con expresiones algebraicas enteras. En la multiplicación  de fracciones, el numerador es el producto de los numeradores y el denominador es el producto de los denominadores de las fracciones dadas, pero en este caso en particular se factorizan^[12] y se simplifican^[13], como se describe a continuación en el siguiente ejemplo.

Realizar el siguiente producto.

Factorizar lo que sea posible del numerador y denominador de cada término de la expresión algebraica:

Realizar el siguiente producto:

Factorizar lo que sea posible del numerador y denominador de cada término de la expresión algebraica.

Se sustituyen estos valores en la expresión algebraica original.

División

Para dividir dos expresiones algebraicas fraccionarias, es suficiente con multiplicar la primera con el inverso de la segunda y luego se reducen términos semejantes resultantes del producto.

Efectúa la siguiente división. 

Efectúa la siguiente división:

Se realizan las factorizaciones pertinentes de acuerdo a recomendaciones de ejemplos del tema anterior y se reducen términos semejantes.

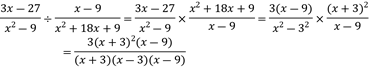
Simplificación de expresiones algebraicas racionales

a) De ser posible se factoriza^[14] el numerador y denominador de la fracción.

b) Se reducen términos semejantes resultantes de la factorización del paso anterior

Ejemplo: simplifica la siguiente expresión algebraica:

Se realizan las factorizaciones pertinentes tanto en el numerador como en el denominador de la fracción y se reducen términos semejantes.

Simplificar la siguiente expresión algebraica:

Se realizan las factorizaciones pertinentes tanto en el numerador como en el denominador de la fracción y se reducen términos semejantes.

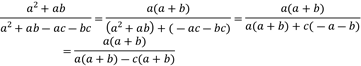
Potencia de expresiones algebraicas enteras y racionales

La exponenciación es una multiplicación de varios factores iguales, es decir, una multiplicación  abreviada, y para evaluarla es suficiente con aplicar la regla de multiplicación tantas veces como lo indique el exponente.

Ejemplo: evalúa la potencia de la siguiente exponencial con base polinomial entera.

Evalúa la potencia de la siguiente exponencial con base polinomial entera.

Evalúa la potencia de la siguiente exponencial con base polinomial entera.

Se eliminan términos semejantes (si los hay) y se ordenan de acuerdo al grado y alfabéticamente.

El resultado se multiplica una vez más por la base de la exponencial porque el exponente de la misma es 3.

Finalmente se eliminan términos semejantes (si los hay) y se ordenan de acuerdo al grado y alfabéticamente.

Evalúa la potencia de la siguiente exponencial con base polinomial racional.

Operaciones básicas con expresiones algebraicas racionales.

Sustituir en expresión original:

Se simplifica:

Radicales de polinomios^[15]

Raíz cuadrada de polinomios enteros.

Para extraer la raíz cuadrada de una expresión algebraica entera se aplica el siguiente método que se detallará a través del ejemplo a continuación:

Evalúa la raíz cuadrada de

a) Se ordena el polinomio dado:  

b) Se halla la raíz cuadrada del primer término del polinomio, que será el primer término de la raíz cuadrada; se eleva al cuadrado esta raíz y se resta al polinomio.

c) Se bajan los dos términos siguientes del polinomio y se divide el primero de estos por el duplo del primer término de la raíz. El cociente es el segundo término de la raíz. Este segundo término de la raíz con su propio signo se escribe al lado del duplo (multiplicar por 2) del primer término de la raíz y se forma un binomio; este binomio se multiplica por dicho segundo término y el producto se resta de los dos términos que habíamos bajado.

d) Se bajan los términos necesarios para tener tres términos en el residuo. Se duplica la parte de la raíz ya hallada (1er y 2º término de la raíz) y se divide el primer término del residuo entre el primero de este duplo. El cociente es el tercer término de la raíz. Este tercer término con su propio signo, se escribe al lado del duplo de la parte de la raíz hallada y se forma un trinomio; este trinomio se multiplica por dicho tercer término de la raíz y el producto se resta al residuo.

e) Se continua el procedimiento anterior, dividiendo siempre el primer término del residuo entre el primer término del duplo de la parte de la raíz hallada, hasta obtener residuo cero.

f) Si el residuo es cero, entonces la potencia de la exponencial cuadrada de la raíz es el radicando de la radicación.

Raíz cuadrada de polinomios racionales

Prácticamente se emplea la misma metodología del caso anterior, teniendo presente de simplificar cada vez que se pueda.

Nota: La raíz cuadrada de un polinomio racional con denominadores que contengan literales, puede extraerse enviando las letras al numerador cambiándole el signo a sus exponentes.

La extracción de la raíz cuadrada de una expresión algebraica racional se comprenderá mejor a través del ejemplo a continuación:

Ejemplo: evalúa la raíz cuadrada de 

b)

c)

d)

e) Si el residuo es cero, entonces la potencia de la exponencial cuadrada de la raíz es el radicando de la radicación.

Raíz cúbica de polinomios enteros 

Para extraer la raíz cúbica de una expresión algebraica entera, se aplica el siguiente método que se detallará a través del ejemplo a continuación:

Hallar la raíz cúbica de

a) Se ordena el polinomio dado:

b) Se extrae la raíz cúbica de su primer término, que será el primer término de la raíz; este término se eleva al cubo y se resta del polinomio.

c) Se bajan los tres términos siguientes del polinomio y se divide el primero de ellos por el triplo (multiplicar por 3) del cuadrado del término ya hallado de la raíz; el cociente de esta división es el segundo término de la raíz.

d) Se forman tres productos: 1º.- El triplo del cuadrado del primer término de la raíz por el segundo término de la raíz. 2º.- El triplo del primer término de la raíz por el cuadrado del segundo término de la raíz. Y 3º.- Cubo del segundo término de la raíz. Estos productos se restan (cambiándole los signos) de los tres términos del polinomio que se habían bajado (residuo).

e) Se bajan los términos que faltan del polinomio y se divide el primer término del residuo entre el primer término del triplo del cuadrado de la raíz ya hallada. El cociente de esta división, es el tercer término de la raíz. Se forman tres productos: 1º.- Triplo del cuadrado del binomio que forman el primer y segundo término de la raíz por el tercer término de la raíz. 2º.- Triplo de dicho binomio por el cuadrado del tercer término de la raíz. y 3º.- Cubo del tercer término de la raíz. Estos productos se restan (reduciendo previamente términos semejantes si los hay) del residuo de la raíz. Si la diferencia es cero, la operación ha terminado. Si aún quedan términos en el residuo, se continúa el procedimiento anterior hasta obtener residuo cero.

f) Si el residuo es cero, entonces la potencia de la exponencial cúbica de la raíz es el radicando de la radicación.

Raíz cúbica de polinomios racionales

Prácticamente se emplea la misma metodología del caso anterior, teniendo presente de simplificar cada vez que se pueda.

La extracción de la raíz cúbica de una expresión algebraica racional se comprenderá mejor a través del ejemplo a continuación:

Hallar la raíz cúbica de:

a)

b)

c)

d)

e)

f) Si el residuo es cero, entonces la potencia de la exponencial cúbica de la raíz es el radicando de la radicación.

2.3 Productos notables de expresiones algebraicas^[16]

Es como se les define a las multiplicaciones con expresiones algebraicas donde el producto puede ser señalado como regla constante, sin verificar dicha multiplicación. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.

Cada producto notable se relaciona a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados.

Binomio con término común

En un producto de dos binomios que tienen un término común, se suma el cuadrado del término común con el producto del término común por la suma de los otros términos no comunes y posteriormente se añade el producto de los términos no comunes.

Ejemplo:

La siguiente figura muestra el producto de binomios con un término común:

Ejemplo:  desarrolla el siguiente producto:

Binomios conjugados

Dos binomios conjugados son aquellos que solo difieren en el signo de la operación. El resultado de un producto de binomios conjugados es igual a la diferencia de cuadrados de cada término.

Ejemplo:

La siguiente figura muestra el producto de binomios conjugados:

Desarrolla el siguiente producto:

Binomio al cuadrado

Para elevar un binomio aditivo al cuadrado, es decir, multiplicarlo por sí mismo, es suficiente con elevar el primer término al cuadrado, sumar el doble producto del primer término por el segundo término y finalmente sumar el cuadrado del segundo término. Si el binomio es una diferencia se alternan los signos empezando con el primer término con signo positivo, el segundo con signo menos y el tercer término con signo positivo.

Ejemplo:

La siguiente figura muestra un binomio al cuadrado:

Desarrollar:

Desarrolla el siguiente binomio al cuadrado:

Binomio al cubo

Para elevar un binomio aditivo al cubo, es decir, multiplicarlo por sí mismo tres veces, es suficiente con elevar el primer término al cubo, sumar el triple producto del primer término al cuadrado por el segundo término, adicionarle el triple producto del primer término por el cuadrado del segundo término y finalmente sumarle el segundo término al cubo. Si el binomio es una diferencia se alternan los signos, empezando con el primer término con signo positivo, el segundo con signo negativo, el tercer término con signo positivo y el cuarto y último término negativo.

Ejemplo:

La siguiente figura muestra un binomio al cubo:

Ejemplo: mediante la técnica del binomio al cubo, localiza la potencia de la siguiente exponencial al cubo:

Mediante la técnica del binomio al cubo, desarrolla la potencia de la siguiente exponencial al cubo: 

Binomio de Newton

El teorema del binomio^[17], descubierto hacia 1664 -1665, fue comunicado por primera vez en dos cartas dirigidas en 1676 a Henry Oldenburg (hacia 1615-1677), secretario de la Royal Society que favorecía los intercambios de correspondencia entre los científicos de su época. En la primera carta, fechada el 13 de junio de 1676, en respuesta a una petición de Leibniz que quería conocer los trabajos de matemáticos ingleses sobre series infinitas, Newton presenta el enunciado de su teorema y un ejemplo que lo ilustra, y menciona ejemplos conocidos en los cuales se aplica el teorema. Leibniz responde, en una carta fechada el 17 de agosto del mismo año, que está en posesión de un método general que le permite obtener diferentes resultados sobre las cuadraturas, las series, etc., y menciona algunos de sus resultados. Interesado por las investigaciones de Leibniz, Newton le responde también con una carta fechada el 24 de octubre en la que explica en detalle cómo ha descubierto la serie binómica. 

El descubrimiento de la generalización de la serie binómica es un resultado importante de por sí; sin embargo, a partir de este descubrimiento Newton tuvo la intuición de que se podía operar con series infinitas de la misma manera que con expresiones polinómicas finitas. El análisis mediante las series infinitas parecía posible, porque ahora resultaban ser una forma equivalente para expresar las funciones que representaban. 

Newton no publicó nunca el teorema del binomio. Lo hizo Wallis por primera vez en 1685 en su álgebra, atribuyendo a Newton este descubrimiento.

Como sabemos, de los temas de factorización anteriores, podemos desarrollar fácilmente polinomios de la forma a² + 2ab + b² o  a³ + 3a²b +3ab² + b³ , sin embargo, el realizar operaciones con potencias de mayor grado resulta tedioso, a continuación presentamos algunos de ellos: 

(a + b)¹ = a + b 

(a + b)² = a² + 2ab + b²

(a + b)³ = a³ + 3a²b +3ab² + b³

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ 

(a +b)⁵ =  a⁵ + 5a⁴b +10a³b²+ 10a²b³ + 5ab⁴ + b⁵ 

Es de la forma^[18] y una forma fácil de determinar sus coeficientes numéricos al desarrollarlo es mediante el triángulo de Pascal, el cual se construye de acuerdo a las instrucciones siguientes sin llegar al término general.

Primero empezar cada renglón con 1 y terminarlo en 1. Los números restantes son la suma de los dos números situados inmediatamente arriba a la izquierda y a la derecha.

Segundo, con respecto a los términos algebraicos que incluyen las literales a y b, la suma de los exponentes de a y de  b en cada término es igual al exponente del binomio, es decir, cuando disminuye el exponente de a, aumenta el de b; ambos en una unidad.

Donde:

1. 1. n = entero positivo.
2. 2. Signos:

1. a) En 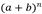  todos los signos son positivos. 

Ejemplo:

1. b) En 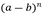  se empieza con  +  y luego se van alternando.

Ejemplo:

Ejemplo: evalúa la potencia del siguiente binomio aplicando el triángulo de Pascal.

Se hace y y se aplica la regla según triángulo de pascal. 

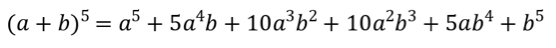
Se sustituyen datos y se resuelve.

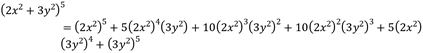
Por último, simplificar la expresión haciendo uso de las leyes de exponenciación.

2.4 Factorización^[19]

Como ya se analizó en los números racionales existen otros números que se expresan como el producto de otros a los que les llamamos factores que, al multiplicarlos todos, resulta el número original^[20]. En el caso particular de los números, los factores son números primos, en álgebra, la factorización es expresar un polinomio como producto de otros polinomios a los que les denominaremos factores al igual que con los números.

Factor común

El factor común es la literal común de un binomio, trinomio o polinomio, con el menor exponente y el divisor común de sus coeficientes.

La figura que representa la regla del factor común es la siguiente:

Reglas para extraer el o los factores comunes de expresiones algebraicas

a) Factor común monomio: se extrae por agrupación de términos.

Extraer de la siguiente expresión el factor común.

Extraer de la siguiente expresión el o los factores comunes.

b) Factor común polinomio: primero hay que determinar el factor común de los coeficientes junto con el de las variables de menor exponente. Aquí el factor común no cuenta con un término, sino con dos.

Extraer de la siguiente expresión el o los factores comunes:

Extraer de la siguiente expresión el o los factores comunes:

Diferencia de cuadrados

Son binomios cuyos términos están al cuadrado y los signos de cada uno son diferentes. Los términos se caracterizan por tener raíz cuadrada exacta.

La factorización de la diferencia de cuadrados consiste en obtener la raíz cuadrada de cada término y representar estas como el producto de binomios conjugados tal y como se estudió en el tema: Binomios conjugados de este apartado, a continuación, se muestra tal expresión:

Ejemplo: resuelve la siguiente diferencia de cuadrados.

Resuelve la siguiente diferencia de cuadrados.

Trinomio cuadrado perfecto

Son aquellas expresiones algebraicas de tres términos, de los cuales dos tienen raíces cuadradas exactas, y el resto equivale al doble producto de las raíces cuadradas del primero por el segundo. De hecho, es la operación inversa al  desarrollo de un binomio al cuadrado.

Para factorizar se ordenan los términos dejando de primero y de tercero los términos cuadráticos, luego extraemos la raíz cuadrada del primer y tercer término y los escribimos en un paréntesis elevado al cuadrado, separándolos por el signo que acompaña al segundo término. Por último, se verifica que el doble producto del primero por el segundo término sea 2ab, con lo que se confirma que es correcta la solución. De ser diferente esta solución no es la correcta. La expresión algebraica que manifiesta esta regla es:

Ejemplo: factoriza el siguiente trinomio cuadrado: 

Verificando

la factorización es correcta.

Factoriza el siguiente trinomio cuadrado: 

Verificando

la factorización es correcta.

Trinomio de la forma

Son aquellas expresiones algebraicas de tres términos, donde hay una variable^[21] cuadrática, una lineal y un término independiente. Se resuelve por medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la variable cuadrática, buscando dos números que multiplicados den como resultado el término independiente y sumados (pudiendo ser números negativos) den como resultado el término del medio. Cuando el coeficiente numérico de la variable cuadrática sea diferente de uno, es decir, , multiplicar el trinomio por :

En esta expresión resultante hay que precisar la siguiente observación: Después de multiplicar por , el término central se deja expresado así y cuando se obtengan los dos paréntesis resultantes de la factorización dividir ambos entre . Si no divide a ningún coeficiente numérico de los términos da la factorización, se descompone en sus factores y se vuelve a intentar una vez más la división.

Factoriza el siguiente trinomio:

Debo buscar dos números cuya diferencia me dé 2 y cuyo producto me dé 15.

Factoriza el siguiente trinomio:

Debo buscar dos números cuya suma me dé 5 y cuyo producto me dé 6.

Factoriza el siguiente trinomio:

En esta expresión , por lo que se debe multiplicar toda la expresión por el coeficiente del término cuadrático que es 6.

Debo buscar dos números cuya resta me dé 7 y cuyo producto dé 18.

Como al inicio se multiplicó por 6, ahora debemos dividir también entre 6 para no afectar la expresión algebraica en su totalidad.

Se observa que algunos términos del producto de los binomios resultantes de la factorización no son divisibles por 6, así que descomponemos 6 en sus factores, esto es, 6=3x2.

Factorización por agrupación

Para factorizar por agrupación de términos un polinomio, debe considerase los términos comunes y posteriormente los compuestos resultado de la primera agrupación donde se aplica el caso del factor común. La expresión algebraica que representa este tipo de factorización es la siguiente:

Ejemplo: factoriza la siguiente expresión algebraica.

Polinomio cubo perfecto

Son aquellas expresiones algebraicas de 4 términos, de los cuales dos tienen raíces cúbicas exactas, y el resto equivale al triple producto del primer término al cuadrado por el segundo término y al triple producto del primer término por el cuadrado del segundo término. De hecho, es la operación inversa de un binomio al cubo. La expresión algebraica que representa esta regla es:

Para factorizar^[22] se siguen los siguientes pasos:

1. Debe tener cuatro términos y estar ordenado con respecto a una letra. 
2. Dos de sus términos, el 1º (a³) y el 4º (b³), deben poseer raíz cúbica exacta. 
3. El segundo término debe ser igual al triple producto del cuadrado de la raíz cúbica del primer término por la raíz cúbica del cuarto término 3a²b. 
4. El tercer término debe ser igual al triple producto de la raíz cúbica del primer término por el cuadrado la raíz cúbica del cuarto termino 3ab². 
5. El segundo y el cuarto término deben tener el mismo signo y puede ser positivo o negativo, el primer y tercer término siempre son positivos (si el primer y tercer término son negativos realizar factor común con el factor -1). 
6. Si todos los términos son positivos el resultado es el cubo de la suma de dos cantidades (a + b)³, si hay términos negativos el resultado es el cubo de la diferencia de dos cantidades (a – b)³. 

Ejemplo: factorizar la siguiente expresión algebraica

Paso 1:                      

Paso 2:  

donde

Paso 3:

Paso 4:

Paso 5:

Del paso 1 se observa que el segundo y el cuarto término tienen el mismo signo y es positivo, al igual que el primer y tercer término.

Paso 6:

Como todos los términos son positivos, el resultado es el cubo de la suma de dos cantidades (a + b)³, por tanto:

Factorizar la siguiente expresión algebraica:

Paso 1:

Paso 2: 

donde

Paso 3:

Paso 4:

Paso 5:

Del paso 1 se observa que el segundo y el cuarto termino tienen el mismo signo y es negativo.

Paso 6:

Como hay términos negativos, el resultado es el cubo de la diferencia de dos cantidades (a–b)³, por lo tanto:

Binomio de la forma^[23]

Abordaremos estas expresiones algebraicas de acuerdo a lo siguiente:

Sean las expresiones     y  

      y      

Así el dividendo es igual al divisor multiplicado por el cociente, como a continuación se muestra:

        y       

De donde se deducen las siguientes reglas:

1. La suma de dos cubos perfectos se descompone en dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz. 
2. La diferencia de dos cubos perfectos se descompone en dos factores, el primero es la diferencia de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz más el producto de ambas raíces más el cuadrado de la segunda raíz. 

Ejemplo: factorizar la siguiente diferencia de cubos:

Como se aprecia, es una diferencia de cubos y se aplica la regla 2, 

1. Se extraen las raíces cúbicas de los términos de la diferencia de cubos

.   y.   

b) Se sustituyen datos en la regla principal:

c) Se reducen términos.

Factorizar la siguiente suma de cubos:

Como se aprecia, es una suma de cubos y se aplica la regla 1, 

a) Se extraen las raíces cubicas de los términos de la diferencia de cubos.

    y       

b) Se sustituyen datos en la regla principal.

c) Se reducen términos,

2.5 Expresiones algebraicas racionales^[24]

En una expresión algebraica racional donde el denominador implica radicales, al proceso por el cual se determina otra expresión algebraica que no involucra radicales en el denominador y que es equivalente a la expresión algebraica dada; se le llama racionalización del denominador de dicha expresión. Este proceso facilita el cálculo de operaciones como la suma de fracciones.

Consecuentemente, racionalizar el denominador de una fracción es transformarlo en un número racional. Para esto se multiplican los dos términos por una expresión que convierta al denominador en potencia perfecta del índice de la raíz.

En este proceso se distinguen tres casos, que serán materia de estudio de los tres siguientes temas.

Caso I

Racionalización del tipo:    

Se multiplica el numerador y el denominador por 

Racionalizar la siguiente expresión algebraica:

Se multiplica el numerador y el denominador por 

Racionalizar la siguiente expresión algebraica:

Se multiplica el numerador y el denominador por 

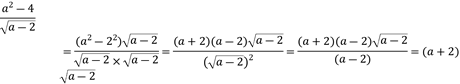
Caso II

Racionalización del tipo: 

Se multiplica numerador y denominador por    

Racionalizar la siguiente expresión algebraica:

Se multiplica numerador y denominador por 

Racionalizar la siguiente expresión algebraica:

Se multiplica numerador y denominador por 

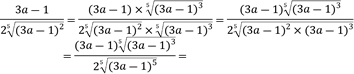
Caso III

Racionalización del tipo:     en general cuando el denominador sea un binomio con al menos un radical.

Se multiplica el numerador y denominador por el conjugado^[25] del denominador, para abordar este tipo en particular de racionalización de expresiones algebraicas; se debe tener presente que el producto de dos binomios conjugados corresponde a una diferencia de cuadrados (tal como ya se mencionó) presentan dos casos:

a) Cuando el denominador es un binomio cuyos términos es la suma de dos radicales , se multiplica numerador y denominador por el conjugado del denominador y se resuelve de acuerdo a lo siguiente:

Racionalizar la siguiente expresión algebraica.

Se multiplica numerador y denominador por el conjugado del denominador   

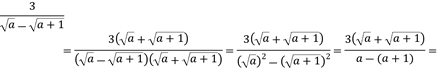
b) Cuando el denominador es un binomio aditivo y uno de los términos carece de radical    , se multiplica numerador y denominador por el conjugado del denominador     y se resuelve de acuerdo a lo siguiente:

Racionalizar la siguiente expresión algebraica:

Se multiplica numerador y denominador por el conjugado del denominador .

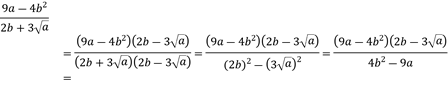
Este proceso de racionalización es también extensivo al campo de los números reales.

2.6 Problemario

1. Traducir a lenguaje algebraico los siguientes enunciados:

1.1. El doble de un número

1.2. La tercera parte del cuádruple de un número

1.3. El producto de la suma por la diferencia de dos números

1.4. La suma de tres números consecutivos

2. Traducir del lenguaje algebraico al lenguaje ordinario las siguientes expresiones algebraicas.

2.1.

2.2.

2.3.

2.4. x-5

3. Calcula el valor numérico de las siguientes expresiones para los valores dados a continuación:  a=1, b=2, c=3, d=4

3.1.

3.2. c(a+b)

3.3.

3.4.

4. Sumar con

5. Restar de

6. Multiplicar:

6.1. 5x²y⁴ por -4x³y²z³

6.2.   por 

6.3.   por 

6.4. por

7. Resolver las siguientes divisiones

7.1.

7.2.

7.3.   entre 

7.4.   entre 

8. Por división sintética dividir entre x+1

9. Resolver las siguientes operaciones:

9.1.

9.2.

9.3.

10. Desarrolla los siguientes productos notables:

10.1. (5+x)(5-x)

10.2. (3x+2)(3x+2)

10.3. (2x-y)³

10.4. (x+y)⁵

11. Factorizar:

11.1.

11.2. 5x(a+b)-4y(a+b)

11.3.

11.4. 4x²-100

11.5.

11.6.

11.7.

11.8.

11.9.

11.10.

11.11.

12. Racionaliza las siguientes expresiones:

12.1.

12.2.

12.3.

2.7 Soluciones del problemario

1.1. 2x

1.2.

1.3. (a+b)(a-b)

1.4. x+(x+1)+(x+2)

2.1. La mitad de la diferencia de dos números

2.2. El triple de la suma de dos números

2.3. El doble del cuadrado de un número

2.4. Un número disminuido en 5

3.1.

3.2. 9

3.3. 7

3.4. 7

4.

5.

6.1.

6.2.

6.3.

6.4.

7.1.

7.2.

7.3. Cociente: x+4, residuo:2

7.4. Cociente: , residuo 3

8. 2x³+x

9.1.

9.2. 1

9.3.

10.1.

10.2.

10.3.

10.4.

11.1.

11.2.

11.3.

11.4.

11.5.

11.6.

11.7.

11.8.

11.9.

11.10.

11.11.

12.1.

12.2.

12.3.

2.8 Conclusiones^[26]

En este apartado de álgebra vimos la notación científica, misma que aplican profesionistas como los astrónomos, biólogos, físicos, químicos, matemáticos y otros pues, su empleo se relaciona con unidades  macroscópicas y microscópicas, de las cuales aprendiste sus múltiplos y submúltiplos.

En una conferencia impartida en 1959 por uno de los grandes físicos del siglo pasado, el maravilloso teórico y divulgador Richard Feynman,  predijo que había un montón de espacio al fondo (el título original de la conferencia fue: There’splenty of room at thebottom) y auguraba una gran cantidad de nuevos descubrimientos si se pudieran fabricar materiales de dimensiones atómicas o moleculares. Hubo que esperar varios años para que el avance en las técnicas experimentales, culminado en los años 80 con la aparición de la Microscopía Túnel de Barrido (STM) o de Fuerza Atómica (AFM), hiciera posible primero observar los materiales a escala atómica y, después, manipular átomos individuales. Con respecto a que es la Nanotecnología, empecemos por aclarar el significado del prefijo nano: este hace referencia a la milmillonésima parte de un metro (o de cualquier otra unidad de medida). Para hacernos una idea de a qué escala nos referimos, piensa que un átomo es la quinta parte de esa medida, es decir, cinco átomos puestos en línea suman un nanómetro. Bien, pues todos los materiales, dispositivos, instrumental, etc., que entren en esa escala, desde 5 a 50 o 100 átomos, es lo que llamamos Nanotecnología. Como podrás darte cuenta en todo esto se aplica el álgebra. Es de suma importancia que lo aprendido en este tema lo relaciones y lo pongas a funcionar con los efectos cotidianos, y es en el siguiente apartado donde se te proporcionará una serie de herramientas para tal efecto. 

Referencias

[1] Eliseo Martínez H., Héctor Varela V.,  Proyecto "Web en apoyo al estudio de las matemáticas", Universidad de Antofagasta. Introducción al álgebra para los estudiantes de primero medio.

[2] Gal, O., & Chen-Morris, R. (2005). Metaphysical images and mathematical practices: The archaeology of the inverse square law part I.

[3] Gal, O., & Chen-Morris, R. (2005). The archaeology of the inverse square law:(1) Metaphysical images and mathematical practices. History of science, 43(4), 391-414.

[4] Heilbron, J. L. (1982). Elements of early modern physics. Univ of California Press.

[5] Whiteside, D. T. (1982). Newton the mathematician. In Contemporary Newtonian Research (pp. 109-127). Springer.

[6] Guía de estudio para padres y alumnos. Matemáticas: Aplicaciones y conceptos curso 3. Glencoe/McGraw-Hill.

[7] Álvarez J. Rafael & Mejía D. Francisco (2006). Factorización. Universidad de Medellin.

[8] Universidad Michoacana de San Nicolás de Hidalgo. Coordinación de Innovación Educativa (CIE).

[9] Álvarez J. Rafael &Mejía D. Francisco (2006). Factorización. Universidad de Medellín.

[10] Las expresiones algebraicas.  Recuperado: 01 de Agosto del 2011.

http://www.oocities.org/mx/amiga_miraba/articulos/expresiones.html

[11] Universidad Michoacana de San Nicolás de Hidalgo. Coordinación de Innovación Educativa (CIE).

[12] Consultar tópico 4.8  Factorización de expresiones algebraicas de este tema.

[13] Consultar tópico 4.4.5. Simplificación de expresiones algebraicas racionales de este tema.

[14] Ver tópico 4.8.  Factorización de expresiones algebraicas de este capítulo.

[15] Algebra elemental. Dr. Aurelio Baldor. Cultural Mexicana S.A. México? (1972).

[16] Wentworth, George; y Smith, David Eugene (1917). Ginn & Co. (ed.). Elementos de Algebra, 2a edición.

[17] Universidad Michoacana de San Nicolás de Hidalgo. Coordinación de Innovación Educativa (CIE).

[18] Kurt Gieck (1981). Manual de fórmulas técnicas. Representaciones y servicios de ingeniería S.A. MEXICO

[19] Álvarez J. Rafael &Mejía D. Francisco (2006). Factorización. Universidad de Medellín.

[20] Algebra elemental. Dr. Aurelio Baldor. Cultural Mexicana S.A. México (1972).

[21] Ver tópico 5.2.2  Variable, variable independiente y variable dependiente del capítulo 5.

[22] Aula fácil.com: CUATRINOMIO CUBO PERFECTO DE BINOMIOS.

http://www.aulafacil.com/algebra/curso/Lecc-32.htm

[23] Aula fácil.com: CUATRINOMIO CUBO PERFECTO DE BINOMIOS. Recuperado : 12 Jul del 2011

http://www.aulafacil.com/algebra/curso/Lecc-32.htm

[24] Vitutor (2010) Racionalización de radicales. España. Archivo de blog.

[25] Tema ya revisado en el tópico 4.7.2. Binomios conjugados de este capítulo.

[26] INSTITUTO POLITÉCNICO NACIONAL. CECyT “MIGUEL BERNARD PERALES”.ACADEMIA DE MATEMÁTICAS.GUIA DE ALGEBRA PRIMER DEPARTAMENTAL. .