Texto académico
Autores
Eduardo Ochoa Hernández
Nicolás Zamudio Hernández
Gladys Juárez Cisneros
Filho Enrique Borjas García
Lizbeth Guadalupe Villalon Magallan
Pedro Gallegos Facio
Gerardo Sánchez Fernández
Rogelio Ochoa Barragán

Unidad 1. Aritmética
1. ¿Qué es un número?
Al igual que las obras literarias, las obras matemáticas nos ayudan a expandir nuestro círculo de empatía, liberándonos de la tiranía de un único punto de vista. Los números, debidamente considerados, nos hacen mejores personas. Por ejemplo, al pensar en los muchos puntos que infinitamente pueden dividir el espacio de nuestro corazón. Utilizamos a los números para dar sentido a nuestra realidad. Nos dicen cuantas categorías de cosas hay en nuestro alrededor. La hora en que veremos a alguien para conversar en un café. La edad que tendremos al egresar de la universidad. La cantidad de sal para cocinar unos chilaquiles. La distancia a la que está nuestra casa de la escuela. La velocidad de nuestra bicicleta. El número de hermanos que tenemos. Lo pequeño que somos comparados con las estrellas en el cielo. Nos ayudan a entender como invertimos nuestro tiempo, dinero y vida. En fin, los números los hay enteros, decimales, reales, imaginarios, irracionales, racionales, negativos, positivos, primos, y ellos están dentro de la toma de decisiones (probabilidad); en la medida de las dimensiones del espacio (geometría); en la cuenta de elementos de categorías (conjuntos); para identificar la unidad en las capas de la realidad (mónada); para realizar cálculos (lógica).
El rechazo de Aristóteles al pensamiento matemático fue antitético a la filosofía de su maestro Platón. Por otro lado, Pitágoras estudio aritmética, geometría, música y astronomía y postuló que los números enteros eran cruciales, por su notable capacidad para explicar, por ejemplo, los armónicos musicales y las propiedades de los objetos geométricos. La escuela pitagórica aseguro que los números enteros eran esenciales para una comprensión fundamental de la forma en que el universo está diseñado. Platón considero a las matemáticas fundamentales para hacer filosofía y que la geometría llevaría a la comprensión del mundo. Sin embargo, es Euclides quien introduce nuevos estándares de rigor al pensamiento matemático[1]. El libro de Euclides “Elementos” se convirtió en el texto más influyente durante siglos, Einstein comento al respecto: “si Euclides no encendió tu entusiasmo en la juventud, entonces no naciste para ser científico[2]”. La idea de las regularidades en el comportamiento de los objetos que los humanos observamos en la Tierra, se pensó desde Arquímedes, eran descritas por leyes matemáticas. Este fue el primer paso de hacer trascender los sentidos humanos, es decir, al desplegar el poder de la razón imaginativa, con la mirada levantada a los objetos en el cielo.
Para comprender las ideas matemáticas, la biología y su ciencia cognitiva están interesadas en dar respuestas en el cómo los individuos entienden, aumentan su rendimiento y por qué algunos encuentran tantas dificultades en su aprendizaje matemático. La neurociencia, la genética y la psicología están conjuntando esfuerzos en el estudio de la subitización[3]. A la competencia matemática que se presenta como un desarrollo temprano de la habilidad numérica se le llama subitización y conteo. La primera, refiere a la numeración de elementos entre 1 y 4 dado por reconocimiento de patrones. El conteo además de hacerlo uno a uno, asigna símbolos dentro de un sistema numérico[4].
Subitización es un término científico que refiere a la habilidad de identificar y numerar objetos, sin error, rápidamente y exacto. Se cree que es la base del mismo mecanismo del conteo[5]. La acción de numerar es la habilidad de crear el valor total de un conjunto de elementos y la habilidad innata de numerar una cantidad pequeña de 1 a 4 en 250 milisegundos sin contar y libre de errores; a esto, los biólogos desde 1941 le nombraron subitización[6]. Subitización no es estimar una cantidad, sino un conocimiento de un patrón intuitivo[7], es preverbal, una cantidad concreta visual espacial. El conteo y la subitización solo pueden darse cuando se une la información visual de los objetos y se localiza a la unidad dentro de ellos[8].
La memoria de trabajo es un sistema necesario para acumular actividades complejas de conteo de grandes números[9], se especula que allí existe un buffer de acumulación secuencial, conformado por los mecanismos de focalizar la unidad (mónada) dentro de un conjunto de elementos, la capacidad de subitizar y la visión espacial, todos ellos juegan a favor de desarrollar mayor complejidad en los rangos de una cuenta, pero son procesos diferentes[10]. El conteo es un proceso articulado en el buffer de manera serial y de acumulación simultánea, la subitización es más exacta, rápida y permite en pequeños rangos ganar exactitud en modo de tramos de numeración no simbólica. El conteo es ya un proceso simbólico con un rol de intención de cálculo de rangos mayores a 4 elementos y que permite llegar a grandes numeraciones. Además diferenciemos, el conteo es una estimación, un proceso de probabilidad de cálculo por subitización, el cual es inexacto y con errores siempre presentes en sus determinaciones.
Un número implica para su comprensión ideas de las disciplinas pedagógicas neuronales y matemáticas en procesos subyacentes de aprendizaje, es la cognición matemática empleada por los individuos para reconocer que en la realidad hay patrones numéricos. Se estima que el 24% de los adultos tienen dificultades para realizar cálculos de numeración equivalentes a niveles inferiores a los establecidos en niños de 8 años, se refiere a cálculos de conteos, fraccionarios, porcentajes y manejo de decimales[11]. Los científicos creen que el aprendizaje desde las capas subyacentes de la base biológica de los axiomas, permite más eficazmente aprender a identificar las ideas matemáticas que son cimientos y en consecuencia, mejora la abstracción del pensamiento matemático en todos aquellos que batallan con este tipo de conocimiento[12].
El rendimiento matemático está implicado con la aplicación formal de sistemas de representación simbólica con bajo contacto intuitivo de los axiomas de unidad, espacio geométrico, probabilidad, lógica y categorización. Los sistemas simbólicos representan ideas matemáticas que los estudiantes deben relacionar con la vida cotidiana justo antes de las estructuras formales simbólicas, esta pedagogía de las matemáticas es el paradigma proceptual-simbólico[13].
¿Qué es realmente un número? ¿Existen números como objetos abstractos independientes del lenguaje humano? ¿Son objetos lógicos construidos dentro de un sistema axiomático dado como lo sugieren los formalistas? O son simplemente etiquetas generadas por un sistema numérico para referir a tipos de cantidades o conjuntos. Otros, los más recientes en la escena científica, refieren a número como el resultado de habilidades innatas de la cognición matemática[14]. La cognición matemática ha descubierto procesos implicados en la comprensión de las ideas matemáticas y la forma de representación numérica en la aritmética. Es claro que los niños lactantes son capaces de procesar información numérica antes de aprender su representación simbólica. Este proceso innato de numerar y reconocer a la unidad dentro de las capas subyacentes de la realidad, permite a los niños desarrollar en adelante habilidades formales del pensamiento matemático. La subitización ha demostrado que la actividad de numerar está antes de que se conecten la palabra con número y símbolo dentro de un sistema numérico. Una vez que se aprende el sistema generador de números, los niños empiezan a usarlos en operaciones aritméticas.
La verdadera competencia aritmética desarrolla la idea de operador numérico de adición, sustracción, multiplicación y división; pero se requiere el conocimiento básico de número dentro de un entrenamiento formal del sistema simbólico numérico. Comprender lo que es un operador, nos ayuda a relacionar lo que es una operación aritmética al elegir las estrategias adecuadas para su cálculo. La memoria de trabajo se expande y la atención racional se agudiza para reflexionar la habilidad intelectual de numerar, estimar y el conteo de numerales grandes. Numeral lo referimos a la representación simbólica de número, pero en adelante unificamos la idea en simplemente número, como dos dimensiones, una refiere a patrones subitizar de cantidad y otra a un sistema numérico simbólico formal.
Los números racionales requieren que los niños vayan más allá de la lista de una cuenta de indexar símbolos con cantidades y en referencia profunda a la idea de mónada. Resultan estos números desafiantes para muchos adultos que dentro de las universidades reflejan una baja habilidad cognitiva para su manejo en operaciones aritméticas con racionales. Es necesario que las representaciones simbólicas de números, operadores y signos sean reconocidos desde las ideas intuitivas justo antes de mayores abstracciones simbólicas. Lo proceptual refiere a un aprendizaje que valora como condición inicial, la habilidad de reconocer el significado matemático encapsulado en los símbolos. El pensamiento matemático es habilidad de comprensión (saber por qué: proceptual) y habilidad procedimental (saber cómo hacerlo: sistema simbólico formal).
A los matemáticos les tomó mucho tiempo llegar a preguntarse cuál fue la respuesta y mucho más tiempo para encontrar un número. El primer paso fue caracterizar a los números naturales. Resultó que su rasgo definitorio más importante no fue la noción de cantidad o su aritmética dentro del concepto de álgebra. Sino la prueba por inducción, por ser una mirada más profunda en su sustancia.
Proposición: La suma de los primeros números n naturales es:
![]()
Demostración: Esto es verdadero trivial para n=1. Si bien es cierto
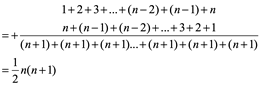
Es decir, dos series infinitas una creciente y otra decreciente las sumamos, luego factorizamos (n+1) y dividimos entre dos, y encontramos la suma total de los números naturales.
Muchos consideran este tipo de demostración como un argumento de prueba de verdad, se establece el estado de la proposición como verdadero. El único problema con esta forma de pensar es que llegar a valores grandes de n requiere de un gran número de aplicaciones de pasos en general. Nunca podremos cubrir todos los números naturales en un infinito de deducciones si procedemos un caso a la vez. Pero una demostración, por definición, se compone de un número finito de líneas de cláusulas hipotéticas deductivas sobre el universo de posibilidades.
La salida a este dilema es eliminar la parte de y así sucesivamente de pruebas por casos repetitivos, de una demostración. Demostrar por inducción entonces es hacer encajar un extenso número de casos (proposiciones) en un tipo de prueba como y así sucesivamente. Un número por deducción e inducción apunta directamente a la definición de número natural.
A los números verbales los llamamos simplemente números y a los escritos numerales. Al referirnos a las cantidades abstractas descritas por los números, nosotros utilizamos símbolos como 1,2,3,4,5,6…, y así sucesivamente. Investigadores lingüistas, antropólogos, psicólogos, biólogos y otros, están creando una nueva historia para los números. Algunos son partidarios de considerar a los números como conceptos que no vienen a las personas de manera innata o natural. Es decir, así como la escritura y la lectura alfabética no son naturales, sino de creación cultural. Los números están ausentes de algunas poblaciones del mundo. La noción de contar es parte del perfil de nuestra especie, dada por un acumulador cerebral para reconocer el paso del tiempo, pero para la noción de número, para esta última es necesario ser educado. El número o numeral, aquí lo referimos indistinto mientras no especifiquemos lo contrario. El número es uno de los inventos claves en el curso de nuestra civilización, vive como una especie de piedra pedernal que encendió la línea de tiempo humana cuando se percibe al universo entero como una estructura de números.
Tal vez la mejor manera de conocer este invento llamado número, es partir de reconocer en nuestro cerebro una habilidad sustancial, la de registrar el paso del tiempo. Pero tal vez, contar el tiempo desarrolló que apreciáramos patrones repetitivos de los ciclos de las estaciones. Es evidente que nuestra percepción del tiempo pasa por el papel de número en nuestra reflexión. ¿Qué significa percibir o sentir el tiempo? El tiempo es percibido en términos culturales, una especie de consenso de la experiencia cultural de una sociedad. A menudo los humanos de cualquier cultura reconocen el paso del tiempo, en términos de algo que pasó. El tiempo no es un parámetro de movilidad lento o rápido, el tiempo no se mueve realmente, no pasamos a través de él. Los científicos cognitivos establecieron hace tiempo que los seres humanos tienen una tendencia generalizada a utilizar especialmente cosas concretas, como los objetos materiales. Es decir, asumimos al tiempo como algo objetivo y parte del mundo material de nuestra vida. Así, sí nuestra vida cambia, es hablar de movimiento usando el paso por momentos de la existencia y siendo incapaces de volver en la dirección presente-pasado. Es a través de nuestra conciencia cerebral que enfrentamos el futuro como pasado en potencia a través de nuestro acumulador neuronal que registra una porción progresiva de cantidades. El habla humana es evidencia de las expresiones del tiempo, de cómo lo sentimos, por ello podemos hablar en presente, pasado y futuro, incluso desaparecer al tiempo. La mayoría de los humanos, percibimos el paso del tiempo en la manera en que contamos, escribimos y leemos[15]. La música podemos verla como otro sistema artificial que el hombre inventó, reconociendo en ella las sensaciones del tiempo.
En la base espacial numérica, podemos reconocer las formas flexibles de pensamiento evidente, en el cómo consideramos cantidades naturales en una línea de tiempo. Es decir, consideramos las cantidades a la izquierda (pasado) y la derecha (futuro) y el presente metafóricamente instante de existencia. Así la cultura creó calendarios, barras de progreso en descarga de archivos “PDF”, líneas de tiempo en los libros de historia y así sucesivamente. Y hay sólida evidencia científica que sugiere que las prácticas simbólicas por defecto impactan en el cómo percibimos al tiempo. Los científicos observan que al pedir a un grupo de personas que organicen un conjunto de fotografías, tienden siempre a colocarlas de izquierda a derecha en el sentido temporal que ellas infieren[16].
Estas pruebas reflejan un punto importante, apostamos a que el tiempo es una práctica cultural y lingüística, como resultado del acumulador que registra el paso del tiempo. Y aquí es donde nace la historia del número, como un símbolo que afecta todas las nociones de nuestra existencia. Los números naturales poseen la dirección del tiempo percibido, son los números claros obtenidos del pensamiento del movimiento del tiempo. Si pensamos al tiempo como algo que fluye, moviéndose a lo largo de la línea de tiempo frente a nosotros, su paso es contable, divisible y misterioso en cuanto a su límite. Piense en barras de progreso de descargas de archivos informáticos, la realidad, es que hay eventos que requieren ciertos procesos que consumen tiempo antes de que se manifieste un cambio significativo, los números naturales quizá fueron estos cambios significativos, donde la unidad es el mínimo cambio detectable al paso del tiempo. Esta conceptualización centrada en el número como paso de tiempo podría decirse que rige nuestra vida.
¿Qué hora es al momento que realiza esta lectura? Para nosotros, son las 13:51 al momento en que escribimos estas palabras en el occidente mexicano. Puesto que en este momento del día estoy en mi oficina, en mi escritorio, y no en mi casa. Qué significa esto, 13 horas y 51 minutos contados desde la media noche, en realidad nuestra experiencia mental es numérica. Son los números resultado de crear un medio para cuantificar nuestra existencia, dividir metafóricamente el paso del tiempo en unidades manejables para planear nuestra vida. Son un indicador del hecho de que los seres humanos en algún momento decidieron cuantificar momentos de tiempo de la experiencia. El tiempo puede ser real, existe además de nuestra experiencia, pero el número es una invención para relacionarnos con el mundo. De hecho, cuando respondemos sobre ¿qué hora es?, contestamos lingüísticamente con una tradición cultural que adoptó un sistema antiguo de numeración.
Al considerar la división de cada una de las rotaciones de la tierra, cada día, en 24 horas. ¿Por qué se dividió de este modo? No hay ninguna motivación astronómica en esta división. Después de todo, en teoría podría ser dividida un día sobre cualquier número. Fueron los egipcios los que para sus relojes de hace 3 mil años dividieron la luz del día en doce partes iguales. De esta división de la luz en el transcurso del día nace una tradición cultural apropiada para su sentido de la existencia. Así de esta manera, la unidad de tiempo para los relojes, fue el número 12, así la base numérica de la sensación del paso del tiempo para la luz del día fue duodecimal. Los sistemas de numeración, hay muchos de ellos, basados en muchas cosas diferentes. Sin embargo, para nosotros hoy, el sistema duodecimal está muy arraigado para contar el paso del tiempo, impone una cierta perspectiva en nuestro día a día. Nuestra vida cotidiana está gobernada por números para las horas, minutos y segundos. Pero en realidad el tiempo no ocurre en estas u otras unidades discretas. La segmentación del tiempo es contable en unidades producto de la mente humana[17].
Contar el tiempo, es una necesidad que impulsó al hombre a crear la noción de número natural, sistema de numeración y gobierna las conductas sociales de nuestra civilización. Inventar al número como depositario de cantidad, pasó desde luego por la noción cultural de unidad de cantidad o mónadas como Leibniz las nombró. Esta idea abstracta de unidad, es el antecedente más relevante de nuestra especie para dar orden temporal a nuestro plan de vida. La unidad, es el concepto esencial e íntimo vinculado a la historia de los números.
El registro fósil sugiere que los homínidos, fueron capaces de registrar cantidades bajo el concepto de unidad. Los humanos modernos tenemos unos 100 mil años que surgimos, debemos aceptar que no fuimos nosotros los que descubrimos la unidad, pero sí fuimos nosotros los que con esta abstracción desarrollamos el invento de número. En el cruce temporal entre homínidos y humanos, allí está el origen del número[18]. Quizá una forma razonable, es que los Homo sapiens en su competencia por sobrevivir, intentaron descifrar los primeros registros rupestres de las cuevas de los homínidos. Así aprendimos la idea de unidad, como abstracción de algo necesario para establecer una cuenta de registro. La unidad fueron semillas, patos, caballos, hombres…, a menudo la unidad fue algo útil para que el registro fuera una memoria útil. Este cambio cognitivo es evidente, en la fabricación de tecnología de puntas de flecha, herramientas de hueso, quizá la teoría de supremacía del Homo sapiens sobre sus parientes más cercanos, es que la abstracción de la unidad a número en una cuenta natural, fue determinante para tomar ventaja tecnológica[19].
De esta historia, podemos aprender, que las sociedades con mayor dominio matemático, son las que más poder acumulan y se hacen valer en forma de dominio tecnológico. Planear una guerra, es hacer uso del más sofisticado conocimiento matemático, solo baste ver el resultado del proyecto “Enigma” que decidió el rumbo de la segunda guerra mundial. Alan Turing fue el principal responsable de descifrar Enigma, el código secreto utilizado por el ejército alemán en la Segunda Guerra Mundial, contribuyendo con ello a acortar la guerra. Inventó una máquina, que permitía descifrar mensajes de Enigma de forma masiva, así nació la guerra cibernética, impulsada por avances matemáticos en materia de cifrado y codificación de códigos. Quizá lo que los Homo sapiens lograron, fue descifrar la noción de unidad de los homínidos, y tomar ventaja similar a lo hecho por Alan Turing para ganar la guerra.
La historia del número, es la misma explicación que nos hace lingüísticos por actos de invención y creación de sistemas alfabéticos y numéricos. Esta creación, es decir, invenciones no naturales, nos dieron la habilidad de comunicar, cooperar y organizar colectivamente el poder del conocimiento, transmitiendo por símbolos mensajes al futuro, haciendo portable la información y creando un arte de números y letras, que a la postre desarrollaron la civilización de manera espectacular[20]. Pero tenga presente, que la noción de número a partir de la idea de unidad, creó las bases de todo el sistema de numeración moderno.
Como conclusión parcial, un número es un símbolo dentro de un sistema numérico construido bajo las nociones de registro del tiempo y unidad (cantidad), donde es resultado de una tradición cultural que ha elegido una base numérica como patrón representativo de la existencia humana. El número está como noción innata en nuestra biología.
1.2 Contar números
Desde tiempos tempranos del hombre en la tierra, surge la necesidad de contar, hacer un registro de animales, frutas, guerreros y muchas cosas más. Para ello emplearon pilas de piedras, marcas en huesos, palos de madera y dedos de las manos que al paso del tiempo se convirtieron en la base del sistema numérico de base 10. Los Mayas emplearon la base 20, y en Mesopotamia la base 60.
La unidad como abstracción matemática en todas las culturas fue desarrollada. La unidad para la noción de un símbolo que asocia cantidad dentro de un sistema numeral fue fundamental, así el número es la base de contar. En nuestro familiar sistema decimal, basado en el número 10, se escriben los números posicionándose en columnas separadas para las unidades (1), diez (10), cientos (100), miles (1000)…, a medida que avanzamos de derecha a izquierda. El conjunto de símbolos de este sistema son 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Este sistema de valor refleja las cantidades asociadas colocando cada símbolo en su columna, multiplicando por su valor asociado a cada columna y sumando podemos determinar la cantidad asociada en base 10. Por ejemplo el número 579:
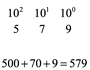
![]()
El valor de cada número de una cifra depende de su posición.
Para un sistema posicional numérico de base 5, el conjunto de símbolos son 0,1,2,3,4, ¿qué cantidad base 10 representa el número 2341 base 5?
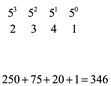
Resolviendo en Wolfram Alpha https://www.wolframalpha.com
 11.20.09.png)
![]()
Para un sistema numérico posicional de base 16, el conjunto de símbolos es 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F, ¿qué cantidad base 10 representa el número E3FD base 16? Donde A=10, B=11, C=12, D=13, E=14, F=15 en cantidad.
 11.14.26.png)
![]()
Podemos inventarnos cualquier sistema numérico posicional, por ejemplo uno de base 7, su conjunto de símbolos sería 0,1,2,3,4,5,6, ¿qué cantidad base 10 representa el número 4351 base 7?
 11.26.19.png)
![]()
Podemos inventar un sistema numérico posicional de base 32, su conjunto de símbolos sería (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V), ¿qué cantidad base 10 representa el sistema 89FMV base 32?
 18.35.19.png)
 18.35.25.png)
Para un sistema numérico posicional de base 2, el conjunto de símbolos es (0,1), ¿qué cantidad representa el número 10101101 base 2, en cantidad base 10?
 18.49.07.png)
Con los sistemas numéricos podemos contar toda clase de objetos de la realidad. Pero, si no hubiera nada allí, no habría necesidad de contar, simplemente introducimos el número cero o incluso parece menos necesario utilizar números negativos, por ejemplo, la expresión - 8 chivos para los hombres antiguos hubiera parecido sin sentido.
Para ver de un modo natural el concepto de cero y los números negativos en nuestra época, podemos imaginar 0ºC, -5ºC. Pero los conceptos de cero y números negativos llevaron miles de años para emerger, aunque en nuestro tiempo parecen muy naturales. Las primeras apariciones de los números cero y los negativos se presentaron probablemente en el comercio. Las ganancias fueron registradas como números positivos, las deudas con números negativos y cero el equilibrio.
Hace algunos años se desarrollaba una amplia discusión en cuanto a si el nuevo milenio debe comenzar en el año 2000 (que lo hizo) o en el 2001 (desde el siglo XX comenzó en el 1901). El problema surgió porque no había ningún año 0. Los términos “antes de Cristo AC” y “después de Cristo DC”, fueron introducidos en el año 531 por Dionysus Exiguus, pero él no los podía establecer como año 0, porque para ese año no se había introducido año 1 AC inmediatamente después del año 1 DC. Un sistema más natural fue introducido en 1740 por el astrónomo Jacques Cassini, él elige seleccionar como año 0 justo el año de nacimiento de Cristo y manteniendo los años AC y DC justo uno antes y uno después de 1, por lo tanto el milenio sin duda inició en el año 2000.
Antes de continuar, debemos distinguir claramente entre cero y nada. Cero es un número como cualquier otro número, solo que este representa indeterminación de cantidad, si dividimos la unidad entre infinito, es decir ![]() , es la incertidumbre de aproximarnos a la nada. Mientras la nada significa la ausencia de cualquier cosa, incluyendo cantidad en sentido abstracto.
, es la incertidumbre de aproximarnos a la nada. Mientras la nada significa la ausencia de cualquier cosa, incluyendo cantidad en sentido abstracto.
Desde este punto, los números naturales son la base de un sistema numérico y la cuenta infinita dentro de este sistema son también números naturales, dado que son cuentas de unidad en unidad como proceso natural. La idea de número se aplica con los conceptos de cero y negativos, generando a la familia de números enteros. Los enteros son los números naturales positivos, los negativos y cero. Tenga en cuenta que 0 es identidad aditiva para nuestros sistemas de numeración, es decir, añadiendo cero a cualquier número no le produce cambio, si x es una variable que recibe números, entonces sí sumamos cero, x+0=x, para todo x. Así como 1 es el elemento neutro bajo la multiplicación (x)x1=0.
Ni Griegos, ni Egipcios utilizaron al cero, en su estilo geométrico de ver a la aritmética, el número a menudo es representado por longitudes de líneas, así que 0 o longitud cero habría sido difícil de imaginar. Pero los mesopotámicos con su sistema numérico de base 60, aún sin dejar huecos para indicar ninguna entrada de números en esa posición, en el cero se espera que el valor previsto en dicha posición sea un comodín para marcar el salto del final al principio de la base numérica, en tal caso lo empleamos hoy en día. Pero ese cero no tiene concepto para emplearse al modo de cálculo, el cero para el cálculo lo introducen los Mayas . Es decir, en términos modernos, una aproximación a la nada de manera infinitesimal en base 10.
El cero Maya nos dice para la geometría, que un infinitesimal ![]() dimensional en el espacio, tiene largo, ancho y alto. Es decir, el cero dentro de un sistema geométrico representa el origen del sistema y es un infinitesimal de tres dimensiones de algo que existe en ese espacio.
dimensional en el espacio, tiene largo, ancho y alto. Es decir, el cero dentro de un sistema geométrico representa el origen del sistema y es un infinitesimal de tres dimensiones de algo que existe en ese espacio.
Los Indios sin embargo, desarrollaron un sistema numérico decimal basado en los números 1 a 9 y más adelante introducen el cero, estos diez dígitos podían representar cualquier número entero, por grande que fuera. Pero el cero indio representó el conjunto vacío, es decir, la nada. Pero en su sistema el cero representó un comodín para la transición de la secuencia de la base numérica.
Desde este momento en adelante el cero podría ser utilizado en la aritmética de números enteros negativos y positivos. Después de haber tratado con la suma, resta y multiplicación en donde el cero, el uno y los negativos mostraron coherencia total en la aritmética, pero con la atención de la división restrictiva de cualquier número entre cero,
0/0=0
a/0=? No está definido, donde a es cualquier entero diferente de cero.
Pudiéramos decir que a/0 es infinito, pero infinito no es un número y no obedece a las reglas de la aritmética, por ejemplo:
![]()
La división sobre cero de un número diferente de cero, no está definido, es una incoherencia dentro de las matemáticas, basta con emplear una computadora y programar en ella una división sobre cero, el código de computadora provocará que el sistema se vuelva inestable.
De los números naturales, pasamos a los números enteros, ahora pasaremos a los números reales que agregan otras dos clases de números. Otros tipos de números surgen de la división, estas fracciones pueden ser racionales o irracionales, en ellos están los números pi y e. Y al conjunto que agrupa a los números naturales, enteros, fraccionarios positivos y negativos se le llama, conjunto de números reales. Pero es hasta que cero es establecido en el cálculo cuando los fraccionarios se desarrollan.
El uso del cero en cálculos aparece en las diferencias, 4 - 5=-1, y la diferencia de 5 -5=0 ajustando el estatus matemático a los negativos y la neutralidad de cero:
1+0=1; 5-0=5; 0+0=0; 0-0=0; 0-4=-4.
A partir de aquí, cero es parte del sistema aritmético. Reservando que no está definida la división de los números entre cero.
Después de haber tratado con la suma, la multiplicación y la resta, se atendieron los números positivos o negativos a/b, donde b es distinto de cero. Mientras 0/0=0 es una definición vacua.
El camino a los números reales se abre después de que tenemos claro que a/a es un número entero, que los hay positivos y negativos y cero. De los fraccionarios podemos deducir que en ellos habitan los números enteros positivos, negativos y el cero. Al romper un número en fracciones nos permite la división del número. Al multiplicar una fracción simplemente multiplicamos denominador por denominador y numerador por numerador de las fracciones:
![]()
Para sumarlos o restarlos, primero colocamos a los fraccionarios con denominador común y luego procedemos a la resolución de una suma modesta.
![]()
Las fracciones ya estaban plenamente establecidas para el momento en que el cero apareció en la escena, particularmente en los problemas de comercio entre sociedades.
1.3 Aritmética
Los apartados anteriores se consideran elementales para la currícula básica de las matemáticas en el mundo. Se enseñan a nivel de educación básica en las escuelas. Aunque todos estos aspectos del pensamiento matemático son considerados elementales, no hay un límite claro entre las matemáticas elementales y avanzadas. Podemos rescatar del contexto anterior, conceptos como infinito, abstracción, demostración, objeto matemático, objetividad, existencia y base axiomática en las matemáticas, que son inseparables para comprender matemáticas.
En casi todo el mundo se refiere a la Aritmética como el dominio humilde de la adición, sustracción, multiplicación y división de números enteros y fracciones. Se comienza con la noción de números naturales en la primaria y se concluye con el entrenamiento de la misma en dispositivos electrónicos (calculadora). Pero desde Euclides se ha cultivado la teoría de los números, resolución de ecuaciones con enteros, el algoritmo de la división (cómo encontrar el máximo común divisor de dos números enteros positivos) y factorizar en números primos, como parte de la aritmética.
Esta álgebra de números (aritmética) nace con la búsqueda de soluciones enteras positivas a ecuaciones como estas:
![]()
Sorprendentemente ayudan a introducir números de la forma:
![]()
Donde a, b son enteros ordinarios, y se pretende que estos nuevos números se comporten como enteros ordinarios. La previsión es realmente justificable, dado que nos permite desarrollar y explorar la teoría de los números primos.
Para esta fracción 2727931/2336107, ¿cómo saber si está en su forma reducida? Es decir, que ningún divisor común al numerador y al denominador existe. Para responder esta pregunta, tenemos que encontrar el máximo común divisor de 2727931 y 2336107, que parece difícil. Incluso encontrar los divisores de 2727931 parece difícil, y de hecho no hay ningún buen método establecido para números muy grandes. Es destacable, que puede ser más difícil encontrar los divisores comunes de dos números, que encontrar el divisor particular de cada uno de ellos. Por ejemplo, independientemente sabemos que el máximo común divisor de 30000033 y 30000032 es 1, sin saber los divisores de cualquiera de estos números. ¿Por qué? Pues bien, si d es un divisor común de 30000033 y 30000032 tenemos:
30000032=dp
30000033=dq
Donde p y q son enteros positivos. Y por lo tanto:
30000033- 30000032= d(q - p)
Donde d también divide a la diferencia de 30000032 y 30000033, que es 1. Pero el entero positivo solo se divide sobre 1, entonces d=1. Más generalmente, si d es un divisor común de dos números a y b, entonces d también divide a - b. En particular el máximo común divisor de a y b es un divisor de a - b.
Este simple hecho es la base de un algoritmo eficiente para encontrar el máximo común divisor. Se llama algoritmo euclidiano, escrito por Euclides en su libro Elements hace más de 2000 años. Formalmente uno calcula una secuencia de pares de números de la siguiente manera. Comenzando con un determinado par a, b; donde a>b, cada nuevo par consiste en el miembro más pequeño de la pareja anterior y la diferencia de la anterior pareja. El algoritmo termina cuando un par de números son iguales o cuando la menor diferencia comienza de nuevo a crecer, cada uno de ellos es el máximo común divisor de a y b. Por ejemplo, si fuera a=76 y b=64:
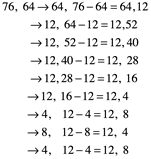
gcd(76,64)=gcd(64,12)=gcd(52,12)=gcd(40,12)=gcd(28,12)=gcd(16,12)=
gcd(12,4)=4
La principal razón por la que el algoritmo euclidiano funciona es porque el máximo común divisor de a y b también es divisor de a - b. Si se denota como gcd, entonces gcd(a,b)=MCD(b, a-b) para a=13 y b=8:
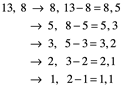
gcd(13,8)=gcd(8,5)=gcd(5,3)=gcd(3,2)=gcd(2,1)=gcd(1,1)=1
Tome en cuenta que, cuando empezamos con los números de Fibonacci consecutivos 13 y 8, la resta son todos los anteriores números de Fibonacci, y todos terminan inevitablemente en el número 1. Es el mismo con cualquier par de números consecutivos de Fibonacci, por lo que MCD de cualquier par de estos es 1. Por ejemplo, a=2584 y b=1597:

Otra razón importante, es que el algoritmo produce continuamente números más pequeños y por lo tanto, termina con números iguales porque enteros positivos no pueden disminuir para siempre. Este principio asegura que no encontraremos ninguna pendiente de descenso infinita, es obvio, sin embargo, es prueba por inducción y base de la teoría de números.
Propiedad de la división. Para cualquier número natural a y b diferentes de cero, son números naturales q y r (cociente y resto) tal que:
![]()
donde
![]() .
.
La ventaja de la división con el resto es que generalmente es mucho más rápido, que restas repetidas. Es lo suficientemente más rápido para encontrar el MCD de números con miles de dígitos. Por ejemplo, a=93164 y b=5826:
Paso 1: 93164 dividido entre 5826 es 15 y sobran 5774
Paso 2: 5826 dividido entre 5774 es 1 y sobran 52
Paso 3: 5774 dividido entre 52 es 111 y sobran 2
Paso 4: 52 dividido entre 2 es 26 y sobran cero
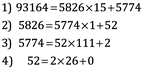
Así que gcd(93164, 5826)=2
El algoritmo euclidiano, como cualquier algoritmo produce una secuencia de eventos. Cada evento depende de una manera sencilla del evento anterior, pero uno no capta toda la secuencia en una sola fórmula. Sin embargo en realidad es una fórmula, la llamada fracción continua.
Por ejemplo, cuando aplicamos el algoritmo euclidiano para el par 211,27 produce la secuencia de coeficiente 7;1,4,2,2. Esta secuencia es capturada por la ecuación:
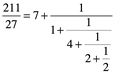
Se obtiene de la siguiente manera:
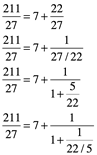
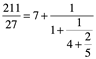
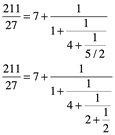
En esta etapa el proceso se detiene porque el resto es 1 y previo divisor es 2, y es exacta. Puesto que el algoritmo euclidiano, produce números que disminuyen en tamaño, por lo tanto, siempre se detiene. Así que cualquier número racional positivo tiene una fracción continua finita. Y por contrario, si una relación de números produce una fracción continua infinita, la relación es irracional. Hasta ahora no habíamos contemplado aplicar el Algoritmo euclidiano para números irracionales… obviamente de proporciones racionales. El resultado es sorprendentemente simple y satisfactorio cuando aplicamos el algoritmo de fracción continua a ![]() y 1.
y 1.
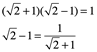
Ahora ocurre esto:
Al aplicar separación entera y parte fraccionaria
![]()
Puesto que![]()
![]()
No hay necesidad de ir más allá, el denominador ![]() a la derecha ahora puede ser sustituido por:
a la derecha ahora puede ser sustituido por:
![]()
Así que ![]() ocurre de nueva vez y así sucesivamente. Por lo tanto, el algoritmo de fracción continua nunca se detendrá.
ocurre de nueva vez y así sucesivamente. Por lo tanto, el algoritmo de fracción continua nunca se detendrá.
El ![]() es irracional, y por tanto, raíz de dos lo es también. Los griegos sabían que raíz de dos es irracional, por lo que queda la duda si ellos sabían esta demostración. Sin duda, Euclides sabía que el algoritmo euclidiano implica a la irracionalidad. Es posible que los irracionales fueran descubiertos de esta manera.
es irracional, y por tanto, raíz de dos lo es también. Los griegos sabían que raíz de dos es irracional, por lo que queda la duda si ellos sabían esta demostración. Sin duda, Euclides sabía que el algoritmo euclidiano implica a la irracionalidad. Es posible que los irracionales fueran descubiertos de esta manera.
Ejercicio 1: Para los pares de números realizar gcd(n,m) por algoritmo de restas y por la propiedad de división.
1) gcd(53,19)=1
2) gcd(987,61)=1
3) gcd(233,55)=1
4) gcd(177,51)=3
5) gcd(512,42)=2
Ejercicio 2: Obtener la fracción continua para los pares siguientes determinando si es irracional o racional la fracción.
1) par 223,21
2) par 121,13
3) par 172,5
Estimado lector, pero Usted se preguntará de nueva cuenta porqué ampliar el pensamiento matemático cuando el estudiante promedio no puede realizar operaciones aritméticas con números fraccionarios. Ahora toca en este apartado resolver la aritmética de pares ordenados o llamados fraccionarios del tipo a/b.
1. Suma de fracciones
La suma con denominador común:
![]()
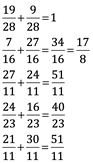
Sustracción con denominador común:
![]()
![]()

La suma con denominador no común:

La substracción con denominador no común:
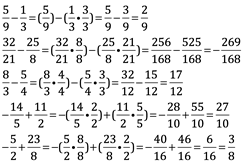
Multiplicación de fracciones:
![]()
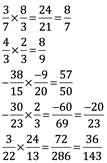
División de fracciones:
![]()
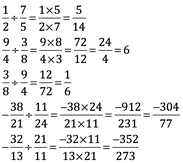
Simplificación de fracciones:
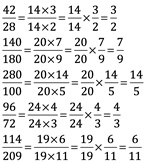
Como muchas ramas de las matemáticas, la historia de la teoría de los números comienza con Euclides. Elements contiene las primeras demostraciones de descenso (la existencia de factorización y terminación del algoritmo euclidiano), la primera prueba de la existencia infinita de los números primos y el primer estudio extenso de números irracionales, Euclides también realizó un gran avance en un tema que ha progresado muy poco desde entonces: números primos de la forma 2n-1 y números perfectos.
Los números enteros positivos se llaman números perfectos si la suma de sus divisores propios positivos (excepto ese mismo número) es equivalente a la cantidad que representan. Por ejemplo, los divisores de 6 son 1, 2 y 3 y 6=1+2+3, por lo que 6 es un número perfecto. Los siguientes números perfectos son:
28, 496, 8128, 33 550 336, 8 589 869 056, 137 438 691 328…,
Euclides descubre que ![]() , es una forma alternativa de escribir un número perfecto, cuando se cumple que
, es una forma alternativa de escribir un número perfecto, cuando se cumple que ![]() es un primo. Su prueba es muy simple, si escribimos p=
es un primo. Su prueba es muy simple, si escribimos p=![]() los divisores apropiados de
los divisores apropiados de ![]() son debido a la factorización única.
son debido a la factorización única.
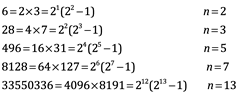
Sí
![]()
y
![]()
La suma del primer grupo es ![]() , y la suma del segundo grupo es:
, y la suma del segundo grupo es:
![]()
por lo que es la suma de los divisores propios [divisores propios, se dice de un número entero b que es divisible entre un número entero a (distinto de cero) si existe un entero c tal que b=a x c]
![]() será necesario.
será necesario.
Todavía no sabemos sobre una descripción clara de los números primos de la forma ![]() . Menos aún sabemos, si hay infinitamente muchos de ellos. Y, finalmente, no sabemos si hay algún número perfecto impar en todos ellos. Menos aún se sabe de los números primos de la forma
. Menos aún sabemos, si hay infinitamente muchos de ellos. Y, finalmente, no sabemos si hay algún número perfecto impar en todos ellos. Menos aún se sabe de los números primos de la forma![]() , pero vale la pena mencionar porque desempeñan un papel inesperado en un problema geométrico antiguo: la construcción regular de m-gons con regla y compás[21]. Euclides dio construcciones de polígonos regulares de m=3 (triángulo equilátero) y m=5 (Pentágono regular) y para valores de m se deriva de estos por tomar su producto y doblar varias veces el número de partes, Gauss construyó un 17-gons (polígono regular de 17 lados) en 1796. Un polígono generalizado es una estructura m-gons de estructura de incidencia introducida por Jacques Tits en 1959.
, pero vale la pena mencionar porque desempeñan un papel inesperado en un problema geométrico antiguo: la construcción regular de m-gons con regla y compás[21]. Euclides dio construcciones de polígonos regulares de m=3 (triángulo equilátero) y m=5 (Pentágono regular) y para valores de m se deriva de estos por tomar su producto y doblar varias veces el número de partes, Gauss construyó un 17-gons (polígono regular de 17 lados) en 1796. Un polígono generalizado es una estructura m-gons de estructura de incidencia introducida por Jacques Tits en 1959.
Una estructura de incidencia es un triple (P, L, I) donde P es un conjunto cuyos elementos se llaman puntos, L es un conjunto disjunto cuyos elementos se llaman líneas y I ⊆ P × L[22] es la relación de incidencia simétrica[23].
 13.08.11.png)
La clase del descubrimiento del patrón de Gauss es que 3, 5 y 17 son primos de la forma
![]() es decir,
es decir,

Gauss encontró de hecho que los polígonos construibles con un número primo de lados, son aquellos para los cuales el primo es de la forma ![]() . Puede ser demostrado fácilmente que los primos son realmente de la forma
. Puede ser demostrado fácilmente que los primos son realmente de la forma ![]() , pero solo cinco de ellos son conocidos:
, pero solo cinco de ellos son conocidos:
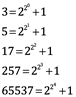
Así, a pesar de que Euclides probo que hay infinitamente muchos números primos, los intentos de encontrar primos de las formas ![]() y
y ![]() , han sido un fracaso rotundo. No cabe duda que los primos son el concepto más sencillo y difícil en las matemáticas, por que son, probablemente, el concepto que mejor resume la naturaleza de las matemáticas en sí mismas. Les vemos aparecer otra vez, en los lugares donde las matemáticas son particularmente interesantes y difíciles.
, han sido un fracaso rotundo. No cabe duda que los primos son el concepto más sencillo y difícil en las matemáticas, por que son, probablemente, el concepto que mejor resume la naturaleza de las matemáticas en sí mismas. Les vemos aparecer otra vez, en los lugares donde las matemáticas son particularmente interesantes y difíciles.
Los números primos son los enteros positivos fáciles de definir, pero difíciles de comprender, son mayores de 1 que no son productos de enteros positivos más pequeños. Así la secuencia de números primos comienza con:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997
Cada número entero positivo n puede factorizarse en números primos, porque si n no es primo, es un producto de números enteros más pequeños a y b, nosotros podemos repetir el argumento con a y b: si cualquiera de ellos no es primo, entonces el producto son números enteros positivos más pequeños y así sucesivamente. La factorización de primos es una pendiente finita. En resumen, los números primos no incluyen al 1, porque este es la unidad, y ni es primo ni es compuesto. Un número compuesto es el que se obtiene multiplicando otros dos números. Todos los primos son impares excepto el 2, que es el único par encontrado. La factorización prima de números mayores a 1, es única sin importar el orden de los factores, por eso 1 no se considera primo. Pero, para retomar ahora las pendientes infinitas descendentes, citaremos a Fibonacci 1202 y Fermat 1670. Fibonacci utilizó el método para encontrar lo que ahora se llaman fracciones egipcias. Los antiguos egipcios tenían una curiosa manera de tratar con fracciones escribiendo a cada fracción entre 0 y 1 como la suma de las distintas fracciones de la forma 1/n, llamada fracción unidad.
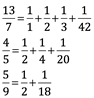
No es difícil encontrar fracciones como estas por ensayo y error, pero cómo podemos estar seguros. Fibonacci dio un método que puede ser probado para alcanzar el éxito, es decir, varias veces elimina la fracción más grande de la unidad. El método de Fibonacci siempre funciona porque, si un b es una fracción en su mínima expresión y 1/n es la fracción más grande de la unidad menos que a/b, entonces:
![]()
Es tal que ![]() . Si
. Si ![]() luego
luego ![]() , por eso que 1/n no es la más grande fracción de unidad menos que a/b. Así el numerador del resto disminuye continuamente hasta detenerse (necesariamente en 1) en un número finito de pasos. Aquí mostramos como es esto para 5/7:
, por eso que 1/n no es la más grande fracción de unidad menos que a/b. Así el numerador del resto disminuye continuamente hasta detenerse (necesariamente en 1) en un número finito de pasos. Aquí mostramos como es esto para 5/7:
1/2= mayor fracción a la unidad< 5/7
Así que considere:
![]() Note que 3<5
Note que 3<5
Siguiente,
1/5= es mayor fracción < 3/14
considere
![]() Esto se da por terminado.
Esto se da por terminado.
La solución es:
![]()
Otra manera es aplicando el método de James Joseph Sylvester, produce la representación de número racional r = a/b entre 0 y 1 como fracción egipcia:
1. Encontrar la fracción unitaria más ajustada a r pero menor que r. El denominador se puede hallar dividiendo b entre a, ignorando el resto y sumando 1. Si no hay resto, r es una fracción unitaria, así que ya no hay que seguir calculando.
2. Restar la fracción unitaria de r y aplicar de nuevo el paso 1 utilizando la diferencia entre las dos fracciones como r.
Para 5/7
5/7= 0 con algún residuo, entonces la primera fracción unitaria es 1/2
![]()
14/3= 4 con algún resto, entonces la siguiente fracción unitaria es 1/5
![]()
1/70 es una fracción unitaria y se concluye.
Ejemplo 1: para 21/32
21/32= 0 con algún residuo, entonces la primera fracción unitaria es 1/2
![]()
32/5= 6 con algún residuo, entonces la primera fracción unitaria es 1/7
![]()
224/3= 74 con algún residuo, entonces la primera fracción unitaria es 1/75
![]()
1/16800= es una fracción unitaria y se concluye.
Es importante notar que las fracciones egipcias no son la única posibilidad, por ejemplo para 19/20
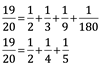
El resultado de Fermat fue considerado más sofisticado que el de Fibonacci, pero similar en su origen. Él probó que no hay ningún entero positivo x,y,z tal que
![]()
Demostrando que cualquier supuesta solución, es una solución más pequeña. Los enteros positivos no pueden disminuir indefinidamente, tenemos una contradicción. Fue Fermat quien introdujo el término descenso de este tipo de prueba. Se aplica la palabra descenso a cualquier prueba que se basa en el hecho de un descenso infinito posible en los números enteros positivos.
Como ya hemos expresado, los irracionales fueron reconocidos hace más de 2 mil años, pero es en los últimos 150 años que los detalles más importantes fueron revelados. En 450 antes de Cristo, los griegos desarrollaron matemáticas puras, desde entonces es constante el nombre que se les dio a los números irracionales, demostrando que el lado y la diagonal de un cuadrado no se pueden medir simultáneamente por la misma unidad o, dicho de otro modo, que la diagonal es inconmensurable con cualquier unidad que se mida el lado. Una responsabilidad moderna para nosotros, es reconciliar lo inconmensurable con lo irracional. Los irracionales irrumpen en la historia para dejar claro que no hay lugar permanente en el mundo de las matemáticas. ¿Qué entendemos por número irracional? Es un número inconmensurable que no se puede expresar como el cociente de dos enteros. O es un número decimal que no es finito ni recurrente. Para ambas definiciones, lo irracional se define en términos de lo que no es, es algo así como definir un número impar de uno que no lo es. Más aún, estas respuestas están plagadas de limitaciones: por ejemplo, ¿cómo las utilizamos para definir igualdad o las operaciones aritméticas entre dos números irracionales? Aunque esto es familiar, las definiciones anteriores son absolutamente inútiles en la práctica. Por ello, los números irracionales están siendo definidos en términos de una de sus cualidades características, no como entidades que no existen. ¿Quiénes somos para decir que todos ellos existen? Por novedad, adoptamos un tercer enfoque:
Puesto que cada número racional k puede ser descrito como:
![]()
Cada número racional es equidistante de los otros dos números racionales (en este caso k+1, k-1); por tanto, ningún número racional es tal que sea una distancia diferente de todos los demás números racionales.
Con esta observación definimos los números irracionales como: el conjunto de todos los números reales con diferente distancia de todos los números racionales.
El conjunto de los números racionales es del mismo tamaño que el conjunto de números enteros, pero los números racionales son mucho más numerosos. Este problema estuvo a fuego lento durante siglos, en el siglo XIX matemáticos más rigurosos examinaron este hecho. De regreso a los griegos, “todas las cosas son números” era la máxima de Pitágoras y central a su filosofía. Número significó solo los discretos enteros positivos, con 1 como unidad por el que fueron medidos todos los otros números. Esto significó que todos los pares de números eran múltiplos de la unidad; es decir, todos los pares de números eran conmensurables por la unidad. En contraste, longitudes, áreas, volúmenes, masas…, eran cantidades continuas, las magnitudes físicas sirvieron a los griegos en lugar de los números reales. Cocientes discretos eran expresiones seguras y su magnitud se podría prever también, siempre que los dos valores afectados fueran del mismo tipo. Además, la declaración de proporciones A/B=C/D donde en un lado de la igualdad se encuentran magnitudes de un tipo y del otro de otro tipo. El estudio de los números irracionales en las escalas musicales reveló que estas coinciden con la armonía musical de los sonidos, medidos como radios de números enteros de longitudes de cuerda, por ejemplo, la octava corresponde a una relación de longitud de 2 a 1 y un perfecto 3 a 2. Esto evidencia la continuidad, que se podría medir en forma discreta. Se corroboró que las modificaciones y las proporciones de las escalas musicales eran expresables en números; desde entonces, todo lo demás parecía en su naturaleza entera para modelar en números los cielos y las cosas como sí fueran proporciones o escuelas que demuestran que la realidad son números.
Con este dogma Pitagórico, todo estaba listo para una fuerte crisis matemática de auténtico escándalo lógico. Entre Antioch y Proclus atribuyeron la definición de ángulo como una cantidad, específicamente la distancia entre líneas o planos. Con la autoridad de Proculos, Thales, el primero de los siete sabios de la tradición griega, trajo de Egipto a Grecia los siguientes postulados geométricos:
1. Un círculo es atravesado por cualquier diámetro.
2. Los ángulos de la base de un triángulo isósceles son iguales.
3. Los ángulos entre dos rectas que se cruzan son iguales.
4. Dos triángulos son iguales si tienen dos ángulos y un lado igual.
 14.00.11.png)
Estos parecen desde nuestro tiempo logros muy modestos, sin embargo, su simplicidad desmiente su significado, como exhiben el germen de los procedimientos deductivos de la filosofía griega, recuerde que aún civilizaciones egipcias y babilónicas no tenían ningún pensamiento axiomático, abstracto o generalizado para resultados matemáticos. Estas recetas individuales son desde luego muy importantes, pero no son resultado de un proceso deductivo. Para darnos una idea de la magnitud de las recetas de Thales, deberíamos estudiar la enorme aplicación que ha significado el Teorema de Pitágoras. Con esto, la dirección del progreso matemático fue determinada como la cuna de la ciencia, al presentar las bases del razonamiento deductivo para inferir conclusiones lógicas.
El innombrable inconmensurable, estaba listo para crear una crisis matemática sin precedente. Tenga presente que los griegos llamaron al inconmensurable lo que hoy llamamos número irracional. Tengamos presente que para los pitagóricos todas las cosas existentes son números, la propia existencia es un número, y además introducen los términos: magnitud, longitud, área, volumen, lo que significó que no solo fueron notas musicales. Cualquier longitud era conmensurable entre sí, es decir, dadas dos líneas de diferente longitud, para los pitagóricos allí debe existir una tercera línea la cuál es su común unidad. En notación moderna, ![]() y
y ![]() con unidad común u, deben existir enteros
con unidad común u, deben existir enteros ![]() y
y ![]() tales que:
tales que:
![]()
![]()
La consecuencia de esto es que
Çç la relación entre dos magnitudes cualquiera es el cociente de dos enteros.
![]()
Y la conveniencia del dogma filosófico depende de este resultado. En notación moderna, la unidad se llama monada, el proceso de demostración es:
![]()
Nos da:
![]()
La media aritmética;
![]()
Nos da
![]()
La media geométrica.
![]()
Nos da:
![]()
La media harmónica.
Con la fórmula de la media geométrica:
![]()
Tenemos la aparición de ![]() .
.
Dicho esto, se le atribuye a Hippasus de Metapontum, se le acusa de haber destruido el concepto de conmensurabilidad que rompió el dogma hermético de Pitágoras y fue Proclus quien respaldó este hecho, sacudiendo los cimientos de una realidad continua, algo semejante a la teoría cuántica que hace ver en forma discreta la realidad. Los pitagóricos habían hecho encajar la idea de que el mundo es algo cuantificable o medible, como forma cosmológica continua, pero los inconmensurables como cociente de dos magnitudes, significa que la herramienta geométrica fundamental se asemeja a un acto de probar la existencia. Los inconmensurables Platón los refirió como inmencionables, quizá con la idea de ocultar el poder de este descubrimiento respecto al mundo religioso. El método de prueba sobre raíz de dos, es un misterio, se cree que se realizó mediante un cuadrado de lado uno y de alguna manera al intentar demostrar su longitud diagonal se descubre que es inconmensurable, así lo mencionó el Libro Elements. En forma moderna supongamos que:
![]()
Donde a y b son números enteros en sus términos más bajos. Luego:
![]()
Así que ![]()
Si escribimos a=2k, entonces:
![]()
y
![]()
Por lo tanto, en su forma geométrica se esconde su belleza inherente de la discusión.
Desde este punto los griegos no hicieron nada para abrazar a los irracionales, habían evitado tanto como les fuera posible utilizar la geometría para sobrellevar a estos números, los romanos tampoco hicieron nada para adelantar en esta materia el pensamiento sobre los irracionales. Si queremos continuar con el avance histórico de estos números, tendremos que mirar a las civilizaciones Hindú y Árabe. Para los primeros, investigar la matemática no fue un deseo de pureza abstracta como lo fue para los griegos, sino una mezcla de las necesidades de hacer frente a la práctica contable, astronomía y astrología. Y además, el deseo de entender la teoría del sistema numérico; de ellos fue la aceptación del cero como el conjunto vacío y neutro entre positivos y negativos, y al adoptar esta concepción perfeccionaron el sistema de posiciones base 10 y desarrollaron las raíces cuadradas de números. Esto no significó el progreso filosófico respecto a los irracionales, solo fueron aceptados como números y manipulados de la misma manera que los racionales, creando la aritmética irracional. Para estos antiguos Hindúes no implicó una raíz cuadrada, para estos dos enteros a y b su prescripción resulta en:
![]() Y así:
Y así:
![]()
Por supuesto la idea era crear cuadrados perfectos al introducir un factor, que solo es posible si todos los factores primos a y b aparecen con la misma paridad en su potencia. Si tomamos a=3 y b=12, podemos tomar a c=12 para que ocurra:
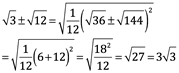
Esto resulta complicado para nuestra mirada moderna, pero ciertamente fue una idea de nueva perspectiva.
![]()
Es decir:
![]()
Otra vez empleando el ejemplo anterior:
![]()
Los Hindúes desarrollaron estas equivalencias:
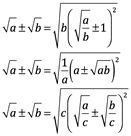
A su manera los hindúes podían manipular los números irracionales de la forma de raíces cuadradas de números enteros no cuadrados.
Pero fueron los Árabes los que introducen los conceptos de álgebra y algoritmo por ejemplo. Fue el desarrollo del álgebra, el que provoco significativamente el uso de números irracionales difuminó la distinción entre tipos de números: enteros, racionales o irracionales, estos últimos tratados como raíz de un tipo de ecuación; el manipular la ecuación implica emplear números de este tipo.
Leonardo Bonacci, Leonardo Bigollo o Leonardo Pisano, o más reconocido en nuestro tiempo como Fibonacci (1170-1250 d.c.). Fibonacci se hace famoso por aportar una secuencia de números para el problema de cría de conejos, pero él fue un gran teórico de los números y desde niño aprendió el sistema hindú de numeración decimal y en sus viajes a Medio Oriente se hace de conocimientos matemáticos desconocidos en Europa. El cero y la noción de serie numérica pronto los reconoce como de enorme ventaja para hacer avanzar a la humanidad en el terreno aritmético. El tratamiento de los números inconmensurables de Euclides en particular le despertó enorme curiosidad, se planteó encontrar la raíz (única verdadera) de la ecuación:
![]()
Sus argumentos establecen rápidamente que tal raíz no puede ser integral o racional, por otra parte, no podrá tomar cualquier forma dicha en el Libro X de Euclides Elements, y como tal representa un nuevo tipo de número irracional, que no es asequible de construcción por escuadra y compás, haciéndose eco por Omar Khayyam quien afirmó que efectivamente no era posible resolver la ecuación por todo lo conocido hasta ese momento.
Las soluciones encontradas las estimo en un sistema sexagesimal:
![]()
Es una aproximación racional a nueve lugares decimales de exactitud para el número irracional:
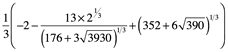
La propia naturaleza cíclica de los objetos celestes requiere que sus movimientos sean conmensurables unos respecto de otros; una prueba contraría destruiría la exactitud de las repeticiones y así el año no sería perfecto. El argumento supone que dos cuerpos se mueven hacia adelante y hacia atrás a la misma velocidad, uno a lo largo del lado y el otro en la diagonal de un cuadrado (con implícito cambio instantáneo de la dirección; si cada uno de ellos sale desde la misma esquina al mismo tiempo), entonces su regreso simultáneo a esa esquina requiere la existencia de los números positivos n y m hasta que ![]() , con la irracionalidad de esta representación imposible se tambalea la exactitud. Sin embargo, admitió Fibonacci que llevar esta discusión a los movimientos de los cuerpos celestes requiere una gran discusión. El que estuvo dispuesto a esta empresa fue Edward III arzobispo de Canterbury, tomando la idea de Aristóteles que creía que el cociente de la fuerza a la resistencia de un objeto es proporcional a la velocidad lograda de tal modo, una visión falsa, sería decir que un aumento geométrico en el cociente de esa fuerza de resistencia resulta en una aritmética de incremento en velocidad. John Duns Scotus argumentó, que si las velocidades de dos objetos celestes eran inconmensurables entre sí, entonces así sería la distancia a la que viajarían en periodos de tiempo iguales y esto les haría volver a cierta configuración inicial en algún tiempo futuro imposible. En términos de la ecuación de Bradwardine para los coeficientes de las fuerzas (desconocidas) y las resistencias se espera para el exponente que la fracción de la velocidad sea un número irracional.
, con la irracionalidad de esta representación imposible se tambalea la exactitud. Sin embargo, admitió Fibonacci que llevar esta discusión a los movimientos de los cuerpos celestes requiere una gran discusión. El que estuvo dispuesto a esta empresa fue Edward III arzobispo de Canterbury, tomando la idea de Aristóteles que creía que el cociente de la fuerza a la resistencia de un objeto es proporcional a la velocidad lograda de tal modo, una visión falsa, sería decir que un aumento geométrico en el cociente de esa fuerza de resistencia resulta en una aritmética de incremento en velocidad. John Duns Scotus argumentó, que si las velocidades de dos objetos celestes eran inconmensurables entre sí, entonces así sería la distancia a la que viajarían en periodos de tiempo iguales y esto les haría volver a cierta configuración inicial en algún tiempo futuro imposible. En términos de la ecuación de Bradwardine para los coeficientes de las fuerzas (desconocidas) y las resistencias se espera para el exponente que la fracción de la velocidad sea un número irracional.
Por supuesto, para ese tiempo no había esperanza de acercarse a demostrar rigurosamente esto y se recurrió a un salto casi de fe, extrapolando un caso práctico de aritmética finita a la gran complejidad del movimiento celeste visto desde el año 1350. Sin embargo, este argumento no destruyó la creencia de un año perfecto, pero lo podemos considerar como una de las primeras declaraciones de que los irracionales están presentes en la realidad.
El fraile italiano Franciscano Luca Pacioli (1487) escribió para la “divina proporción: Justo como Dios no puede ser correctamente definido, ni puede ser entendido a través de palabras, esta proporción señala además a través de números inteligibles, que no puede ser expresada a través de cualquier cantidad racional, pero siempre permanece oculta y en secreto, y los matemáticos le llaman irracional”[24].
Michael Stifel (1544) en su aritmética integra dijo: “con razón se discute si los números irracionales son números verdaderos o falsos. Ya que, en el estudio de figuras geométricas, donde nos fallan números racionales, los irracionales tienen su lugar y demostración; exactamente aquellos números que no pueden ser probados… estamos movidos y obligados a admitir que realmente son números, obligados por los resultados que se derivan del movimiento celeste. Por otro lado, otras observaciones nos obligan a no considerarlos números. A saber, cuando tratamos de someter a números para evadir a los irracionales… Ahora podemos llamar número real a la naturaleza que carece de precisión. Por lo tanto, tal como un número infinito no es un número, un número irracional no es un número verdadero, pero se encuentra oculto en una especie de nube infinita”.
En cuanto a pi:
“Por lo tanto, el círculo matemático se describe acertadamente como el polígono regular de infinitos números de lados. Y así la circunferencia matemática no requiere de números racionales o irracionales”[25].
Pero finalmente Simon Stevin 1585 fue quien introduce a Europa el sistema decimal Árabe-Hindú y la aritmética de enteros, fracciones e irracionales, así como algo de álgebra polinomios y teoría de las ecuaciones. Para él, 1 era un número, pero cero no fue reconocido como número, aunque los negativos fueron acogidos, los números complejos fueron desechados. Además, él hizo del punto euclidiano algo más al referirlo como un concepto de continuidad[26] al compararlo con un flujo de agua y cada una de sus magnitudes que corresponde a una serie continua. Era impensable que la recta numérica o un plano tuviese perforaciones de caídas descendentes de números irracionales.
Frenchmen Pierre de Fermat (1601-65) y René Descartes (1596-1650) en común matemáticos y filósofos, quizá también compartieron una actitud escéptica. Fermat comúnmente al escribir ecuaciones enseguida investigaba su curva asociada. Descartes escogía una curva conocida e intentaba encontrar la ecuación asociada en términos de “x” y “y”. Con el advenimiento de la geometría analítica fue necesario resolver ecuaciones, que eran equivalentes a sus problemas geométricos asociados, pero a menudo estos presentaron raíces irracionales; apenas fue un problema nuevo, pero que ahora asume el momento histórico de mayor desafío práctico. Por ejemplo, el problema de encontrar la distancia entre dos puntos en el plano, con la prevalencia de irracionales cuadráticos, a pesar de que los puntos pueden ser coordenadas racionales, la distancia entre ellos es probablemente un irracional para:
![]()
Si suponemos una táctica para evitar números irracionales en el conjunto, es decir, solo considerar distancias racionales en el plano. Ahora, supongamos que podemos elegir tres puntos distintos para formar los lados de un triángulo con lados racionales, entonces el coseno con notación estándar tiene que ser:
 14.41.43.png)
![]()
Este cociente es el ángulo de rotación del triángulo. Si A es racional medido en grados, los valores cos A serán:
![]()
Los valores aceptables serian 60º y 90º ya que el mismo cociente debe ser válido para los tres ángulos, para 60º el triángulo es equilátero. En definitiva, los únicos posibles triángulos con lados racionales deben ser equiláteros.
Pasamos ahora a un círculo unitario.
![]()
En su forma paramétrica estándar:
![]()
Sabemos que contiene un número infinito de puntos racionales, con la parametrización todos ellos con parámetro t varían sobre todos los números racionales. Sin embargo, hay un número infinito de puntos en el círculo de al menos una coordenada que es irracional. ¿Pero importa esto? Tratando de encontrar la intersección de ![]() con la línea y=x se revela rápidamente que los números irracionales no se pueden evitar.
con la línea y=x se revela rápidamente que los números irracionales no se pueden evitar.
Por ejemplo, el círculo ![]() , otra vez tiene infinitos puntos racionales y al menos una coordenada irracional, Usted lo puede comprobar verificando en su forma parametrizada rotando el valor de t.
, otra vez tiene infinitos puntos racionales y al menos una coordenada irracional, Usted lo puede comprobar verificando en su forma parametrizada rotando el valor de t.
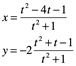
Para ![]() no hay un solo punto racional por no haber parametrización racional. En fin, con el nacimiento del álgebra geométrica, los números irracionales eran por lo menos implícitamente y explícitamente a menudo indispensables. El cálculo diferencial e integral que pronto nacerían necesitarían de una noción de curva geométrica, surgida de rectas que pertenecen a círculos, los círculos son llamados polígonos regulares de n lados. Actualmente el problema de los irracionales se trasladó a lo que ahora conocemos como integración, en el continuo de cálculos sobre áreas bajo la curva aparecen los irracionales de nueva cuenta. El uso de infinitesimales hace conciencia de que un número de raíces inconmensurables entre sí, podrían reunir en una suma una relación que explica cantidades racionales, como si la infinitud misma de sumas de áreas infinitesimales destruyera de su interior la irracionalidad.
no hay un solo punto racional por no haber parametrización racional. En fin, con el nacimiento del álgebra geométrica, los números irracionales eran por lo menos implícitamente y explícitamente a menudo indispensables. El cálculo diferencial e integral que pronto nacerían necesitarían de una noción de curva geométrica, surgida de rectas que pertenecen a círculos, los círculos son llamados polígonos regulares de n lados. Actualmente el problema de los irracionales se trasladó a lo que ahora conocemos como integración, en el continuo de cálculos sobre áreas bajo la curva aparecen los irracionales de nueva cuenta. El uso de infinitesimales hace conciencia de que un número de raíces inconmensurables entre sí, podrían reunir en una suma una relación que explica cantidades racionales, como si la infinitud misma de sumas de áreas infinitesimales destruyera de su interior la irracionalidad.
El número es:
![]()
Este número es atribuido a Jacob Bernoulli (1654-1705[27]) y Leonhardo Euler. Euler sabía que la forma de fracción continua simple de un número irracional es infinita. Para demostrar un irracional se necesita construir una fracción continua para ver sí desciende de manera infinita y poder asegurar que nps encontramos frente a un irracional.
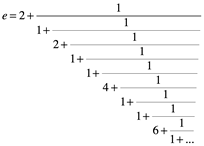
2.71828182845904
El número e en forma de fracción continua y en forma de decimal con 14 dígitos
Resulta extraño que Euler no hubiera detectado que la irracionalidad de e era una consecuencia inevitable de su representación canónica como serie infinita, bien conocida por él.
![]()
Fue Joseph Fourier, quien relaciona la irracionalidad de un número a la serie infinita de su representación.
Hemos descubierto hasta aquí los números trascendentales:![]() . Un modo de comprobar su designación reside en la serie infinita de su representación. Si la expansión decimal de un número a/b es finita, entonces es un racional. Si la expansión decimal de un número a/b es infinita, entonces es irracional.
. Un modo de comprobar su designación reside en la serie infinita de su representación. Si la expansión decimal de un número a/b es finita, entonces es un racional. Si la expansión decimal de un número a/b es infinita, entonces es irracional.
1.4 Los números reales
Estos números reales son el cuerpo o campo cerrado bajo una operación binaria (+,x), llamando a esta álgebra aritmética, cuyas propiedades son:
 16.36.20.png)
 16.50.08.png)
Definiciones:
Los números naturales ![]() son los que van del 1 hacia el infinito: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11… es decir, son números positivos que sirven como índice para contar los elementos de un conjunto.
son los que van del 1 hacia el infinito: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11… es decir, son números positivos que sirven como índice para contar los elementos de un conjunto.
Un número entero ![]() es cualquier elemento del conjunto formado por los números naturales, sus opuestos (versiones negativas de los naturales) y el cero. Estos son: Los naturales (o enteros positivos): +1, +2, +3, +4, +5... El cero, que no es ni positivo ni negativo.
es cualquier elemento del conjunto formado por los números naturales, sus opuestos (versiones negativas de los naturales) y el cero. Estos son: Los naturales (o enteros positivos): +1, +2, +3, +4, +5... El cero, que no es ni positivo ni negativo.
Los números racionales ![]() hacen referencia a aquellos a/b que permiten conocer el cociente entre dos números enteros. También llamados fraccionarios.
hacen referencia a aquellos a/b que permiten conocer el cociente entre dos números enteros. También llamados fraccionarios.
El conjunto de los números irracionales ![]() se representa por a/b y está formado por todos los números decimales cuya parte decimal tiene infinitas cifras periódicas, es decir, por todos los números que no se pueden representarse por el cociente de dos números enteros.
se representa por a/b y está formado por todos los números decimales cuya parte decimal tiene infinitas cifras periódicas, es decir, por todos los números que no se pueden representarse por el cociente de dos números enteros.
1.5 Potencias
Un número es un conjunto que expresa la cantidad de sus elementos. Esperamos que A siendo un número, sea un conjunto finito. Dado un conjunto A, a la colección de todos los subconjuntos de A se denominan conjuntos de potencia de A. Si lo escribimos así P(A); o otra notación más común es por ejemplo para el número dos: ![]() .
.
Si ![]() , entonces P(A)={0,1,2,3}
, entonces P(A)={0,1,2,3}
El conjunto de potencias parte del conjunto vacío, un conjunto cuyo elemento único es el vació. ![]() =1 Todo conjunto de potencias contiene a la potencia cero, donde solo tiene un elemento. Todo número a la cero por tanto, es igual a uno.
=1 Todo conjunto de potencias contiene a la potencia cero, donde solo tiene un elemento. Todo número a la cero por tanto, es igual a uno.
Si A=1 la Potencia P(A)= ![]() =2
=2
Si A=2 la Potencia P(A)= ![]() =4
=4
Si A=3 la Potencia P(A)= ![]() =8
=8
A es un conjunto finito de n elementos. P(A) es un conjunto finito de ![]() elementos. Si n=0 entonces P(A)=1. Esto es verdadero por inducción para todos los números elevados a la potencia cero.
elementos. Si n=0 entonces P(A)=1. Esto es verdadero por inducción para todos los números elevados a la potencia cero.
Potencia de un número a, es el producto de este tantas veces n.
![]() , n veces.
, n veces.
Donde x, es producto del factor a, n veces.
El signo de ![]() es positivo si es par y negativo si es impar.
es positivo si es par y negativo si es impar.

Si P(A) + P(A) = ![]()
Si P(P(A))=![]()
Si P(A) donde no tienen porque ser solo positivos a y n.
![]()
Pero a y n no necesariamente deben ser solo número enteros positivos, podrían ser cualquier número real o complejo.
Un tema relacionado con las potencias es el de factorial de un número.
Sea ![]() el número de formas de muestrear k veces desde un conjunto n de elementos. Donde el resultado m factorial es definido como:
el número de formas de muestrear k veces desde un conjunto n de elementos. Donde el resultado m factorial es definido como:
![]()
3!=3x2x1=6
12!=12x11x10x9x8x7x6x5x4x3x2x1=479001600
Cuando se desea trabajar con números elevados a una potencia de base 10, esta notación exponencial generalmente nos conduce a la notación científica de los números.
1.6 Radicación
La raíz ![]() (es un signo de radical), si y solo si bn=a. Donde a es la cantidad radicando, exigiendo esta ser positiva en los reales, caso contrario será una cantidad imaginaria y, n es el índice del radical o grado del radical. Es una operación inversa del exponencial. Si la expresión es racional la raíz es exacta y si no es irracional. Un radical tiene tantas raíces como el grado del radical. El valor aritmético del radical puede ser resuelto para un
(es un signo de radical), si y solo si bn=a. Donde a es la cantidad radicando, exigiendo esta ser positiva en los reales, caso contrario será una cantidad imaginaria y, n es el índice del radical o grado del radical. Es una operación inversa del exponencial. Si la expresión es racional la raíz es exacta y si no es irracional. Un radical tiene tantas raíces como el grado del radical. El valor aritmético del radical puede ser resuelto para un ![]() . Por ejemplo
. Por ejemplo ![]() . Además de las leyes de los exponentes agregaremos las de los radicales:
. Además de las leyes de los exponentes agregaremos las de los radicales:
![]()
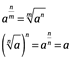
![]()
1.7 Notación científica
La notación científica es una forma de expresar números como el producto de dos números: un coeficiente y el número 10 elevado a una potencia. Es una herramienta muy útil para trabajar con números que son muy grandes o muy pequeños. Como ejemplo, 160,000,000,000 metros, una distancia muy grande. En notación científica, la distancia se escribe como 1.6 × 1011 m. El coeficiente es 1.6 y debe ser un número mayor o igual que 1 y menor que 10. La potencia de 10, exponente 11, tendría que multiplicar 1.6 por 1011 para obtener el número correcto. La notación científica se refiere a veces como notación exponencial. Un resumen de las unidades del Sistema Internacional de Unidades SI se da en la tabla a continuación. Observe que cuando son números pequeños el exponencial es negativo.
 14.49.40.png)
Para escribir un número grande en notación científica, primero debemos mover el punto decimal al primer número de la cifra entre 1 y 10. Como mover el punto decimal cambia el valor, tenemos que aplicar una multiplicación por la potencia de 10 que nos resulte en un valor equivalente al original. Para encontrar el exponente, solo contamos el número de lugares que recorrimos el punto decimal. Ese número es el exponente de la potencia de 10. De la forma ax10n donde a ![]() o
o ![]() y n es un entero.
y n es un entero.
Por ejemplo:
54,000,000.00 a notación científica: 5.4x107
0.0007 a notación científica: 7x10-4
El teorema fundamental del Aritmética dice: cada número natural o es primo o puede ser escrito como un producto de primos. Este teorema no lo abordaremos dado que esta fuera de nuestro alcance curricular, pero nos permite darnos cuenta que hay una factorización única para cada número natural y que la aritmética es un campo fascinante que no termina en este enfoque tan básico expuesto aquí.
1.8 El plano complejo
Los números reales ![]() incluyen a los racionales e irracionales, que corresponden a todos los puntos de una línea infinita llamada línea real. Parece indiscutible que el cuadrado de un número negativo es positivo, puesto que el cuadrado de un número real es no negativo, cumpliendo la ecuación:
incluyen a los racionales e irracionales, que corresponden a todos los puntos de una línea infinita llamada línea real. Parece indiscutible que el cuadrado de un número negativo es positivo, puesto que el cuadrado de un número real es no negativo, cumpliendo la ecuación:
![]()
Es Raphael Bombelli en 1526 quien introduce el número complejo, fue en su obra L’Algebra[28], donde se observa a simple vista que la ecuación anterior no tiene ninguna solución real (raíces). Sin embargo, Roger Penrose destaca que, al superarse concebirlo imposible, por un enfoque razonable que exige otro sistema de números que sea adecuado para tales propósitos, en que nos permita resolver la ecuación?[29]![]() . Para este caso la ecuación algebraica general de grado n, donde
. Para este caso la ecuación algebraica general de grado n, donde ![]() son números reales cualesquiera.
son números reales cualesquiera.
![]()
Este objetivo solo puede lograrse si conseguimos extender el sistema de números reales por otro que es parte, lo hacemos con un sistema de numeración de otro más extendido. ![]() es en cierto sentido la ecuación algebraica más simple sin raíces reales, un primer acercamiento evidente para nuestro problema es introducir una unidad imaginaria
es en cierto sentido la ecuación algebraica más simple sin raíces reales, un primer acercamiento evidente para nuestro problema es introducir una unidad imaginaria![]() , es decir, una nueva dimensión y entonces el plano numérico se extiende al número complejo de la forma:
, es decir, una nueva dimensión y entonces el plano numérico se extiende al número complejo de la forma:
![]() ,
,
Donde a y b son números reales arbitrarios y la operación de estos números se define de manera natural como binomios ![]() donde x es desconocida, salvo en este caso:
donde x es desconocida, salvo en este caso:
![]()
Sí b=0, observamos que solo está presente la línea real con sus características especiales. Asombrosamente como veremos resulta que una vez que permitimos que x tome valores complejos, la ecuación general algebraica siempre tiene una raíz, aunque los coeficientes ![]() sean números complejos, un resultado que es conocido como el teorema fundamental del álgebra: establece que todo polinomio de grado mayor que cero tiene una raíz.
sean números complejos, un resultado que es conocido como el teorema fundamental del álgebra: establece que todo polinomio de grado mayor que cero tiene una raíz.
Por número complejo nos referimos a una expresión![]() , donde a y b son números reales e “i” es la unidad o dimensión imaginaria. Si a es la parte real de c, escrita como Re c, b es llamada la parte imaginaria de c, escrita como Im c. El número complejo cero es
, donde a y b son números reales e “i” es la unidad o dimensión imaginaria. Si a es la parte real de c, escrita como Re c, b es llamada la parte imaginaria de c, escrita como Im c. El número complejo cero es ![]() , donde las partes imaginaria y real valen cero. Por definición dos números
, donde las partes imaginaria y real valen cero. Por definición dos números ![]() son iguales solo sí
son iguales solo sí
![]()
Si Im c=0, c=a+bi se reduce a un número real, mientras que ![]() , se dice que c es puramente imaginario. Los números complejos pueden ser representados geométricamente como puntos en el plano, un hecho que no solo es útil, sino prácticamente indispensable para la ingeniería y la aplicación científica moderna de este “mágico número”, como lo llama Roger Penrose. Con la introducción de un sistema de coordenadas rectangulares en el plano, podemos identificar el número complejo
, se dice que c es puramente imaginario. Los números complejos pueden ser representados geométricamente como puntos en el plano, un hecho que no solo es útil, sino prácticamente indispensable para la ingeniería y la aplicación científica moderna de este “mágico número”, como lo llama Roger Penrose. Con la introducción de un sistema de coordenadas rectangulares en el plano, podemos identificar el número complejo ![]() , como
, como![]() , asociado con el punto P.
, asociado con el punto P.
De esta manera, establecemos una correspondencia biunívoca entre el conjunto de todos los números complejos y el conjunto de todos los puntos en el plano con una precisión infinita dado que las partes Re y Im son números racionales e irracionales. Claramente, con esta asignación, el conjunto de todos los números reales en el eje x y el conjunto de los números puramente imaginarios en el eje y, mientras que el conjunto de los números ![]() corresponden al plano complejo o llamado plano z, en el entendido que tal plano z es construido por términos
corresponden al plano complejo o llamado plano z, en el entendido que tal plano z es construido por términos ![]() que son los puntos que definen la densidad de la superficie z. Otra manera de representar al número complejo es usar el vector posición que une el origen con algún punto en el plano z[30]. El vector
que son los puntos que definen la densidad de la superficie z. Otra manera de representar al número complejo es usar el vector posición que une el origen con algún punto en el plano z[30]. El vector ![]() cuyo módulo o norma está dado por el valor absoluto del número complejo z, denotado por
cuyo módulo o norma está dado por el valor absoluto del número complejo z, denotado por ![]() . El ángulo de dirección entre el eje real y el vector
. El ángulo de dirección entre el eje real y el vector ![]() , es positivo solo si la rotación es en el sentido antihorario y negativo en el sentido contrario; se llama argumento del número complejo z y se denota por Arg z. En otras palabras
, es positivo solo si la rotación es en el sentido antihorario y negativo en el sentido contrario; se llama argumento del número complejo z y se denota por Arg z. En otras palabras ![]() y
y ![]() son las coordenadas polares
son las coordenadas polares![]() .
.
Por lo tanto:
![]()
![]()
Esta última forma es la que se llama forma trigonométrica de un número complejo z. Claramente Arg z, se define solo en un múltiplo entero de![]() . Sin embargo, existe uno y solo un valor de Arg z, es decir de
. Sin embargo, existe uno y solo un valor de Arg z, es decir de ![]() , que satisface la desigualdad:
, que satisface la desigualdad:
![]()
![]()
donde n se extiende sobre los números enteros positivos y negativos incluyendo al cero.
![]()
y
![]()
Se requiere algún cuidado en invertir la expresión de la tangente, puesto que el arco tangente de un número real x, es escrito como Arc tan x, y se define solo para múltiplos enteros de ![]() . Sin embargo, existe uno y solo un valor de Arc tan x, digamos un
. Sin embargo, existe uno y solo un valor de Arc tan x, digamos un ![]() que satisface la igualdad:
que satisface la igualdad:
![]()
y llamaremos al valor ![]() , el valor principal del arco tangente de x, escrito arc tan x. Nosotros ahora podemos invertir la relación
, el valor principal del arco tangente de x, escrito arc tan x. Nosotros ahora podemos invertir la relación ![]() , obteniéndose:
, obteniéndose:
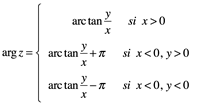
Por otra parte, ![]() se convierte en infinito, claramente si tenemos:
se convierte en infinito, claramente si tenemos:
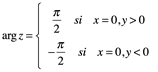
mientras que el caso z=0 es indeterminado como la versión Maya del cero.
Los números complejos
![]()
se dice son números complejos conjugados, si uno de estos se denota por z, y el otro se denota por ![]() o
o ![]() .
.
Obviamente los puntos z y ![]() son simétricos con respecto al eje real x.
son simétricos con respecto al eje real x.
![]()
![]()
Por otra parte
![]()
A menos que z sea un número con la parte real negativa, en cuyo caso:
![]()
La ecuación de Euler o llamada por otros, identidad de Euler:
![]()
donde i es la unidad imaginaria. Tenga en cuenta que la identidad de Euler es poliédrica y a veces también se llama la fórmula sobre una curvatura Euler. La expresión equivalente:
![]()
previamente había sido publicada por Costas (1714). El caso especial de la fórmula con ![]() da la identidad:
da la identidad:
![]()
Una ecuación que conecta los números fundamentales![]() , e, 1 y 0 (cero), las operaciones fundamentales +, ×, y exponenciales, la relación más importante =, y nada más. Gauss comento que esta fórmula no era inmediatamente obvia.
, e, 1 y 0 (cero), las operaciones fundamentales +, ×, y exponenciales, la relación más importante =, y nada más. Gauss comento que esta fórmula no era inmediatamente obvia.
La fórmula de Euler se puede demostrar utilizando un desarrollo de series:
![]()
![]()
![]()
![]()
![]()
![]()
Aplicando a ambos miembros de la igualdad la exponencial:
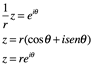
Donde r representa la magnitud de z y es el argumento de z, usualmente llamado arg z.
![]()
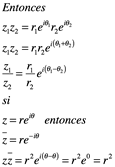
Potencias de complejos
Ejemplo 1. Determine el valor de ![]()
Sabemos que:
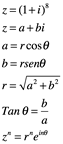
Solución:
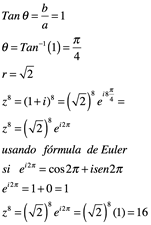
Ejemplo 2. Determine el valor de ![]()
Solución:
![]()
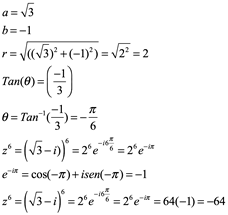
Ejercicio 1. Determine el valor de ![]() escribiendo el procedimiento.
escribiendo el procedimiento.
Solución:
![]()
La ecuación ![]() donde n es el valor complejo de raíces n-esima de la unidad, es decir, se dice “cada raíz tiene una magnitud de”. Ahora que:
donde n es el valor complejo de raíces n-esima de la unidad, es decir, se dice “cada raíz tiene una magnitud de”. Ahora que:
![]()
Usando la ecuación de Euler:
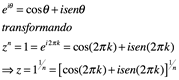
Ahora nosotros usamos la fórmula e De Moivre que establece:
![]()
Así que:
![]()
Donde k es cualquier número entero. Ahora está claro que todas las n raíces de z deben estar en un círculo de radio 1, y las expresiones del tipo ![]() son típicamente de la forma:
son típicamente de la forma:
![]()
Pero en este caso r=1, por lo tanto:
![]()
1.9 Álgebra compleja
Se deduce de su tratamiento como binomiales, suma y producto de dos complejos:
![]()
están dados por:
![]()
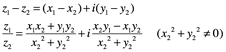
Álgebra compleja es un campo para el que se cumplen las propiedades axiomáticas de toda álgebra, dados los números complejos ![]()
Conmutativa bajo +
![]()
Conmutativa bajo 
![]()
Asociativa bajo +
![]()
Asociativa bajo 
![]()
Distributiva bajo la +
![]()
Distributiva bajo la 
![]()
Elemento neutro bajo la +
![]()
Elemento neutro bajo la 
![]()
Inverso simétrico 
![]()
![]()
![]()
Hasta lo visto aquí, uno podría representar a los números complejos como pares ordenados (sin emplear la unidad imaginaria i);
![]()
donde ![]() son números reales, entonces multiplicación y adición pueden ser representadas:
son números reales, entonces multiplicación y adición pueden ser representadas:
![]()
Con este enfoque, la relación ![]() tiene como análogo:
tiene como análogo:
![]()
Hemos visto que la explicación de la extensión de los números reales a los números complejos no es menos exquisita que la extensión de los números enteros a los racionales y su posterior extensión de los racionales a los irracionales implicados en el concepto de una línea continua.
Ejercicios aritmética de complejos
Ejercicios 1: Represente los siguientes números complejos en su forma trigonométrica:
- 1+i
- -1-i
- 1-i
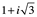
Referencias
[1] Vinogradov, I. M. (2016). Elements of number theory. Courier Dover Publications.
[2] Einstein, A., & Engel, A. (1987). The collected papers of Albert Einstein (7). Princeton University Press.
[3] Pagano, S., Lombardi, L., & Mazza, V. (2014). Brain dynamics of attention and working memory engagement in subitizing. Brain Research, 1543, 244-252.
[4] Menary, R. (2015). Mathematical cognition: A case of enculturation. Retrieved from https://philarchive.org/archive/MENMCA-2
[5] Revkin, S. K., Piazza, M., Izard, V., Cohen, L., & Dehaene, S. (2008). Does subitizing reflect numerical estimation. Psychological science, 19(6), 607-614.
[6] Maloney, E. A., Risko, E. F., Ansari, D., & Fugelsang, J. (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition, 114(2), 293-297.
[7] Piazza, M., Fumarola, A., Chinello, A., & Melcher, D. (2011). Subitizing reflects visuo-spatial object individuation capacity. Cognition, 121(1), 147-153.
[8] Maloney, E. A., Risko, E. F., Ansari, D., & Fugelsang, J. (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition, 114(2), 293-297.
[9] Baddeley, A. (2001). The magic number and the episodic buffer. Behavioral and Brain Sciences, 24(1), 117-118.
[10] Shimomura, T., & Kumada, T. (2011). Spatial working memory load affects counting but not subitizing in enumeration. Attention, Perception, & Psychophysics, 73(6), 1694-1709.
[11] Braconier, H., & Ruiz-Valenzuela, J. (2014). Gross earning inequalities in OECD countries and major non-member economies.
[12] Anderson, J. R. (1982). Acquisition of cognitive skill. Psychological review, 89(4), 369.
[13] Domingos, A., & de Lisboa, N. APRENDIZAGEM DE CONCEITOS MATEMÁTICOS AVANÇADOS: O CONCEITO DE DERIVADA.
[14] Gaber, D., & Schlimm, D. (2015). Basic mathematical cognition. Wiley Interdisciplinary Reviews: Cognitive Science, 6(4), 355-369.
[15] Núñez, R. E., & Sweetser, E. (2006). With the future behind them: Convergent evidence from Aymara language and gesture in the crosslinguistic comparison of spatial construals of time. Cognitive science, 30(3), 401-450. doi:10.1207/s15516709cog0000_62
[16] Boroditsky, L., & Gaby, A. (2010). Remembrances of times East: absolute spatial representations of time in an Australian aboriginal community. Psychological Science, 21(11), 1635-1639.
[17] Bluedorn, A. C., & Standifer, R. L. (2006). Time and the temporal imagination. Academy of Management Learning & Education, 5(2), 196-206.
[18] Meredith, M. (2011). The fate of Africa: A history of the continent since independence. Hachette UK.
[19] Carl Zimmer (2018) Neanderthals, the World’s First Misunderstood. The New York Times.
[20] Herrmann, E., Hare, B., Call, J., & Tomasello, M. (2010). Differences in the cognitive skills of bonobos and chimpanzees. PloS one, 5(8), e12438.
[21] http://www.sciencedirect.com/science/article/pii/S0195669802001191
[22] https://cage.ugent.be/geometry/Theses/19/ekuijken.pdf
[23] http://www.sciencedirect.com/science/article/pii/0097316582900061
[24] Ehrig, H., & Mahr, B. (1985). Fundamentals of Algebraic Specification 1: Equations and Initial Semantics (Monographs in Theoretical Computer Science. An EATCS Series) (Softcover reprint of the original 1st ed. 1985 ed.). Springer.
[25] Ehrig, H., Ehrig, K., Prange, U., & Taentzer, G. (2009). Fundamentals of Algebraic Graph Transformation (Monographs in Theoretical Computer Science. An EATCS Series) (Softcover reprint of hardcover 1st ed. 2006 ed.). Springer.
[26] Stevin, S., Alexandria, D. O., & Girard, A. (2013). L’Arithmetiqve de Simon Stevin de Brvges - Primary Source Edition (French Edition). Nabu Press.
[27] HORMANN, J. O. S. E. (1956). UEBER JACOB BERNOULLIS BEITRAGE ZUR INFINITESIMALMATHEMATIK (MONOGRAPHIES DE L’ENSEIGNMENT MATHEMATIQUE NO. 3). INSTITUT DE MATHEMATIQUES; UNIVERSITE, GENEVE.
[28] Teresa Lucca, Ana M. (2013). Blog de matemáticas y TIC’S. Recuperado de https://matematics.wordpress.com/2013/12/09/rafael-bombelli/
[29] Penrose Roger (2007). El camino a la realidad. Barcelona: DEBATE.
[30] Conway, J. H. & Guy, R. K. (1996). Euler's Wonderful Relation. The Book of Numbers. New York: Springer-Verlag.